21

Розділ 1. Фізико-хімічні основи молекулярної біології

All science is either physics or stamp collection.

E. Rutherford

Незважаючи на високу складність живих систем, в основі їх функціонування лежать такі самі закони фізики, які виконуються для неживої природи – і жодних інших. Сьогодні таке тведження може здаватися банальним, але саме воно є базовим для сучасної парадігми молекулярної біології. Цей розділ має на меті нагадати деякі найбільш важливі фізичні закономірності, без розуміння яких неможливо розглядати принципи структурної організації біологічних макромолекул та взаємодії між ними.

Енергетика взаємодії між атомами та молекулами Вільна енергія

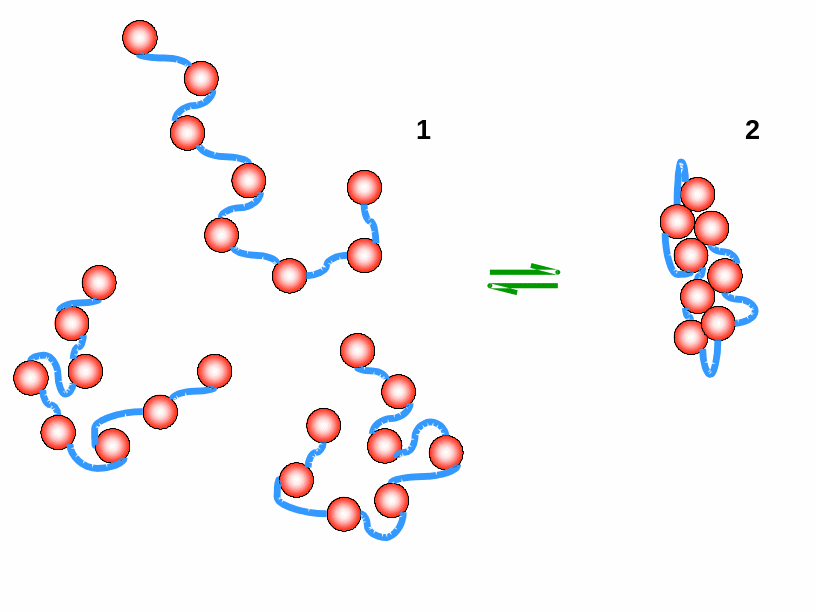Рис. 1.1. Клубок (1) та компактний стан (2) полімерного ланцюга.

Розглянемо спрощену модель полімерного ланцюга: мономерні елементи, зображені як червоні кульки на рис.1.1, що з’єднані гнучкими перемичками. Нехай мономери при цьому є інертними – не здатними до взаємодій між собою. Просторова форма – конформація – такого ланцюга буде визначатися лише конфігурацією перемичок. Внаслідок теплового руху ланцюг буде постійно змінювати свою конформацію, тобто буде реалізована так звана форма невпорядкованого клубка. На рис. 1.1 цей стан невпорядкованого клубка зображено як стан 1 ліворуч (представлено кілька з великого числа W₁ можливих конформацій). Певний компактний стан 2 (праворуч) може бути реалізований значно меншою кількістю W₂ конформацій перемичок. Відношення імовірності f₂ знайти ланцюг у стані 2 до ймовірності f₁ стану 1 (константа рівноваги K між станами 2 та 1), очевидно, визначається відношенням кількості відповідних конформацій:

.

Оскільки W₂ << W₁, рівновага зсунута ліворуч – у бік клубка. Отже, за інших однакових умов, імовірність знайти будь-яку систему в певному стані визначається числом мікростанів (конфігурацій системи), якими цей стан реалізується. Чим більшим є число мікростанів (у нашому прикладі W₁ та W₂), тим менш впорядкованим є даний стан системи: зрозуміло, що ступінь впорядкованості значно зростає для стану 2.

Нехай тепер мономери здатні взаємодіяти один із одним таким чином, що при утворенні контакту між ними в оточуюче середовище виділяється тепло (знижується внутрішня енергія нашої системи). Як відомо з термодинаміки, усі процеси, за інших однакових умов, відбуваються у напрямку виділення тепла. Імовірність певного стану системи визначається відношенням ентальпії H (величина, яка за умов постійного тиску та об’єму є еквівалентною до внутрішньої енергії системи) до середньої кінетичної енергії теплового руху k_BT (k_B – константа Больцмана (Ludwig Boltzmann), Т – абсолютна температура). А саме, імовірність є пропорційною до величини : менше значення ентальпії відповідає зростанню ймовірності (принцип Больцмана). Якщо зниження ентальпії при компактизації ланцюга є значним, то це може змінити конформаційну рівновагу на користь стану 2. Таким чином, у більш загальному вигляді маємо тепер записати:

або, позначивши S = k_BlnW і G = H – TS,

_(1.1)

де ΔG = G₂ – G₁.

Ми щойно отримали дуже важливе співвідношення, яке має універсальне значення. У рівн. 1.1 величина S, що залежить від числа мікростанів, є мірою невпорядкованості системи і називається ентропією. Величина

, (1.2)

яка була введена фундатором термодинаміки Гіббсом (Josiah Willard Gibbs), називається вільною енергією. Саме вона у загальному випадку визначає імовірність перебування системи у певному стані і, відповідно, напрям, у якому відбувається той чи інший процес. Наступні твердження, які базуються на рівн. 1.1-1.2, виконуються для будь-яких систем, в тому числі, і повною мірою, для біологічних та молекулярно-біологічних:

• Зміна стану системи відбувається у напрямку зниження вільної енергії, або: процес може відбуватися тільки тоді, коли він супроводжується зниженням вільної енергії.

• Рівноважний стан, що може бути стабільним скільки завгодно довго, відповідає мінімуму вільної енергії.

• Зміна вільної енергії залежить від двох внесків: зміна ентальпії (внутрішньої енергії), яка супроводжується виділенням/поглинанням тепла; зміна ентропії, що характеризує зростання впорядкованості/невпорядкованості у системі.

При цьому величина ентропійного внеску зростає з температурою (рівн. 1.2), тобто за високих температур переважними завжди стають менш впорядковані стани.

Слід зробити також кілька інших важливих зауважень:

• Вільна енергія є величиною відносною: має сенс тільки різниця між вільними енергіями різних станів тієї самої системи.

• Різниця між вільними енергіями двох станів системи вказує тільки на напрям перетворення одного стану на інший і нічого не каже про те, наскільки швидко і яким шляхом буде відбуватися цей процес. Інакше кажучи, стан з меншою величиною вільної енергії неодмінно має бути реалізованим, але може виявитися, що на це потрібен дуже великий час, і тому практично даний процес не спостерігається.

• Енергія взаємодії між елементами системи (атомами, молекулами) не обов’язково залежить тільки від ентальпійної складової, як у простому прикладі, що його ілюструє рис.1.1. У більш складних системах, як буде показано нижче, вільна енергія взаємодій може мати суттєву ентропійну складову, або навіть залежати тільки від ентропійних ефектів.

Рівновага утворення комплексів молекул у розчині

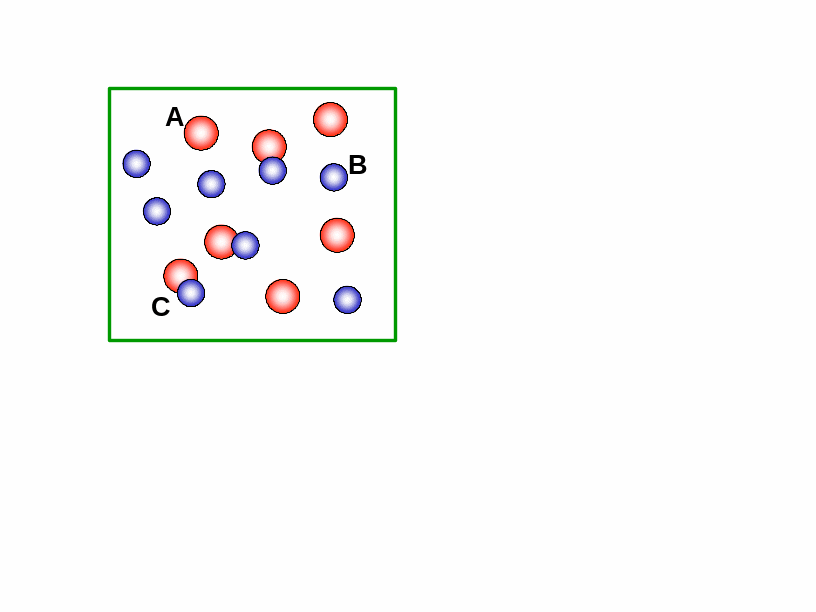Рис. 1.2. Взаємодія між молекулами А і В з утворенням комплексу С.

Перш ніж перейти до розгляду типів взаємодій між атомами та молекулами, розглянемо ще один приклад рівноваги у простій, але важливій для молекулярної біології системі. У розчині певного об’єму знаходяться молекули двох типів (А і В), які здатні утворити між собою комплекс С (рис.1.2):

(1.3)

(літерою K тут знову позначена константа рівноваги, в цьому випадку – для процесу утворення/дисоціації комплексів). Ентропійна частина вільної енергії кожного компонента містить складову, яка залежить від концентрації. Наприклад, вільну енергію G_A компонента А (що її в цьому випадку називають також хімічним потенціалом) можна записати як

, (1.4)

де – стандартна вільна енергія; R – універсальна газова стала, яка є константою Больцмана у перерахунку на моль речовини: R = k_BTN_AV, N_AV – число Авогадро (Amedeo Avogadro); квадратними дужками позначена молярна концентрація А. Зміст рівн. 1.4 дуже простий: є вільною енергією компонента А при його концентарції 1 М; зростання концентрації призводить до зниження ентропії (чим більше молекул, тим менше доступних місць розташування для кожної з них, тобто меншим є число мікростанів, – порівн. з визначенням ентропії вище) – тобто до зростання вільної енергії. Записавши аналогічні вирази для компонентів В і С, знайдемо різницю між правою та лівою частинами рівн. 1.3 ΔG = G_C – G_A – G_B:

_{, (1.5)}

де ΔG⁰ – різниця між відповідними стандартними вільними енергіями, [A] і [B] –концентрації відповідних вільних компонентів у дисоційованому стані. Процес зміни концентрацій у системі буде продовжуватись до моменту досягнення рівноваги – такого співвідношення між концентраціями, коли вільна енергія комплексу буде дорівнювати сумарній енергії вільних компонентів А і В, і ΔG = 0. (Можна показати, що загальна вільна енергія розчину буде мінімальною, коли різниця ΔG між правою і лівою частинами рівн. 1.3 дорівнює нулю.) Оскільки ΔG⁰ – це константа, яка залежить від природи компонентів, співвідношення концентрацій під логарифмом у рівн. 1.5 також є константним за рівноважних умов. Саме це співвідношення і є в даному прикладі константою рівноваги, яка залежить тільки від різниці стандартних вільних енергій:

_{. (1.6)}

Таким чином, якщо при утворенні комплексу вільна енергія знижується (ΔG⁰ < 0), це сприяє взаємодії між компонентами. У випадку, що розглядається, константу K називають також константою асоціації або константою зв'язування, а величину ΔG⁰, відповідно, стандартною вільною енергією зв'язування. Обидві константні величини є мірою спорідненості компонентів, що утворюють комплекс: чим більш негативною є енергія зв'язування (чим більше енергетично вигідних взаємодій реалізується між компонентами), тим вище значення K, і тим більш стабільним є комплекс. Слід також зауважити, що ефективність утворення комплексу, під якою можна розуміти, наприклад, частку компонента А у складі комплексу – [C]/([C]+[A]), залежить від концентрації компонентів. Рівн. 1.6 є однією з форм запису відомого закону діючих мас, або принципу Ле Шател’є (Henry Le Chatelier), згідно якого додавання у систему одного з компонентів зсуває рівновагу в протилежний бік.

Рівняння 1.3 може означати також рівняння хімічної реакції, коли, внаслідок перебудови ковалентних зв’язків (див. нижче) у молекулах А і В, утворюється нова молекула С. Тоді усі наступні рівняння та висновки з них також зберігають свою силу. У цьому випадку, знову, знак зміни стандартної вільної енергії вказує на напрям, у якому відбувається хімічна реакція. Варто підкреслити ще раз: усі хімічні реакції в живих системах відбуваються у напрямку зниження вільної енергії. Тут може виникнути запитання: якщо, наприклад, вільна енергія знижується при руйнуванні молекули С на А і В, але клітина має потребу саме у молекулі С, чи можливий синтез С? Відповідь є однозначною: синтез С із молекул А і В є неможливим. Але можна використати “обхідний” шлях: спочатку хімічно модифікувати одну з молекул (наприклад, утворити молекулу А'), і тоді може виявитися, що утворення С із А' та В супроводжується зниженням вільної енергії, тобто є можливим. Повернемося до обговорення цього питання у розділі 2.