5.5 Способы, группирования данных. Методы установления вида закона распределения.

Графически интервальный вариационный ряд можно представать в виде гистограммы (рис. ). На каждом интервале группирования как на основании строится прямоугольный столбец, высота которого равна либо числу результатов, попавших в j-тый интервал группирования nj, либо nj/n , либо nj/(n+x). Гистограмма является статистическим аналогом функции плотности распределения и позволяет судить о виде закона распределения. Соответствие вида гистограммы фактическому распределению зависит от числа интервалов группирования т. Если число интервалов m слишком велико, то гистограмма сильно изрезана, имеет провалы из-за малого числа точек, попавших в некоторые интервалы, ее вид будет значительно зависеть от случайностей экспериментальных данных (рис.а).

Рас.

Если число интервалов мало, то будут сглаживаться некоторые важные особенности распределения (рис.б). Очевидно, что должно существовать некоторое оптимальное число интервалов группирования, при котором гистограмма имеет плавный характер без разрывов и в то же время отражает особенности распределения. Рекомендации различных авторов по выбору числа интервалов группирования на основе анализа литературы приведены в табл.

Автор	Рекоменд. ф-ла
Старджес	m=3,3lg n+1
Брукс и Каррузерс	m=5lg n
Хайнхольд Гаеде
Таушанов и Тонева	m=4lg n

Приведенные рекомендации определяют число интервалов группирования в зависимости только от числа измерений n и не учитывают вид закона распределения. Однако для описания, например, островершинного распределения нужны более мелкие интервалы, чем для описания равномерного. Следовательно, величина m должна зависеть от вида распределения. Один из путей учета вида распределения - выбор интервалов такой ширины, чтобы число попаданий значении результатов измерений в них было одинаковым. В этом случае автоматически в областях с высокой плотностью значений будут более узкие интервалы. Однако в подавляющем большинстве случаев группирование производится с интервалами одинаковой ширины. В этом случае величина m должна быть функцией не только n, но и какой-либо характеристики вида закона распределения. Целесообразно выполнять расчёт m по следующему выражению

где  - контрэксцесс, характеризующий вид распределения; n – число измерений. Значения контрэксцесса для различных видов закона распределения приводятся в табл.

Полную информацию об их значениях можно получить в книге Новицкого П.В. о которой мы уже говорили.

На основе анализа наиболее часто встречающихся распределений при исследовании метрологических характеристик средств измерения можно сказать, что

(14)

Для точных расчётов значение m следует уточнить путем последовательных приближений.

Если из теории или из опыта известно, что распределение результатов измерения должно быть симметричным, то значение m необходимо округлить в большую сторону до ближайшего нечетного числа. Нечетное m обязательно при исследовании погрешностей, поскольку законы распределения погрешностей, как правило, симметричны.

Таким образом, для ориентировочного расчёта значения m следует воспользоваться выражениями (14), после чего выполнить группирование данных. Для точного определения вида закона распределения следует уточнить значение контрэксцесса по таблице и повторить группирование.

Ориентировочное суждение о виде закона распределения, как было указано, можно сделать по виду гистограммы. Гистограмму рекомендуется строить следующим образом. На ось измеряемой величины x наносят центр распределения (рис.) По формулам (14) приближенно оценивают число интервалов группирования. Затем определяют ширину интервала группирования; для этого диапазон значений результатов измерений (без промахов) делят на число интервалов группирования т. Первый интервал наносят на график так, чтобы центр распределения лежал в середине этого интервала. Так рекомендуется поступать потому, что в большинстве измерительных задач распределение результатов измерения является симметричным и одномодальным.

Симметрично располагают остальные интервалы группирования слева и справа относительно центрального интервала. Построение столбцов гистограммы производится в соответствие с предыдущими рекомендациями. По виду гистограммы в случае, показанном на рис.а закон распределения скорее всего нормальный, а в случае, показанном на рис. б, -равномерный. Однако такое определенное суждение можно высказать далеко не всегда. Часто возможны весьма широкие альтернативы.

Оценку вида закона распределения можно провести также по числовым характеристикам. Это более сложный способ, который ,однако, даёт более точные результаты.

Значения контрэксцесса для различных видов распределения.

Рис а

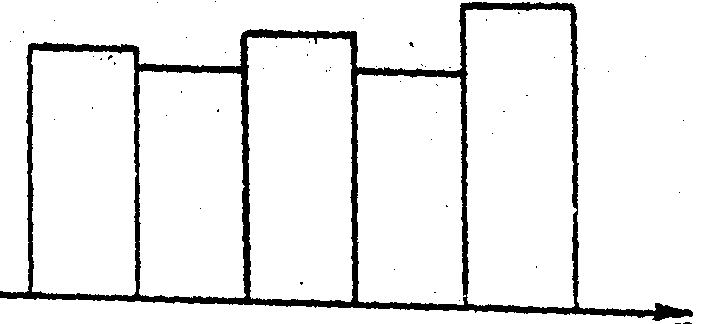
Рис б