9. Закон больших чисел. Предельные теоремы теории вероятностей.

Обозначим через S_n=₁+…+_n частичную сумму первых n элементов пос-ледовательности случайных величин  ₁, ₂,… . Пусть E_n существует при любом n, тогда для последовательности ₁,₂,… выполнен закон больших чисел (ЗБЧ), если при

Если случайные величины  ₁, ₂,…попарно независимы, одинаково рас-пределены, имеют математическое ожидание a и ограниченную дисперсию  ²<C (C=const), тогда выполнен ЗБЧ в форме Чебышёва

Неравенство даёт оценку того, что среднее арифметическое случайных вели-чин отклонится от математического ожидания по абсолютной величине бо-лее,чем на  .

Если случайная величина ξ имеет конечную дисперсию, то при любом ε>0 справедливо неравенство Чебышёва:

P{| ξ -Eξ|≥ε}≤Dξ/ε²

Для оценки вероятности отклонения частоты появления события от его вероятности можно использовать теорему Бернулли:

Пусть S_n=₁+…+_n, где  ₁, ₂,… независимые одинаково распределённые случайные величины со средним значением a и дисперсией  ²< . Тогда вы-полнена центральная предельная теорема (ЦПТ), т.е. для любого веществен-ного x имеет место сходимость

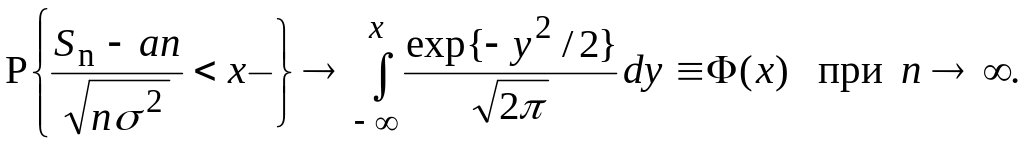
Следствием ЦПТ является интегральная теорема Муавра-Лапласа:

Здесь m – число появлений события А в n независимых испытаниях по схеме Бернулли с вероятностью p (0<p<1) для любых a и b, a < b.

На ней основана приближенная формула

которая используется при p1/2 и при сравнительно больших =np (обычно при >9), а при малых значениях   приближение Пуассона

Для функций нормального распределения и распределения Пуассона имеются таблицы.

Пример 1. Вероятность выхода из строя изделия за время испытаний на надёжность равна 0,09. Какова вероятность того, что за время испытаний 100 изделий выйдут из строя не более 10 изделий.

Решение. Согласно теореме Муавра-Лапласа имеем

.

По условию задачи n=100, p=0.09, q=(1-p)=0.91, a=0, b=10. Подставляя эти значения и определяя по таблице значения функции , получаем P{0≤m≤10}≈Ф₀(0.35)Ф₀(3.14)=Ф₀(0.35)+Ф₀(3.14)=0.1368+0.4991=0.6359.

Пример 2. Определить количество испытаний, которое нужно провести, чтобы с вероятностью не менее 0.9 можно было утверждать, что отклонение частоты появления события от его вероятности P=0.8 было бы не более 0.05?

Решение. Воспользуемся неравенством из теоремы Бернулли:

По условию задачи нужно найти n такое, что 1-pq/nε²=0.9, отсюда, подстав-ляя значения p,q и ε, находим значение n=640.

Пример 3. По каналу связи передано 10000 символов. Вероятность иска-жений каждого символа помехами р=0.001. Действие помех на каждый сим-вол происходит независимо. Какова вероятность, что при передаче будет не более 15 искажений?

Решение. По условию задачи имеем n=10000, p=0,001, q=(1-p)=0,999. Поскольку np=10, то применяем формулу

где k=15. (1,58)=₀(1,58)+0,5=0,943. Следовательно,

Варианты заданий.

1. Вероятность появления события в одном опыте p=0,003. Определить веро-ятность того, что в 1000 опытах событие появится не более четырёх раз.

2. Телефонная станция обслуживает 100 абонентов. Вероятность того, что за время t поступит один вызов, равна 0,002. Определить вероятность того, что за время t поступит не более двух вызовов.

3. Вероятность того, что прибор за время испытаний выйдет из строя, равна 0,8. Определить вероятность того, что за время испытаний 100 приборов не менее 70 из них выйдут из строя.

4. Какое наименьшее число испытаний нужно произвести для того, чтобы с вероятностью, не меньшей 0,9 частота отклонялась от вероятности p=0,5 не больше, чем на 0,01?

5. Дисперсия каждой из 800 независимых случайных величин менее 9. Како-ва верхняя граница абсолютной величины отклонения средней арифмети-ческой этих величин от средней арифметической их математических ожи-даний, если вероятность этого отклонения превышает 0,997

6. Вероятность появления события в одном опыте равна 0,4. С какой вероят-ностью можно утверждать, что частота этого события при 100 опытах бу-дет лежать в пределах от 0,2 до 0,5?

7. Определить количество испытаний, которое нужно произвести, чтобы с вероятностью не менее 0,99 можно было бы утверждать, что отклонение частоты появления события от его вероятности p=0,7 было бы не более 0,01.

8. Вероятность наличия зазубрин на брусках, заготовленных для обточки, равна 0,2. Оценить вероятность того, что в партии из 1000 брусков откло-нение числа пригодных от 800 не превышает 5%.

9. Вероятность появления события в одном опыте равна 0,002. Определить вероятность того, что в 1000 опытах событие появится не менее двух раз.

10. Вероятность выпуска сверла повышенной хрупкости (брак) равна 0,02. Свёрла укладываются в коробку по 100 штук. Чему равна вероятность того, что: а) в коробке не окажется бракованных свёрл; б) число брако-ванных свёрл окажется не более 2?

11. Вероятность любого абонента позвонить на коммутатор в течение часа равна 0,01. Телефонная станция обслуживает 200 абонентов. Какова ве-роятность того, что в течение часа позвонят не менее трёх абонентов?

12. Игральную кость бросают 120 раз. Определить вероятность того, что чис-ло выпадений 5 очков будет находиться между 15 и 27.

13. Вероятность брака при изготовлении некоторых деталей равна 0,02. Опре-делить вероятность того, что среди взятых 1000 штук деталей окажется не более 25 бракованных.

14. Вероятность выхода изделий из строя за время испытаний на надёжность равна 0,05. Какова вероятность того, что за время испытания 90 изделий выйдут из строя менее 5 изделий?

15. Вероятность получить бракованное изделие равна 0,002. Найти вероят-ность того, что среди 500 изделий будет меньше 5 бракованных.

16. Известно, что вероятность выпуска сверла повышенной хрупкости (брак) равна 0,02. Свёрла укладывают в коробку. Сколько их нужно туда поло-жить, чтобы с вероятностью, не меньшей 0,9, в ней было не менее 100 исправных?

17. Вероятность попадания в цель при одном выстреле равна 0,004. Опреде-лить вероятность того, что при 500 выстрелах будет больше 5 попаданий.

18. В передаваемой по каналу связи последовательности знаков, образующих сообщение, любой знак из-за помех независимо искажается с вероят-ностью 0,2. Передано 10000 знаков. Какова вероятность того, что в приня-той последовательности будет от 2000 до 2100 искажений?

19. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты от его вероят-ности можно ожидать с вероятностью 0,92 при 5000 испытаниях.

20. Сколько раз нужно бросить монету, чтобы с вероятностью 0,6 можно бы-ло ожидать, что отклонение частоты появления герба от вероятности p=0,5 окажется по абсолютной величине не более 0,01?

21. Вероятность того, что деталь не стандартна, равна 0,2. Найти вероятность того, что среди случайно отобранных 400 деталей частота появления нес-тандартной детали отклонится от вероятности по абсолютной величине не более чем на 0,03.

22. Вероятность попадания в цель при одном выстреле равна 0,8. Определить вероятность того, что при 300 выстрелах число попаданий будет заключе-но между 200 и 250.

23. Вероятность брака при изготовлении некоторых деталей равна 0,002. Оп-ределить вероятность того, что при изготовлении 1000 деталей будет не меньше 5 бракованных.

24. Вероятность появления события в отдельном опыте равна 0,7. Опреде-лить, начиная с какого числа n независимых испытаний вероятность нера-венства {|m/n-0,7|<0,1} будет больше, чем 0,38.

25. Вероятность выхода изделия из строя за время испытаний равна 0,06. Ка-кова вероятность того, что за время испытаний 90 изделий выйдут из строя менее 5 изделий?

ЛИТЕРАТУРА

1. Боровков А.А. Теория вероятностей.—М.:Наука,1986.

2. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. –М.: Наука, 1983.

3. Вентцель Е.С. Теория вероятностей.—М.:Высш. шк., 1999.

4. Гнеденко Б.В. Курс теории вероятностей.—М.: Наука, 1988.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.—М.: Высш. шк.,1998.

6. Коваленко И.Н., Филипова А.А. Теория вероятностей и математическая статистика.—М.: Высш. шк.,1973.

7. Печенкин В.А.,Тескин О.И. и др. Теория вероятностей.—М.: Изд-во МГТУ им. Н.Э.Баумана,1998.

8. Сборник задач по математике для втузов. Т.3. Теория вероятностей и математическая статистика/ Под. ред. Ефимова А.В.—М.: Наука, 1990.

9. Ширяев А.Н. Вероятность.—М.:Наука, 1980.

Труфанов Виктор Александрович,

доцент кафедры МАиМ АмГУ

Методические указания по типовому расчёту по курсу “Теория вероятнос-тей” для студентов всех специальностей

_______________________________________________________

Изд-во АмГУ. Подписано к печати . Формат 60х84/16. Усл. печ. л. , уч.-изд. л. . Тираж 100 экз. Заказ .

45