
Нормальность распределенияε.
Для нахождения ассиметрии:
Ϭɣ1= →
→
[ɣ]<1,5 Ϭɣ1→Ho.
[ɣ]>2 Ϭɣ1→H1.
Ϭɣ1= 0,292265
Для 1,5: 0,438398;для 2: 0,584531, отсюда следует, что ɣ2 =Но.
Между 1,5 и 2 находится зона неопределенности (т.е. нельзя принять или отклонить).
Для нахождения эксцеза:
Ϭɣ2=
[ɣ +Ϭ/(n+1)]Ϭɣ2<1,5 Ϭɣ2→Ho
[ɣ +Ϭ/(n+1)]Ϭɣ2<2 Ϭɣ2→H1
Для 1,5: 0,818036; для 2: 1,090714, отсюда следует, что ɣ1 ɣ2 находится в зоне неопределенности.
Между 1,5 и 2 также находится зона неопределенности.
Распределение ε будет нормальным, если в обоих тестах выбирается гипотеза Но, во всех остальных распределение нормальным назвать нельзя.
Прогноз.
Для прогноза возьмем 1дополнительное наблюдение из следующего месяца(первый день).
Rt=a+ b *Dt. Подставив нужные значения (вместо Dt подставляем Dp)по этой формуле
Найдем прогноз. Прогноз составит: -0,0106.
Вывод: из теста Голдфелда-Квандта видно, что дисперсии случайных отклонений постоянны (остатки гомоскедастичны). Это означает, что при каждом конкретном наблюдении случайное отклонение может быть различным, однако не должно быть причин, вызывающих большую ошибку. Статистика Дарбина-Уотсона показала отсутствие автокорреляции, значит наблюдаемые значения случайных отклонений независимы друг от друга. Из результатов тестирования выполнения предпосылок регрессионного анализа можно сделать вывод, что предпосылки регрессионного анализа выполняются, следовательно, оценки имеют желательные свойства: состоятельности, несмещенности, эффективности.
Приложение.
1.Исходные данные.
Дата торгов |
P цена |
I индекс |
Rt |
Dt |
01.03.12 |
100,25 |
1723,57 |
|
|
02.03.12 |
101,6 |
1726,73 |
0,0134663 |
0,0018334 |
05.03.12 |
102,3 |
1752,17 |
0,0068898 |
0,0147331 |
06.03.12 |
97,37 |
1676,48 |
-0,0481916 |
-0,0431979 |
24.05.12 |
81,44 |
1287,43 |
0,0354736 |
0,0183028 |
25.05.12 |
79,87 |
1272,69 |
-0,0192780 |
-0,0114492 |
28.05.12 |
80,37 |
1277,15 |
0,0062602 |
0,0035044 |
29.05.12 |
84,14 |
1307,03 |
0,0469081 |
0,0233958 |
30.05.12 |
82,38 |
1273,26 |
-0,0209175 |
-0,0258372 |
31.05.12 |
81,69 |
1242,43 |
-0,0083758 |
-0,0242134 |
2. Вывод итогов.
Регрессионная статистика |
|
|
|
|||||
Множественный R |
0,881634469 |
|
|
|
||||
R-квадрат |
0,777279337 |
|
|
|
||||
Нормированный R-квадрат |
0,773687068 |
|
|
|
||||
Стандартная ошибка |
0,010394767 |
|
|
|
||||
Наблюдения |
64 |
|
|
|
||||
Дисперсионный анализ |
|
|
|
|
||||
|
df |
SS |
MS |
F |
Значимость F |
|||
Регрессия |
1 |
0,02338 |
0,023379639 |
216,3756082 |
6,87633E-22 |
|||
Остаток |
62 |
0,006699 |
0,000108051 |
|
|
|||
Итого |
63 |
0,030079 |
|
|
|
|||
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
Y-пересечение |
0,002488818 |
0,001351 |
1,842122869 |
0,070240557 |
-0,000211912 |
0,00519 |
-0,00021 |
0,00519 |
Переменная X 1 |
1,100371274 |
0,074806 |
14,70971136 |
6,87633E-22 |
0,950836673 |
1,24991 |
0,950837 |
1,249906 |
прогноз |
-0,010601245 |
|
|
|
|
|
|
|
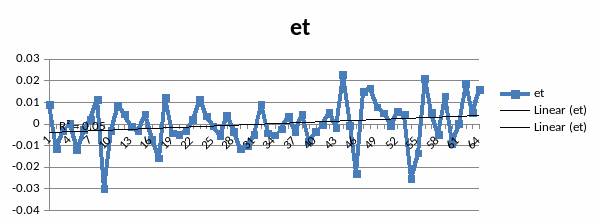
3.DW== 2,07. [0;4]
ВЫВОД ОСТАТКА |
|
|
|
|
||
|
|
|
|
|
|
|
Наблюдение |
t |
et |
et-1 |
(et-et-1)^2 |
|
|
1 |
0,004506243 |
0,00896 |
|
|
|
|
2 |
0,018700644 |
-0,01181 |
0,008960091 |
0,000431433 |
|
|
3 |
-0,045044869 |
-0,00315 |
-0,01181088 |
7,50676E-05 |
|
|
4 |
0,00296796 |
0,000216 |
-0,00314672 |
1,13064E-05 |
|
|
5 |
0,03139537 |
-0,01205 |
0,000215772 |
0,000150363 |
|
|
6 |
-0,002082024 |
-0,00274 |
-0,01204648 |
8,66346E-05 |
|
|
57 |
0,00547703 |
0,005139 |
0,020996855 |
0,000251465 |
|
|
58 |
-0,045442807 |
-0,00491 |
0,0051392 |
0,000100933 |
|
|
59 |
0,022628653 |
0,012845 |
-0,00490735 |
0,000315145 |
|
|
60 |
-0,010109515 |
-0,00917 |
0,012844965 |
0,000484592 |
|
|
61 |
0,006344947 |
-8,5E-05 |
-0,00916848 |
8,25137E-05 |
|
|
62 |
0,028232931 |
0,018675 |
-8,4774E-05 |
0,000351934 |
|
|
63 |
-0,025941698 |
0,005024 |
0,018675119 |
0,000186348 |
|
|
64 |
-0,024154952 |
0,015779 |
0,00502418 |
0,000115669 |
|
|
|
|
|
0,015779132 |
0,000248981 |
|
|
|
|
|
|
0,01368041 |
|
|

Рср= (n-2)= 41,33333
Ϭр2= = 11,05556.
p>[pср-1,96 ]→εслуч
pср-1,96 ]= 34,81635
H0:E-не случ.
H1:E-случ.
