38. Асимптоты графика функции. Схема исследования функции.

При исследовании поведения функции на бесконечности, т. е. при х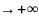 и при х или вблизи точек разрыва второго рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют асимптотами

Существует три вида асимптот: вертикальные, горизонтальные и наклонные.

Определение 1. Прямая x=x₀ называется вертикальной асимптотой графика функции у=f(х), если хотя бы одно из предельных значений или равно + или — .

Например, график функции y=f(x)=1/x (рис. 1) имеет вертикальную асимптоту x = 0, так как f(x) при x 0+ и f(x при 0-

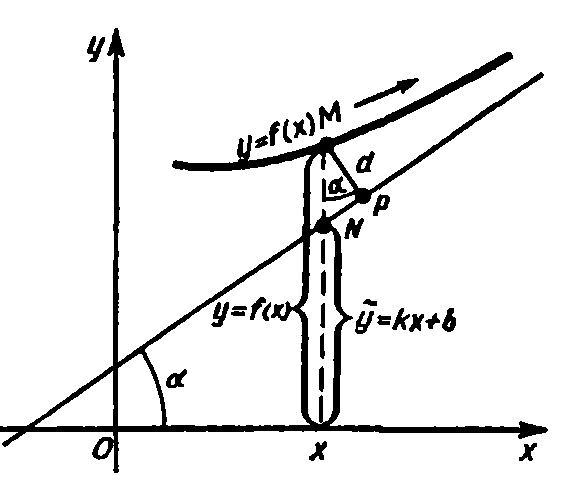
рис.1 рис.2

Определение 2. Прямая у = А называется горизонтальной асимптотой графика функции y=f(x) при x (x ), если .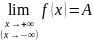

Например, график рассмотренной выше функции у=1/х имеет горизонтальную асимптоту у=0 при x и при x , так как 1/x 0 при x и при x

Определение 3. Прямая y = kx + b (к ) называется наклонной асимптотой графика функции y=f(x) при x (x ),, если функцию f(x) можно представить в виде

f(x)=kx+b+ (x) (1)

где (х) при x (x ).

Выясним геометрический смысл наклонной асимптоты. Для определенности рассмотрим случай, когда x (случай x рассматривается аналогично).

Пусть М(х; у)—точка графика функции у=f(х), и пусть прямая y=kx + b является наклонной асимптотой графика функции при х . Текущую ординату точки на асимптоте обозначим через у(сверху у ставится волнистая линия), точку на асимптоте — через N(x; у(сверху у ставится волнистая линия)) (рис.2). Тогда |MN| = |y—y (сверху у ставится волнистая линия)| = |f(x)—(kx + b)| = | (х)| при x . Опустим из точки М перпендикуляр МР на асимптоту. Расстояние d от точки М до асимптоты равно IMPI = IMN| cos , где — угол между асимптотой и осью Ох и, следовательно, =0.

Таким образом, расстояние от точки М{х; у) графика функции до асимптоты стремится к нулю при x 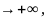т. е. график функции неограниченно приближается к асимптоте при x .

Рассмотрим способ отыскания наклонной асимптоты, т. е. способ определения чисел k и b в уравнении асимптоты. Разделив равенство (1) на х и перейдя к пределу при x , получаем

так как и Итак, k= . (2)

Далее, из соотношения (1) имеем 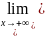[f(x)-kx]= =b

Таким образом, b= [f(x)-kx]. (3)

Мы доказали, что если прямая у(сверху у ставится волнистая линия) = кх + b является наклонной асимптотой, то числа k и b находятся по формулам (2) и (3). Обратно, если оба предела (2) и (3) существуют, причем k , то прямая у = kх + b является наклонной асимптотой графика функции y=f(x) при x . В самом деле, полагая и используя равенство (3), получаем, что =0. Следовательно, справедливо равенство f(x)=kx+b+ (x), где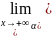 (x)=0, т.е. прямая y(сверху у ставится волнистая линия) = kx + b является наклонной асимптотой графика функции при x .

Заканчивая рассмотрение наклонной асимптоты, сформулируем полученный результат в виде теоремы. Теорема 1. Для того чтобы график функции y=f(x) имел при x (x ) наклонную асимптоту y =kx+b, необходимо и достаточно, чтобы существовали два предела

и

Целесообразно искать асимптоты в следующем порядке: 1) вертикальные асимптоты; 2) горизонтальные асимптоты; 3) наклонные асимптоты.

Схема исследования графика функции. В данном пункте познакомимся с примерной схемой, по которой целесообразно исследовать поведение функции и строить ее график. Изучение заданной функции и построение ее графика целесообразно проводить в следующем порядке:

1) найти область определения функции;

2) найти точки пересечения графика функции с осями координат;

3) найти асимптоты;

4) найти точки возможного экстремума;

5) найти критические точки;

6) с помощью вспомогательного рисунка исследовать знак первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремума и точки перегиба;

7) построить график

При этом в начале исследования полезно проверить, является данная функция четной или нечетной, чтобы при построении использовать симметрию графика относительно оси ординат или начала координат.

[если на экзамене в этом вопросе будет дополнительно «Достаточное условие экстремума» то пишем это: Установим достаточное условие существования локальнoго экстремума.

Теорема 2 (достаточное условие локального экстремума). Пусть функция f(x) дифференцируема в некоторой -окрестности точки х₀. Тогда, если f ’(x)>0 (f'(x)<0) для всех х из (х₀ - , х₀), а f'(x)< 0 (f’ (x) > 0) для всех х из (х₀, х₀ + ), то в точке х₀ функция f(x) имеет локальный максимум (минимум), если же f ‘(x) во всей окрестности точки х₀ имеет один и тот же знак, то в точке х₀ локального экстремума нет.

Другими словами, если f'(x) при переходе через точку х₀ меняет знак с + на —, то х₀ — точка локального максимума, если f' (х) в точке x₀ меняет знак с — на +, то х₀ — точка локального минимума, если же знак f'(х) в точке х₀ не изменяется, то в точке х₀ экстремума не существует.

Доказательство. Пусть f'(х) при переходе через точку х₀ меняет знак с + на — и пусть х ( х₀ - , х₀). Применим формулу Лагранжа к функции f(x) на отрезке [х, х₀]. Получаем f(x₀)-f(x) =f '(c)(x₀-x), x .

Так как f'(х)>0 на (х₀ - , х₀), тоf'(с)>0 и, кроме того, х₀ —х>0, следовательно, f(x₀)-f(x)> 0 или f(x₀)>f(x). (1)

Рассмотрим теперь интервал справа от точки х₀, т. е. х (х₀, х₀ + ). Применим формулу Лагранжа к функции f(x) на отрезке [х₀, х]. Получаем f(x)-f(x₀)=f'(c)(x-x_o), c (x₀, х).

Так как f'(x)<0 на (х₀, х₀ + ), то f'(с)<0 и, кроме того, х —х₀>0, следовательно, f(x)-f(x₀) или f(x₀) >f(x). (2)

Из неравенств (1) и (2) следует, что в рассматриваемой окрестности точки х₀ выполняется неравенство f(x)<f(x₀) при x x₀, а это означает, что в точке х₀ функция f(х) имеет локальный максимум.

Осталось рассмотреть случай, когда f'(x) не меняет знака.

Пустьf'(x)> 0 в некоторой окрестности (х₀ – ), тогда, по теореме o признакe монотонности, функция f(x) не убывает на (х₀ – ), т.е. для любых х<х₀ выполняется неравенство f(x) < f(x₀), а для любых х>х₀ — неравенство f(x)>f(x₀). Это означает, что точка х₀ не является точкой локального экстремума, т. е. при переходе через нее в данном случае не сохраняется знак разности f(x)—f(x₀) в окрестности этой точки.

Замечание. Теорема 2 остается справедливой, если функция f(х) в самой точке х₀ не дифференцируема, а только непрерывна. Примером такой функции является f(x) = |x|, которая в точке х = 0 непрерывна, но не дифференцируема. ]