34. Понятие монотонности функции. Признак монотонности функции.

Определение 1: Функции называется возрастающей [убывающей] на множестве , если для любых значений аргумента из выполняется условие .

Определение 2: Промежутки области определения, на которых функция возрастает или убывает, называются промежутками монотонности функции.

Определение 3: Функция называется возрастающей [убывающей], если для любых значений аргумента из выполняется условие .

Определение 4: Возрастающие и убывающие функции называются монотонными.

Теорема. Если функция f(x) дифференцируема на интервале (а, b) и f’(x)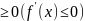 на (а, b), то функция f(x) не убывает (не возрастает) на (а, b).

Доказательство. Для определенности рассмотрим случайf’(x)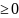 . Пусть х₁ и х₂—две произвольные точки из (а, b) и x₁<x₂; тогда на отрезке [ x_1, x₂] выполняются все условия теоремы Лагранжа, согласно которой имеем

f(x₂)-f(x₁)=f ’(c)(x₂-x₁), c .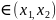

Согласно условию f ‘(c) , 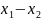>0, поэтому f(x₂)-f(x₁) или f(x₂)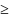 f(x₁), т. е. функция f(x) не убывает на (a, b).

Доказательство для случая f’(x)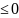 аналогичное.

Замечание. Точно так же можно доказать, что если f’(x)>0(<0) на (a, b), то f(x)возрастает (убывает) на (а, b)

35. Экстремум функции. Необходимое условие экстремума

Определение. Точка х₀ называется точкой строго локального максимума (минимума) функции f(х), еcли для всех х из некоторой -окрестности точки х₀ выполняется неравенство f(x)<f(x₀) (f(x)>f(x₀)) при x x₀ (рис. 1).

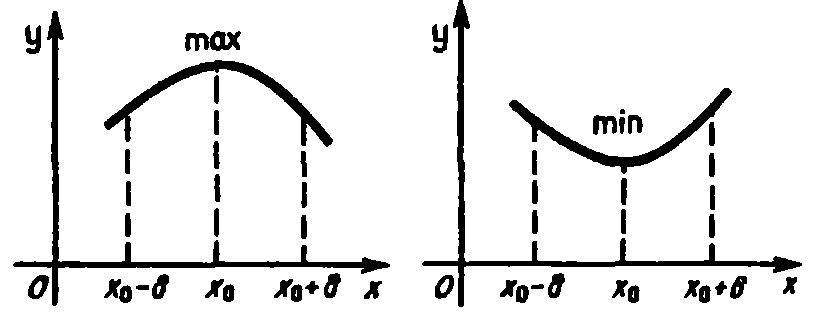
рис. 1

Локальный максимум (max) и локальный минимум (min) объединяются общим названием локальный экстремум.

Из определения следует, что понятие экстремума носит локальный характер в том смысле, что в случае экстремума неравенство f(x)<f(x₀) (f(x)>f(x₀)) не обязано выполняться для всех значении х в области определения функции, а должно выполняться лишь в некоторой окрестности точки x₀. Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то локального минимума.

Теорема 1 (необходимое условие локального экстремума). Если функция f(x) имеет в точке х₀ локальный экстремум и дифференцируема в этой точке, то f'(x₀) = 0.

Доказательство. Так как в точке х₀ функция f(x) имеет локальный экстремум, то существует такой интервал (х₀ — , х₀ + ), в котором значение f(x₀) является наибольшим (наименьшим) среди всех других значений этой функции. Тогда, по теореме Ферма, производная функции в точке х₀ равна нулю, т. е. f'(x₀) = 0.

Теорема 1 имеет следующий геометрический смысл. Если х₁, х₂, и х₃ — точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные параллельны оси Ох (рис.2).

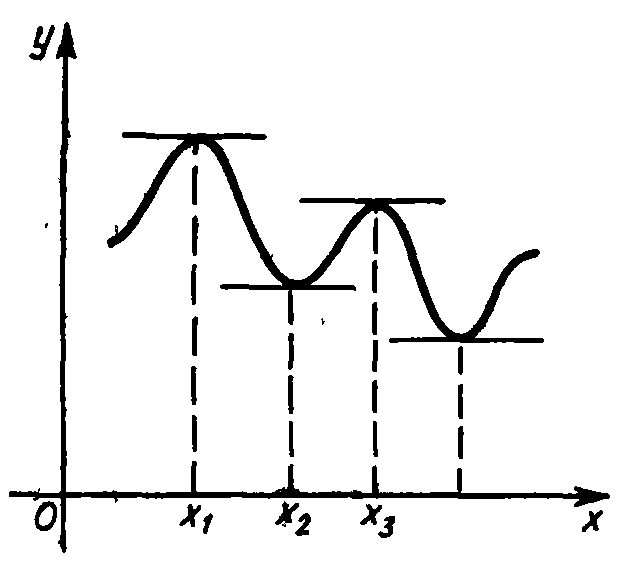
рис.2

Иногда такие точки называют стационарными; мы будем называть их точками возможного экстремума. Если точка х₀ — точка возможного экстремума, т. е. f'(х₀) = 0, то она может и не быть точкой локального максимума (минимума). Например, если f(x) = x³, то f'(х) = Зх² = 0 при x = 0, но тем не менее в точке х=0 нет локального экстремума (рис 2). Поэтому мы их и назвали точками возможного экстремума, а условие f'(x₀)=0 является лишь необходимым.

[если на экзамене в этом вопросе будет дополнительно «Достаточное условие экстремума» то пишем это: Установим достаточное условие существования локальнoго экстремума.

Теорема 2 (достаточное условие локального экстремума). Пусть функция f(x) дифференцируема в некоторой -окрестности точки х₀. Тогда, если f ’(x)>0 (f'(x)<0) для всех х из (х₀ - , х₀), а f'(x)< 0 (f’ (x) > 0) для всех х из (х₀, х₀ + ), то в точке х₀ функция f(x) имеет локальный максимум (минимум), если же f ‘(x) во всей 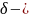окрестности точки х₀ имеет один и тот же знак, то в точке х₀ локального экстремума нет.

Другими словами, если f'(x) при переходе через точку х₀ меняет знак с + на —, то х₀ — точка локального максимума, если f' (х) в точке x₀ меняет знак с — на +, то х₀ — точка локального минимума, если же знак f'(х) в точке х₀ не изменяется, то в точке х₀ экстремума не существует.

Доказательство. Пусть f'(х) при переходе через точку х₀ меняет знак с + на — и пусть х ( х₀ - , х₀). Применим формулу Лагранжа к функции f(x) на отрезке [х, х₀]. Получаем f(x₀)-f(x) =f '(c)(x₀-x), x .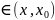

Так какf'(х)>0 на (х₀ - , х₀), тоf'(с)>0 и, кроме того, х₀ —х>0, следовательно, f(x₀)-f(x)> 0 или f(x₀)>f(x). (1)

Рассмотрим теперь интервал справа от точки х₀, т. е. х (х₀, х₀ + ). Применим формулу Лагранжа к функции f(x) на отрезке [х₀, х]. Получаем f(x)-f(x₀)=f'(c)(x-x_o), c (x₀, х).

Так как f'(x)<0 на (х₀, х₀ + ), то f'(с)<0 и, кроме того, х —х₀>0, следовательно, f(x)-f(x₀)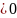 или f(x₀) >f(x). (2)

Из неравенств (1) и (2) следует, что в рассматриваемой окрестности точки х₀ выполняется неравенство f(x)<f(x₀) при x x₀, а это означает, что в точке х₀ функция f(х) имеет локальный максимум.

Осталось рассмотреть случай, когда f'(x) не меняет знака.

Пустьf'(x)> 0 в некоторой окрестности (х₀ –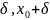 ), тогда, по теореме o признакe монотонности, функция f(x) не убывает на (х₀ – ), т.е. для любых х<х₀ выполняется неравенство f(x) < f(x₀), а для любых х>х₀ — неравенство f(x)>f(x₀). Это означает, что точка х₀ не является точкой локального экстремума, т. е. при переходе через нее в данном случае не сохраняется знак разности f(x)—f(x₀) в окрестности этой точки.

Замечание. Теорема 2 остается справедливой, если функция f(х) в самой точке х₀ не дифференцируема, а только непрерывна. Примером такой функции является f(x) = |x|, которая в точке х = 0 непрерывна, но не дифференцируема. ]