28. Параметрическое задание функции.

Пусть даны две функции х = (t), y = Y(t) (1)

одной независимой переменной t, определенные и непрерывные в одном и том же промежутке. Если x = (t) строго монотонна, то обратная функция t = Ф(х) однозначна, также непрерывна и строго монотонна. Поэтому y можно рассматривать как функцию, зависящую от переменной x посредством переменной t, называемой параметром: y=Y[Ф(x)]

В этом случае говорят, что функция y=f(x) задана параметрически с помощью уравнений (1). Отметим, что функция Y[Ф(x)] непрерывна в силу теоремы о непрерывности сложной функции.

Дифференцирование функции, заданной параметрически.

Предположим теперь, что функции х = (t) и y = Y(t) имеют производные, причем ‘(t) на некотором промежутке. Из последнего неравенства вытекает строгая монотонность функции х= (t) и, следовательно, однозначность обратной функции t = Ф(х). По теореме о производной обратной функции, функция Ф(x) имеет производную Ф’(х)=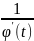 , а по теореме о производной сложной функции, функция у =Y [Ф(x)] имеет производную y_x’=Y’(Ф(x)) Ф’(x)

Следовательно, y_x’= или, короче, y_x’= .

Таким образом, мы доказали, что производная функции, представленной параметрически, выражается формулой

y_x’= .

29. Теорема Лагранжа. Формула конечных приращений

Теорема Лагранжа: Пусть на отрезке [а, b] определена функция f(x), причем: 1) f(x) непрерывна на [а, b]; 2) f(x) дифференцируема на (а, b). Тогда существует точка c (a, b) такая, что справедлива формула

Замечание 1. Равенство f(b)-f(a)=f'(c)(b-a), а<с<b (1)

называется формулой Лагранжа, или формулой конечных приращений.

Замечание 2. Так как точка с лежит между точками а и b, то можно записать

c = a + (b-a), 0< <1.

Здесь (b — а) — часть длины отрезка [а, b]. Учитывая это, формулу Лагранжа можно записать в виде

f(b)-f(a)=f'(a+ {b-a))(b-a), 0< <l.

Замечание 3. Если положить а = х, b=х + х, то получим f(x + x)-f(x)=f'(x + x) x, 0< <1. Такая запись формулы Лагранжа часто бывает удобнее, чем запись (1).

Теорема Лагранжа лежит в основе доказательства многих формул и теорем анализа.

30. Раскрытие неопределенности вида ( ). Теорема Лопиталя

Следующая теорема дает правило раскрытия данной неопределенности.

Теорема Лопиталя. Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки а, за исключением, быть может, самой точки а. Пусть, далее, = в указанной окрестности точки а. Тогда, если существует предел отношения производных (конечный или бесконечный), то существует и предел , причем справедлива формула

.

Раскрытие неопределенности вида ( )

Для этой неопределенности справедливо утверждение, аналогичное теореме Лопиталя, а именно: если в формулировке теоремы заменить требование на условие то теорема останется справедливой.

Другие виды неопределенностей и их раскрытие.

Неопределенности вида 0* и , как известно, можно свести к неопределенностям вида и , а затем раскрыть с помощью правила Лопиталя.

И наконец, рассмотрим неопределенности вида 0°, . Такие неопределенности имеют место при рассмотрении функций y=f(x)^g(x), если при х а функция f(x) стремится соответственно к 0, 1 и , а g(x)—соответственно к 0, и 0. Эти неопределенности с помощью тождества f(x)^g(x)=e^g(x)lnf(x) сводятся к неопределенности вида 0* , которая уже рассмотрена.