20.Производная степенной функции. Производная функции y=xn , показатель n которой является целым положительным числом, выражается формулой y’=n*xn-1 .
Доказательство: используя формулу бинома Ньютона, можно записать:
=[
]-
=
+
*
+
… +
.
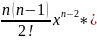Таким
образом, при
имеем
+… +
.
Так
как
… ,
то y’=
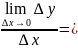nxn-1
.
Производная
показательной функции. Производная
функции y= ax
(0<a
)выражается
формулой
y’ = ax lna
Доказательство:
показательная функции y= ax
является
обратной для логарифмической функции
x=
.
Так как x’(y)
=
.
То в силу теоремы о производной обратной
функции и известного из элементарной
математики соотношения
=
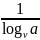получаем y’(x)
=
=
ax
lna.
Следcтвие:
если y=
,
то y=(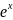
)’=
.
Производные тригонометрических функций.
Производная функции y=sinx выражается формулой y’=cosx
Доказательство:
Имеем
Таким образом, при
=
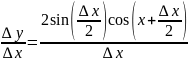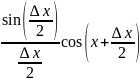
=1
(первый замечательный предел), а
=
cosx
в силу непрерывности функции cosx,
то y’=
cosx.
производная функции y= cosx выражается формулой y’= - sinx.
Доказательство:
Имеем
Таким образом, при
= -
Т.к.
в силу непрерывности функции sinx,
то y
’
= - sinx..
3)
производная функции y=tgx
выражается формулой y’=
(x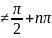
)
Доказательство:
т.к. tgx
= sinx/
cosx,
по теореме [(u
)’,
(u/v)]
получим
y’=
=
=
,
следовательно y’=
4)производная
функции y=ctgx
выражается формулой y’=
(x
)
Доказательство: т.к. ctgx= cosx/ sinx, то аналогично предыдущему имеем
y’=
=
=
,
следовательно y’=
21.
Производная логарифмической функции.
Производная функции y =
(О < а
1)
выражается формулой
y’=
Доказательство:
имеем
Таким
образом, при
=
или
=
.
Положив
имеем
=
(второй замечательный предел), а т.к.
логарифмическая функция является
непрерывной, то y’=
=
]=
.
Следствие:
если y’
=
.
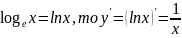Производная обратно тригонометрической функции.
1)
производная функции y=arcsinx
выражается формулой y’=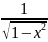
(
)
Доказательство:
функция y=arcsinx
является обратной для функции x=siny.
Т.к. x’(y)=cosy,
то по теореме о производной обратной
функции, получаем y’(x)=
=
=
.
Корень
взят со знаком плюс, потому что
положителен
на интервале
.
Учитывая, что siny=x,
окончательно получаем y’(x)
=
2)Производная функции y=arccosx выражается формулой y’(x) = -
Доказательство: аналогично предыдущему.
3)Производная
функции y=arctgx
выражается формулой y’(x)=
Доказательство:
функция y=arctgx
является обратной для функции x=tgx.
Т.к. x’(y)=
, то y’(x)=
=
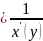Но
=1+
, следовательно y’(x)=
.
4)Производная функции y=arcсtgx выражается формулой y’(x)= - .
Доказательство аналогично предыдущему.
22. Обратная функция. Производная обратной функции.
Пусть
функция y=f(x)
удовлетворяет условиям теоремы об
обратной функции и функция x=
является для нее обратной. Тогда имеет
место след. теорема.
Если
функция y=f(x)
имеет в точке x0
производную
f’(x0)
,то
обратная функция x=
также имеет в соответствующей точке y0
= f(x0)
производную причем
.
Доказательство.
Дадим аргументу у обратной функции x=
некоторое
приращение
в
точке
.
Функция x=
получит
некоторое приращение
обратной функции,
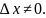следовательно, можно записать
Перейдем
в этом равенстве к пределу при
.
Так как обратная функция x=
непрерывна
в точке y0,,то
о
.
Но при
предел
правой части равенства существует и
равен 1/f’(x0,),
следовательно, существует предел и
левой части равенства, который по
определению равен
.
Таким образом
, получаем
23. Сложная функция и ее дифференцирования.
Теорема:
если функция x=
t0
,
а
функция y=f{x) имеет производную в
соответствующей точке х0
= ф(t0),
то сложная функция f[
]имеет
производную в точке t0
и имеет место следующая формула: y’(t0)
= f’(t0)
(1)
Доказательство.
Так как функция
y=f(x)
предполагается
дифференцируемой в точке х0, то приращение
этой функции может быть записано в виде
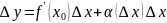(2), где
.
Разделив равенство (2)
на
t
имеем
=
+
(3). Равенство
(3) справедливо при любых достаточно
малых
Возьмем
равным
приращению функции x=
,
соответствующему приращению
t
аргумен- та t. Устремим в этом равенстве
t
к нулю. Так как, по условию, функция x=
имеет в точке
производную, то она непрерывна в этой
точке. Следовательно, по третьему
определению непрерывности функции в
точке,
при
t
. Но тогда устремится к нулю и
,
т. е. получим
(
)=
0*
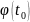=0
(4)
Из соотношения (4) следует существование предела всей правой части равенства (3) при t , равного f’(t0) . Значит, существует предел при t и левой части равенства(3), который, по определению производной, равен производной сложной функции y= f[ ]. Тем самым доказана дифференцируемость сложной функции и установлена формула (1).
Замечание. В данной теореме мы рассматривали сложную функцию, где у зависела от t через промежуточную переменную х. Возможна и более сложная зависимость — с двумя, тремя и большим числом промежуточных переменных, но правило дифференцирования остается прежним.
Так,
например, если у =f{x),
где х =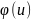
, а u=
то
производную y'{t)
следует искать по формуле
y’(t)=y’(x)x’(u)u’(v)v’(t)
(5)
Дифференциал сложной функции: dy=f’(x)dx
24. Производная степенной функции с любым показателем.
Производная
функции у=
(
—любое
вещественное число) определяется
формулой y’=
Доказательство.
Так как у=
, то lny=
.
Используя формулу (ln|f’(x)|)’=
,
получаем
=[
]’=
.
Отсюда учитывая, что у=
,
получаем формулу для производной
степенной функции: y’=
Таблица производных.
I. (С)' = 0.
II.
(
,
в частности (
)’=
-
, (
)’=
.
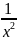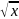III.
(
)’=
в частности (lnx)’
=
.
IV.
(
)’=
в
частности (
)’=
V. (sinx)’= cosx
VI. (cosx)’= -sinx
VII.(tgx)’=
VIII.
(ctga)’=-
IX. (arcsinx)’=
X. (arccosx)’= -
XI. (arctgx)’=
XII. (arcctgx)’= - .