Построение отклика аналогового фильтра на сигнал
Входной сигнал имеет вид:
,
.
Представим
два типовых сигнала (1-единичный скачок
(функция Хевисайда), 2-линейная функция)
и
в операторной форме:
;
.
Сигнал
представляет
собой единичный скачёк (
).
Зная, что реакцией цепи на единичный
скачёк является переходная характеристика
цепи, можем сразу записать отклик цепи
на воздействие сигналом
.
.
Отклик на воздействие сигналом будет иметь вид:
.
Теперь, зная отклики на каждый из составных сигналов, изобразим выходной сигнал.
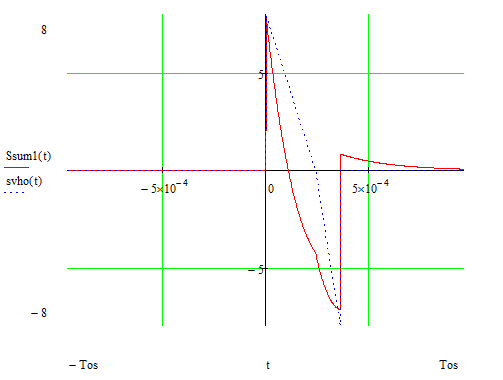
Рисунок 4.6. – Графическое представление выходного сигнала
5. Синтез цифрового фильтра методом инвариантности импульсной характеристики
5.1 Дискретизация импульсной характеристики аналогового фильтра
Для дискретизации импульсной характеристики необходимо вначале найти интервал дискретизации. Найдем, используя теорему Котельникова:
,
.
,
и
помножим импульсную характеристику на
.
Получим:
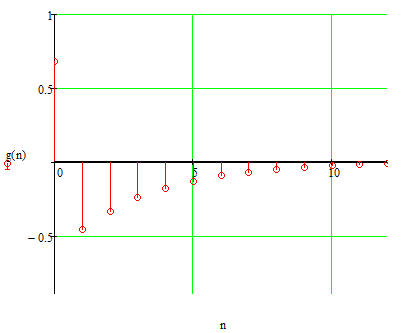
Рисунок 5.1- Дискретная импульсная характеристика.
5.2 Расчет тцф методом иих.
Для нахождения системной функций ТЦФ необходимо ограничить импульсную характеристику по пороговому критерию, определенному как десять процентов второго отсчета дискретной импульсной характеристики:
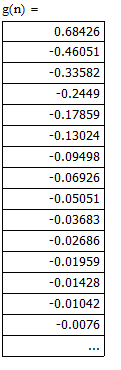
g(0) =0.68426*0.1=0.068426;
M=8;
Теперь мы можем представить системную функцию трансверсального ЦФ суммой следующего вида:
.
Трансверсальный ЦФ имеет конечную импульсную характеристику.
Исходя из системной функции нетрудно составить структурную схему ТЦФ, рисунок 5.2.
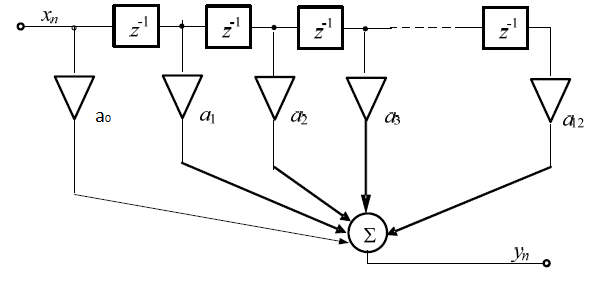
Рисунок 5.2 Структурная схема ТЦФ.
Построение частотных характеристик ТЦФ
Частотные
характеристики ТЦФ получаем из его
системной функции путем замены
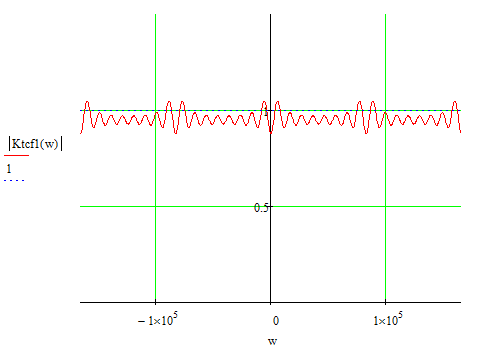
Рисунок 5.3-АЧХ трансверсального цифрового фильтра.
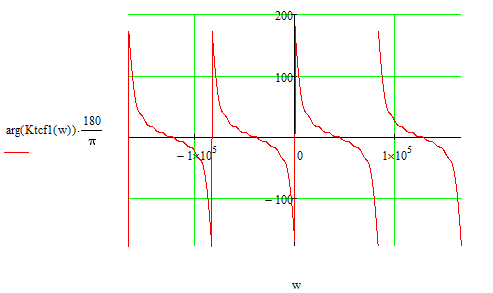
Рисунок 5.4 - ФЧХ трансверсального цифрового фильтра.
5.3. Расчет рцф методом иих.
В отличие от трансверсальных фильтров, имеющих конечную импульсную характеристику, рекурсивные фильтры имеют бесконечную импульсную характеристику, из-за этого их иногда называют фильтрами бесконечной импульсной характеристики, БИХ фильтрами. Системная функция рекурсивного цифрового фильтра определяется формулой:
,
Подставив дискретную импульсную характеристику, свернем бесконечную геометрическую прогрессию, а затем приведем управнение к каноническому виду, получим:
,
На основе системной функций запишем алгоритм работы РЦФ:
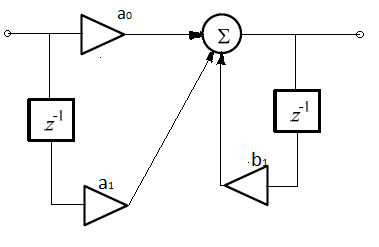
Рисунок 5.5 Структурная схема РЦФ.
Построение частотных характеристик РЦФ
Переход
от системной функций осуществим путем
замены
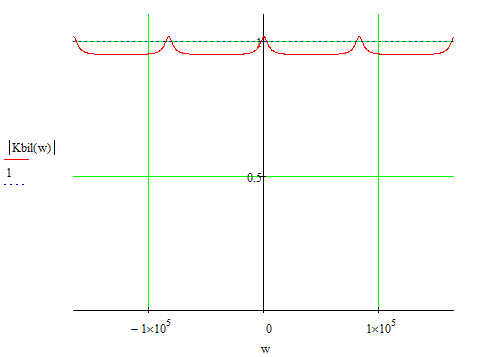
Рисунок 5.6 Амплитудно- частотная характеристика РЦФ.
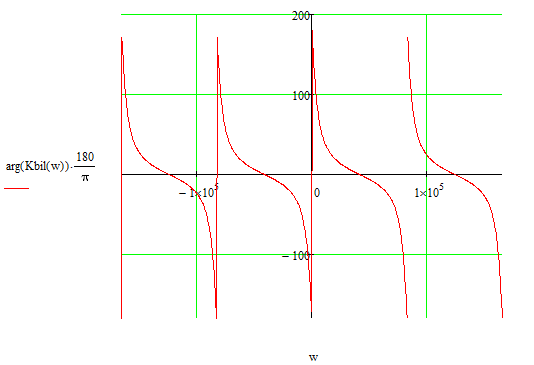
Рисунок 5.7 Фазочастотная характеристика РЦФ.
6. Синтез цифрового фильтра методом билинейного Z-преобразования
6.1 Нахождение системной функций РЦФ
Для перехода к системной функций рекурсивного фильтра, воспользуемся заменой вида:
Тогда системная функция примет вид:
6.2 Построение частотных характеристик РЦФ.
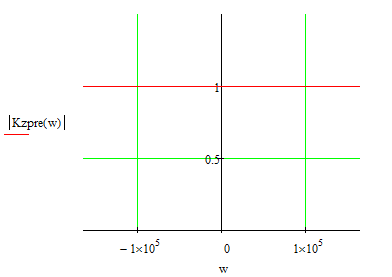
Рисунок 6.1. - Амплитудно- частотная характеристика РЦФ
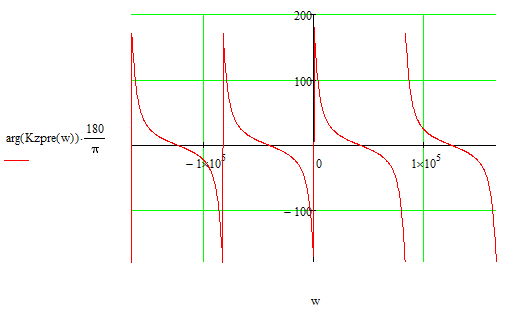
Рисунок 6.2.Фазочастотная характеристика РЦФ.
6.3 Расчет отклика ЦФ на дискретный сигнал
По алгоритму работы РЦФ построим отклик РЦФ на дискретный сигнал, полученный путем дискретизации аналогового сигнала.
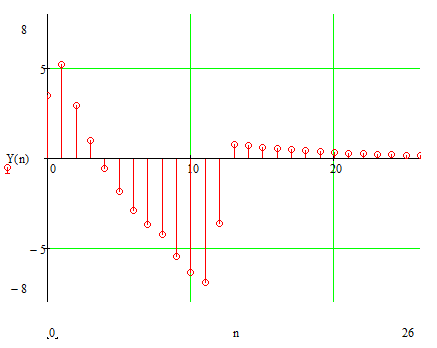
Рисунок 6.3. Отклик цифрового фильтра на дискретный сигнал
7. Выводы:
В данной курсовой работе мы получили первые навыки работы с сигналами. Работа началась с аналогового сигнала, который мы исследовали, нашли его спектр, комплексные коэффициенты ряда Фурье, а затем восстановили по Фурье. Затем этот сигнал мы пропустили через линейную цепь, рассмотрели основные принципы действия линейной цепи на аналоговый сигнал. Мы начали с дискретизаций сигнала, и нахождения его спектра, отметили что спектр дискретизированного сигнала является периодической функцией. Научились восстанавливать дискретный сигнал по Котельникову и проверили правильность этого восстановления, восстановлением по Фурье.
Мы продесткретизировали импульсную характеристику аналогового фильтра прототипа, и с использованием метода ИИХ, построили трансверсальный КИХ фильтр и рекурсивный БИХ фильтр. Также по комплексному коэффициенту передачи аналогового фильтра прототипа мы синтезировали РЦФ методом билинейного Z- преобразования.