3. Нахождение и построение коэффициентов комплексного ряда Фурье

Для восстановления аналогового сигнала с помощью комплексного ряда Фурье необходимо найти его комплексные коэффициенты. Коэффициенты определим путем дискретизации спектральной плотности аналогового сигнала:

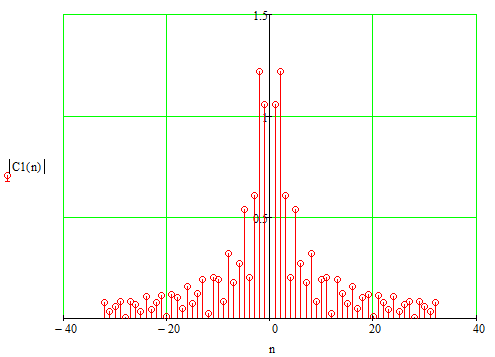
Рисунок 2.5 – Спектр коэффициентов комплексного ряда Фурье.

Для сравнения с комплексными коэффициентами ряда постоянную составляющую исходного аналогового сигнала определим отдельно. Она равна:

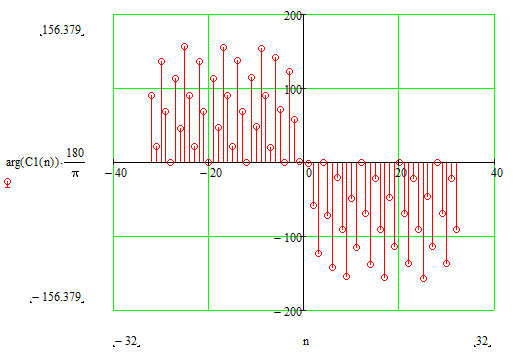
Рисунок 2.6 –Спектр фаз коэффициентов комплексного ряда Фурье.

3. Нахождение ширины спектра сигнала

Для ограничения спектра сигнала необходимо задаться пороговым

критерием. Из соображений, приведенных выше, порог определим как де-

сятую часть амплитуды второй гармоники.

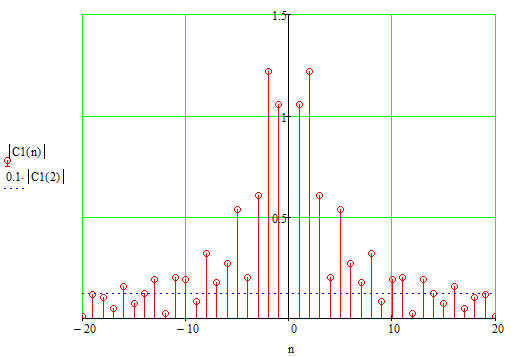
Рисунок 2.7 – Определение ширины спектра аналогового сигнала.

Из рисунка видно, что шестнадцатый коэффициент — это последний

коэффициент с амплитудой, превышающей порог, значит, сигнал будем

восстанавливать по шестнадцати гармоникам, то есть .

3. Восстановление сигнала усеченным рядом Фурье

Восстановление сигнала определяется следующей формулой:

.

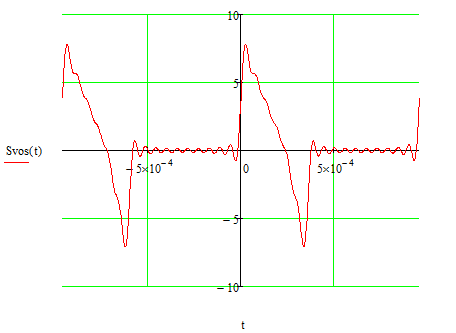
Рисунок 2.8 – Графический результат восстановления сигнала рядами Фурье.

Восстановленный сигнал имеет периодический, пульсирующий характер. Периодизация сигнала произошла из-за дискретизации спектральной плотности в частотной области, а пульсирует восстановленный сигнал из-за ограниченной шестнаднатью гармониками ширины спектра сигнала.

2. Дискретизация аналогового сигнала.

3.1 Дискретизация исходного сигнала

Прежде чем начать дискретизацию аналогового сигнала, необходимо определить параметры дискретизации:

- интервал дискретизации.

Дискретный сигнал определяется формулой .

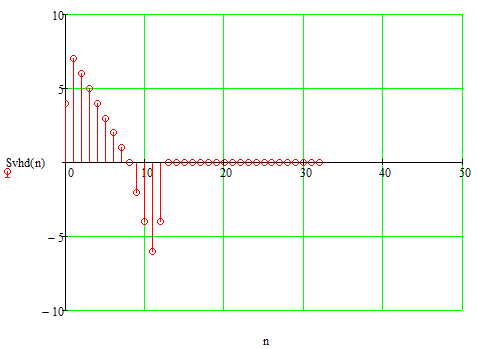
Рисунок 3.1- Дискретный сигнал.

Построение спектральной плотности дискретного сигнала.

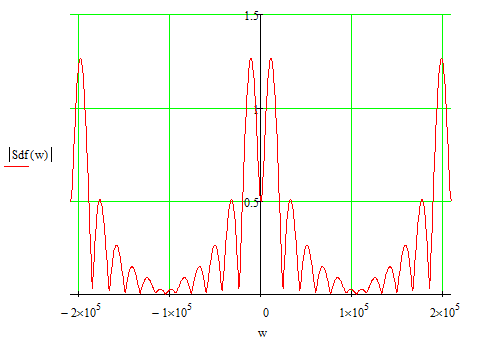
Рисунок 3.2- Спектральная плотность дискретизированного сигнала.

Из рисунка 3.2 видно, что АЧХ дискретного сигнала стала периодической функцией. Это произошло вследствие дискретизации исходного сигнала по времени.

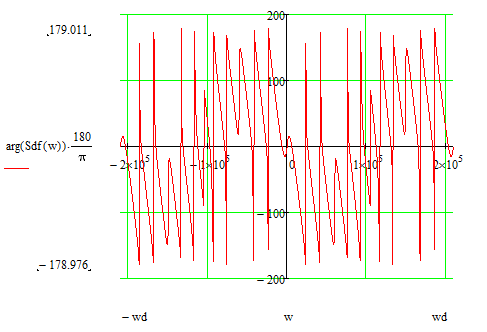
Рисунок 3.3- Фазочастотная характеристика.

3.2. Расчёт и построение спектра комплексных коэффициентов дпф

Для нахождения дискретного представления сигнала в частотной области применяем прямое дискретное преобразование Лапласа.

.

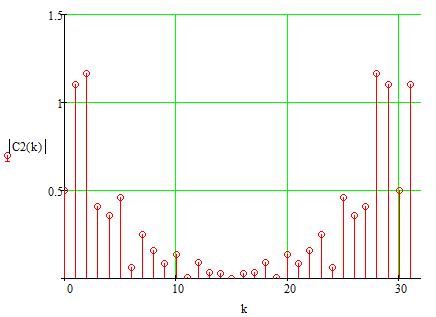
Рис. 3.4 — Спектр модулей комплексных коэффициентов ДПФ

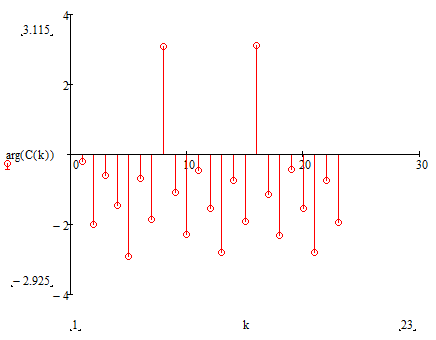
Рис. 3.5 — Спектр фаз комплексных коэффициентов ДПФ

Из графика видно, что если поменять знак индекса на противоположный, знак аргумента также инвертируется, другими словами, комплексные коэффициенты, симметричные относительно начала координат,

являются комплексно-сопряженными.

3. Восстановление аналогового сигнала

Восстановление сигнала проведём двумя способами: с помощью

теоремы Котельникова и по Фурье.

Восстановление по Фурье определяется следующей формулой:

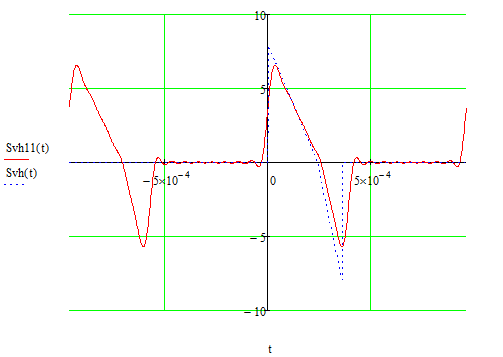
Рис. 3.6 — Сигнал, восстановленный по Фурье

Восстановление с помощью теоремы Котельникова:

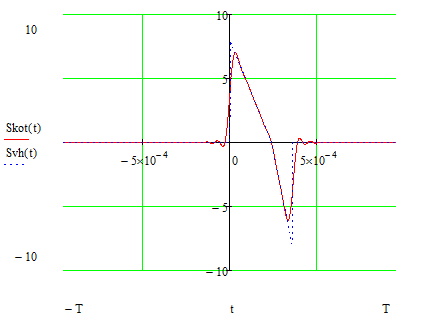
Рисунок 3.7 Сигнал, восстановленный по Котельникову.

2. Анализ аналоговой линейной электрической цепи

1. Исходные данные

Схема заданного четырехполюсника выглядит следующим образом:

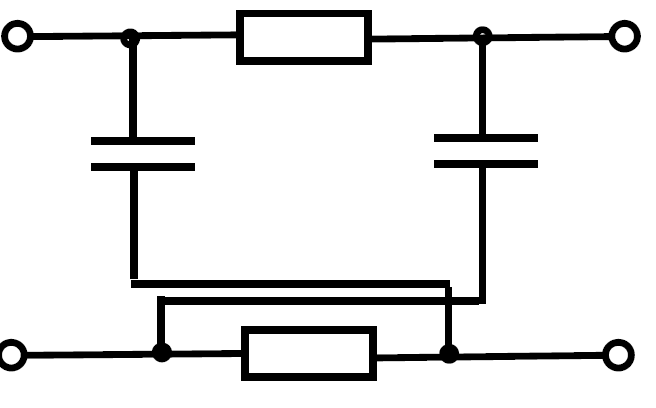
Рис.4.1 Схема исходного аналогового фильтра-прототипа

При этом известно соотношение между постоянной времени цепи и интервалом описания фрагмента сигнала : , и α = .

2. Нахождение передаточной функции аналогового фильтра

.

Построение частотных характеристик аналогового фильтра

Перейдём от операторной формы к комплексной, для этого произведём замену: . Тогда выражения для амплитудно-частотной и фазочастотной характеристик соответственно примут вид:

;

.

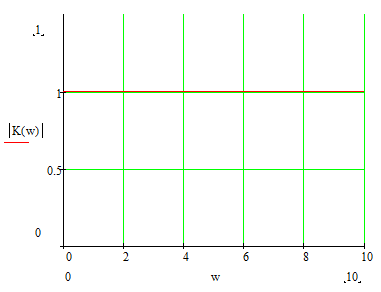
Рисунок 4.2 – График амплитудно-частотной характеристики передаточной функции цепи.

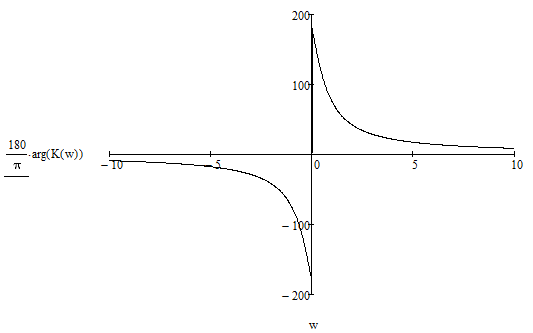
Рисунок 4.3 – График фазо-частотной характеристики передаточной функции цепи.

3. Нахождение временных характеристик аналогового фильтра

Для нахождения отклика цепи на сигнал, необходимо определить временные характеристики заданного четырехполюсника, а именно отклики на типовые составляющие исходного сигнала.

Зная выражение передаточной функции цепи, по определению найдём выражения переходной и импульсной характеристик.

;

.

Переход от оригинала к изображению будем осуществлять через теорем обращения, по которой обратное преобразование Лапласа равно сумме вычетов в особых точках, тогда:

.

;

.

Окончательно переходная характеристика выглядит:

.

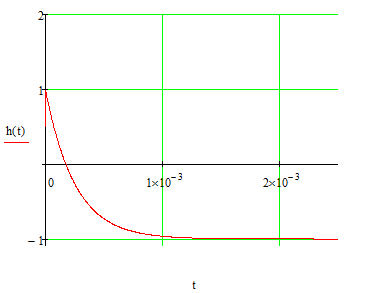
Рисунок 4.4 – Переходная характеристика цепи.

.

Так как максимальная степень числителя равна максимальной степени знаменателя брать обратное преобразование Лапласа брать напрямую нельзя. Для начала выделим целую часть из выражения передаточной функции цепи:

.

Возьмём обратное преобразование Лапласа от каждого из слагаемых в отдельности, пользуясь вышеуказанной теоремой обратимости:

;

.

Окончательный вид импульсной характеристики:

.

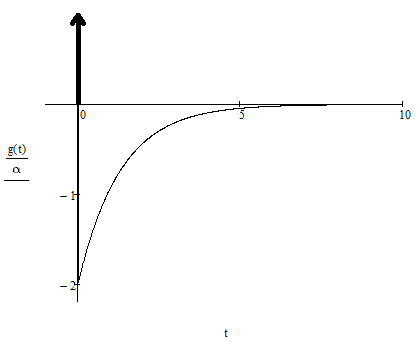
Рисунок 4.5 – Импульсная характеристика цепи.