17. Закон Био–Савара. Теорема о циркуляции

Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.

Индукцию   проводника с током можно представить как векторную сумму элементарных индукций   создаваемых отдельными участками проводника.

Закон Био–Савара определяет вклад   в магнитную индукцию   результирующего магнитного поля, создаваемый малым участком Δl проводника с током I. 

Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ₀ – магнитная постоянная. Направление вектора   определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока: 

Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле, где R – радиус кругового проводника

. Для определения направления вектора   также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.

Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользаоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.

Циркуляцией вектора   называют сумму произведений  Δl, взятую по всему контуру L: 

Теорема о циркуляции утверждает, что циркуляция вектора   магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ₀на сумму всех токов, пронизывающих контур: 

Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции.

В силу симметрии вектор   направлен по касательной   , а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению: 

откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее.

18.Явище електромагнітної індукції

Явище виникнення у провіднику електрорушійної сили при зміні магнітного поля, що пронизує площу контуру провідника, називається електромагнітною індукцією. Якщо провідник замкнений, то в ньому виникне електричний струм. Струм, що виникає у провіднику при електромагнітній індукції, називається індукційним.

Виникнення індукційного струму завжди пов'язане із зміною магнітного потоку через контур провідника. Ці зміни можуть відбуватися з різних причин, зокрема через:

– переміщення постійного магніту відносно нерухомого провідника;

– переміщення контуру відносно нерухомого магніту;

– замикання та розмикання струму в обмотці нерухомого електромагніту, розміщеного поблизу провідника;

– відносне переміщення контуру і електромагніту;

– зміну індукції магнітного поля електромагніту (виймання осердя при стало-му струмі в обмотці або зміну струму реостатом);

– зміну комутатором напрямку струму в обмотці електромагніту;

– постійний рух контуру в неоднорідному магнітному полі;

– обертальний рух контуру в однорідному магнітному полі.

Отже, індукційний струм у замкненому контурі виникає тільки тоді, коли змінюється магнітний потік, який проходить через площу, охоплену контуром.

Фарадей встановив, що напрямок індукційного струму в провіднику залежить від характеру зміни (збільшення чи зменшення) магнітного потоку через його контур. Якщо при внесенні постійного магніту в котушку стрілка гальванометра відхиляється в один бік, то при вийманні магніту вона відхиляється в протилежний бік.

Загальне правило, за допомогою якого можна визначити напрямок індукційного струму в замкненому провіднику, сформулював Е.Х. Ленц:

індукційний струм у замкненому провіднику завжди має такий напрямок, що створений цим струмом власний магнітний потік протидіє тим змінам зовнішнього магнітного потоку, які збуджують індукційний струм.

Використовуючи закон Ленца для визначення напряму індукційного струму, треба:

1) знайти причину, яка створює індукційний струм;

2) вважати, що індукційний струм протидіє цій причині, знайти напрямок його магнітного поля;

3) визначити напрямок індукційного струму за напрямком його магнітного поля.

Із закону Ленца можна встановити, що енергія індукційного струму у провіднику утворюється за рахунок тієї енергії, яка витрачається на подолання протидії магнітного поля індукційного струму.

Завдяки явищу електромагнітної індукції можна перетворити механічну енергію в електричну, а також передавати електричну енергію з одного кола в інше.

Індукційний струм   у замкненому провіднику з опором R виникає під дією  , яку можна виразити за законом Ома

.

Оскільки та сама ЕРС у провідниках з різним опором створює неоднакові струми, то для кількісної характеристики явища електромагнітної індукції зручніше користуватися величиною  , а не силою індукційного струму  .

Дослідження індукційного струму в контурах різної форми і розмірів показали, що ЕРС електромагнітної індукції   в контурі пропорційна до швидкості зміни магнітного потоку Ф через поверню, обмежену цим контуром (закон Фарадея):

.

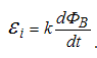ЕРС електромагнітної індукції в контурі вважають позитивною, якщо магнітний момент   відповідного їй індукційного струму утворює гострий кут з лініями магнітної індукції того поля, яке наводить цей струм (рис. 123).

Тоді для випадку, зображеного на рисунку ліворуч,  , а для зображеного праворуч — . В системі CІ 

.

Знак "–" є математичним виразом правила Ленца.

Ця формула, яка об'єднує закони Фарадея і Ленца, є математичним виразом основного закону електромагнітної індукції:

електрорушійна сила електромагнітної індукції в замкненому контурі числово дорівнює і протилежна за знаком швидкості зміні магнітного потоку крізь поверхню, обмежену контуром.

Якщо ЕРС індукції виникає при зміні магнітного потоку, який пронизує котушку з N витків, то її величина буде відповідно в N разів більшою, ніж для одного витка, тобто

.

На основі закону електромагнітної індукції можна означити одиницю магнітного потоку вебер: 1Вб – це такий магнітний потік, при зменшенні якого до нуля протягом 1с в колі, яке він пронизував, виникає ЕРС індукції в 1В.

Фарадей встановив кількісний закон електромагнітної індукції, описавши його рівнянням:

Де  — електрорушійна сила (ЕРС), яка виникає в котушці, що перебуває у змінному магнтіному полі, у вольтах,N — кількість витків у котушці,Φ — магнітний потік у веберах

Я кщо в провіднику виникає електрорушійна сила, то відповідно, індукований в ньому струм буде визначатися за законом Ома формулою,де R — опір провідника. Такий струм називається індукційним струмом

,

.

Закон електромагнітної індукції в диференціальній формі задається другим рівнянням Максвела^[1]

,

де   — напруженість електричного поля,   — магнітна індукція, c — швидкість світла у вакуумі.

Електричне поле, яке виникає при зміні магнітного поля призводить до появи електрорушійної сили.

19.Самоіндукція — явище виникнення електрорушійної сили в провіднику при зміні електричного струму в ньому. Знак електрорушійної сили завжди такий, що вона протидіє зміні сили струму. Самоіндукція призводить до скінченного часу наростання сили струму при вмиканні джерела живлення і спадання струму при розмиканні електричного кола.

Величина електрорушійної сили самоіндукції визначається за формулою

,

де   — е.р.с.,   — сила струму, L — індуктивність.

Розрахунок індуктивності контура

Явище самоіндукції виникає в провідниках зі змінним струмом, навколо яких створюється змінне магнітне поле. Власне магнітне поле контура створює магнітний потік самоіндукції   через поверхню  , що обмежена цим контуром:

де  - проекція вектора індукції магнітного поля струму на нормаль до елемента поверхні  . За законом Біо-Савара-Лапласа магнітна індукція   в точці, що знаходиться на віддалі   від елемента   контура зі струмом  , дорівнює:

звідки знаходимо

де інтегрування розповсюджується на всю довжину   контура зі струмом. Проекція вектора   на деякий напрям   запишеться у вигляді:

Підставляючи   у вираз для магнітного потоку самоіндукції, отримуємо:

де  - радіус- вектор, проведений із початку вектора   в центр елемента поверхні  .

Сила струму   в контурі не залежить від  , а   — універсальна стала, тому

або

де

Індуктивність — фізична величина, що характеризує здатність провідника нагромаджувати енергію магнітного поля, коли в ньому протікає електричний струм.

Позначається здебільшого латинською літерою L, в системі СІ вимірюється в Генрі.

Дорівнює відношенню магнітного потоку Φ через контур, визначений електричним колом, до величини струму І в колі , тобто

.

Енергія магнітного поля, створеного електричним струмом у колі, визначається формулою

.

Індуктивність залежить від форми контура.

Коефіцієнти індуктивності

У випадку кількох контурів зі струмом, як, наприклад, у випадку трансформатора, струм у кожному з кіл впливає на потік магнітного поля через інші контури.

.

Коефіцієнти   називаються коефіцієнтами індукції. Діагональні елементи   суть індуктивності i-тих контурів, а недіагональні елементи  , де   мають назву коефіцієнтів взаємної індукції. Коефіцієнти взаємної індукції симетричні відносно перестановки індексів

.

Це твердження носить назву теореми взаємності.