1.Електричне поле. Закон Кулона у векторному вигляді. Принцип суперпозиції.

1. Електричне поле, його напруженість. Принцип суперпозиції полів

Електричне поле – це матеріальна складова електромагнітного поля, яка діє на заряд, зумовлене зарядами або змінним у часі магнітним полем. Основною ознакою наявності електричного поля є те, що на будь-який заряд, внесений у це поле, діє сила.

Якщо поле створено нерухомим зарядом і в кожній точці є незмінним у часі, його називають електростатичним полем.

Головна властивість електричного поля – дія на електричні заряди з деякою силою. Таким чином, взаємодія заряджених тіл здійснюється не безпосереднім їх впливом один на одного, а через електричні полюси, що оточують заряджені тіла.

Для кількісного визначення електричного поля вводиться силова характеристика – напруженість електричного поля.

Напруженістю електричного поля називають фізичну величину, рівну відношенню сили, з яким поле діє на позитивний спробний заряд, поміщений у дану точку простору, до величини цього заряду:

Напруженість електричного поля, створюваного системою зарядів у даній точці простору, дорівнює векторній сумі напруженостей електричних полів, створюваних у тій же точці зарядами окремо:

Ця властивість електричного поля означає, що поле підкоряється принципу суперпозиції.

Відповідно до закону Кулона, напруженість електростатичного поля, створюваного точковим зарядом Q на відстані r від нього, дорівнює по модулю

Закон Кулона - це закон про взаємодії точкових електричних зарядів.

Формулювання закону: Сила взаємодії двох точкових нерухомих заряджених тіл у вакуумі спрямована вздовж прямої, що з'єднує заряди, прямо пропорційна добутку модулів зарядів і обернено пропорційна квадрату відстані між ними. 

В векторному вигляді у формулюванні Ш. Кулона закон записується таким чином:

де  F 12 - Сила, з якою заряд 1 діє на заряд 2; q _1, q ₂ - Величина зарядів; r - Радіус-вектор (вектор, спрямований від заряду 1 до заряду 2, і рівний, по модулю, відстані між зарядами - r ₁₂ ); k - Коефіцієнт пропорційності. Таким чином, закон вказує, що однойменні заряди відштовхуються (а різнойменні - притягуються).

Напруженість результуючого електричного поля системи точкових заряджених тіл визначається векторною сумою напруженостей полів окремих заряджених тіл. Цей висновок, який підтверджується експериментально, називають принципом незалежності дії електричних полів, принципом накладання, або суперпозиції.

Питання 2.Теорема Гауса і її застосування для розрахунку поля точкового заряду(площини, двох паралельних площин, сфери, кола і циліндра)

I. Розглянемо електростатичне поле, що створюється одиничним позитивним зарядом. Розмістимо його у сферу радіуса R. Визначимо потік напруженості через сферичну поверхню радіуса R.

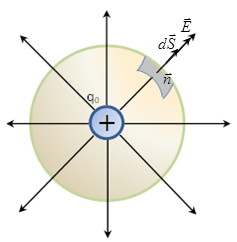Розіб’ємо поверхню S сфери на елементарні площадки ds. Нормаль до площадки ds спрямована по лінії радіуса сфери й збігається з напрямком вектора : парал ельна тому

Звідси слідує що

Тоді потік вектора Е через поверхню S буде дорівнювати сумі потоків через елементарні площадки ds і спрямовуючи ds до 0 можна записати, що

Враховуючи, що напруженість поля точкового заряду рівна

о держимо

Цей результат можна узагальнити на випадок будь-якої поверхні.

Враховуючи принцип суперпозиції можна отриманий результат застосувати до будь-якої кількості зарядів, що перебувають усередині поверхні.

ТЕОРЕМА ГАУСА:

Потік вектора напруженості Е через довільну замкнену поверхню дорівнює алгебраїчній сумі зарядів, оточених усередині цієї поверхні, діленої на ε0 (ε0 - електрична постійна)

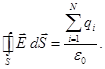
II. Застосування теореми Гауса.

Напруженість поля, створювана нескінченно протяжної однорідно зарядженої площини з поверхневою густиною заряду σ.

ПОВЕРХНЕВА ГУСТИНА ЗАРЯДУ показує, який заряд припадає на одиницю площі

Лінії напруженості Е перпендикулярні розглянутої поверхні й спрямовані від неї в обидва боки. Побудуємо циліндр із основою S, твірна якого паралельна лініям напруженості .

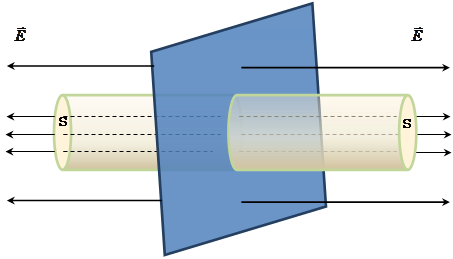
Тому що твірна циліндра паралельна Е , то потік через основу S рівний

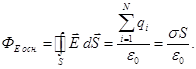
Потік через бічну поверхню циліндра дорівнює нулю, тому що Е перпендикулярна S cosα= cos90° = 0, отже,

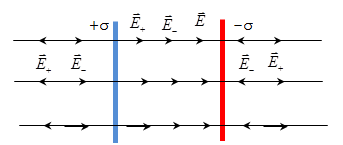
2. Напруженість поля, створювана двома паралельними нескінченно протяжними пластинами з поверхневою густиною зарядів +σ і -σ. Знайдемо поле Е, використовуючи принцип суперпозиції полів. В області між площинами

Ліворуч і праворуч від площин поля віднімаються, тому що лінії напруженості спрямовані назустріч одна одній .

3. Напруженість поля, створювана нескінченно протяжною ниткою з лінійною густиною заряду а τ.

Лінійна густина заряду показує,який заряд припадає на одиницю довжина провідника.

Потрібно визначити напруженість поля на деякій відстані r від нитки. Для цього побудуємо циліндр радіуса r і висотою h, по осі якого проходить нитка.

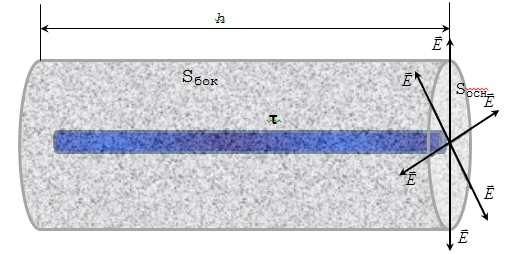
Потік через основи розглянутого циліндра дорівнює нулю, тому що Е перпендикулярна вектору S осн, отже, потік буде визначатися тільки потоком через бічну поверхню циліндра

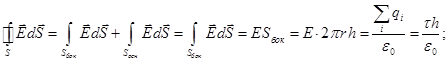
4. 4. Напруженість поля, створюваного сферичною поверхнею з поверхневою густиною заряду σ. На сфері радіуса R розподілений заряд q. Поверхнева густина заряду

Лінії напруженості спрямовані радіально, відходячи від поверхні сфера під прямим кутом. Оточуємо дану сферу сферою радіуса r і визначаємо потік напруженості Е через сферичну поверхню радіуса r.

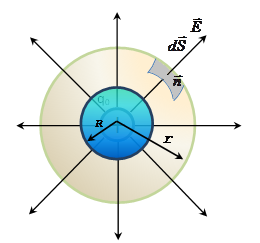
При r > R увесь заряд q попадає усередину сфери r. Тоді по теоремі Гауса

, т.к. Еn = E.

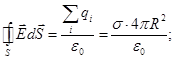
Звідси слідує.

При r < R усередині поверхні радіуса r зарядів немає й тому Е=0. На цьому засноване екранування - захист від зовнішніх електричних полів.

Висновки

Таким чином ми бачимо, що теорема Гауса дозволяє легко й швидко розраховувати поля в практично важливих випадках. Поле двох заряджених пластин являє собою поле плоского конденсатора. Поле зарядженої циліндричної поверхні здійснюється в полі циліндричного конденсатора електричного кабеля і т.д.