Выводы.

• При осуществлении НСД отбор мощности происходит путем изгиба волокна.

• Поскольку требуемое значение отведенной оптической мощности известно, то можно найти требуемый радиус изгиба, зная зависимость потерь на изгибе от радиуса.

• Существует множество теоретических исследований явления потерь на изгибе волоконных световодов. Все теоретически полученные зависимости являются приближенными, так как учет влияния всех факторов очень сложен.

• Экспериментальное исследование потерь на изгибе помогает сделать оценку реально отводимой мощности..

• Не вся потерянная на изгибе мощность может быть потом собрана и введена затем в устройство перехвата, и то, какая доля мощности все же будет введена, зависит от конструкции устройства сбора мощности.

Расчет зависимостей вероятности ошибки в канале перехвата от уровня отводимой мощности

При организации НСД к ВОЛС в распоряжении злоумышленника имеются достаточно малые объемы мощности полезного сигнала, которые он мог бы использовать для своих криминальных целей. В остальном приемное устройство злоумышленника можно рассматривать так же, как и любое другое, но с той лишь разницей, что к нему предъявляются особые требования.

В приемном устройстве злоумышленника имеются фотоприемник, преобразующий оптическую мощность падающего на него света в электрический ток, декодер, осуществляющий анализ тока фотоприемника для выделения двоичной информации, и конечное устройство, которое работает с уже принятой полезной информацией, например, отображает или сохраняет ее.

При рассмотрении современных цифровых систем передачи можно легко обозначить роль фотоприемника и декодера в более узком смысле. Любая информация, например телефонный разговор, не может быть передана по волоконному кабелю, не будучи закодированной. Вначале аналоговый сигнал кодируется в цифровую форму (последовательность двоичных символов), а потом происходит модуляция оптической мощности в волокне по какому-либо закону согласно значениям этих двоичных символов.

В современных системах связи для кодирования двоичных символов в оптических линиях в основном используется код NRZ в его модификации для волоконно-оптических систем передачи. При этом передаче двоичного символа "единица" соответствующий импульс света заданного уровня интенсивности, а передаче символа "ноль" - отсутствие импульса. Любой получатель информации хочет видеть на выходе приемного устройства восстановленную последовательность символов, которая была бы аналогична переданной. В соответствии с этим задачу, которую должно выполнять фотоприемное устройство, можно описать следующим образом.

Импульс света, соответствующий передаче символа "единица", имеет длительность Т и уровень мощности Р, а импульс, соответствующий передаче символа "ноль", имеет такую же длительность и уровень Р. Декодирующее устройство наблюдает за уровнем принимаемой оптической мощности, анализирует эту информацию и выносит решение о том, какой символ ("0" или "1" был в этот момент передан). Присутствие аддитивных шумовых полей на выходе фотодетектора, аддитивных шумов в цепях, предшествующих декодирующему устройству, вызывает ошибки в двоичных знаках при вынесении окончательного решения.

Одной из процедур вынесенного решения, на основе которой функционируют декодирующие устройства, является процедура сравнения принятого сигнала с некоторым заданным порогом. Чтобы выбрать наиболее подходящие моменты времени для произведения такого сравнения, в фотоприемных устройствах применяются специальные схемы фазовой синхронизации. Когда подходящий момент выбран, декодер измеряет уровень сигнала на входе, берет заданный уровень порога и сравнивает их. Если уровень сигнала превышает уровень порога, то выносится решение о приеме двоичной единицы, а если сигнал меньше порогового уровня - декодер констатирует прием нуля.

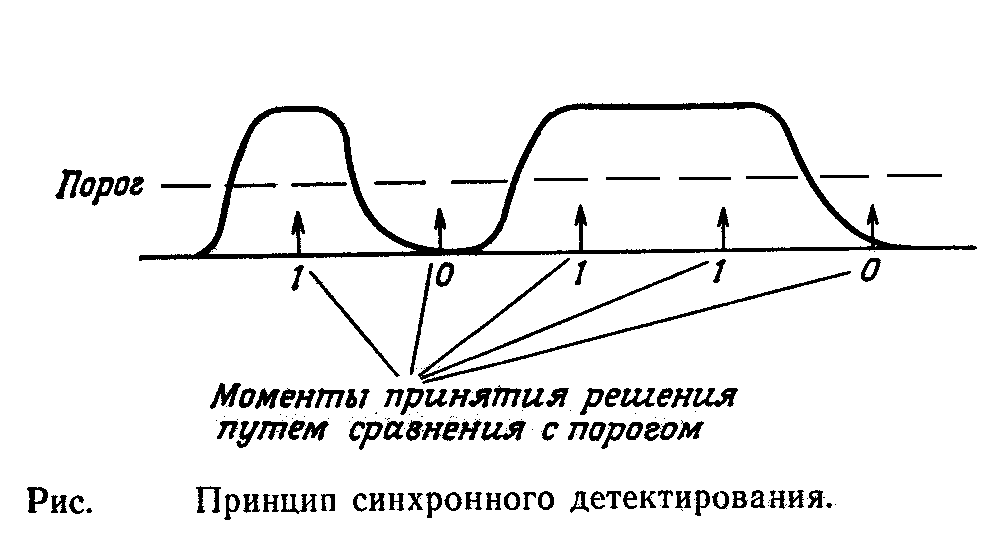
Рис.11. Принцип синхронного детектирования.

Описанная операция сравнения, кажущаяся с первого взгляда такой простой, на самом деле усложнена тем, что для правильного ее выполнения декодер должен правильно измерять уровень сигнала на входе. А сигнал на входе декодера содержит не только полезный сигнал, несущий информацию о передаваемых символах. Различного рода шумы, возникающие и в канале связи, и в процессе образования фотоэлектронов, тоже вносят свою "добавку" в мощность входного сигнала. Эти шумы могут иметь различный уровень, и при малых уровнях передаваемого сигнала они могут быть сравнимы с ним по всей мощности, сбивая тем самым с толку декодирующее устройство, пытающееся вынести решение о переданном символе.

Кроме того, сами импульсы света, распространяясь по оптическому волокну, претерпевают воздействие таких явлений, как дисперсия, затухание, рассеяние. Из-за этого наблюдаются хвосты импульса вне рабочего промежутка времени и наползание на соседние импульсы - так называемая межсимвольная помеха. Уровень оптической мощности, попадающей на приемное устройство, может оказаться даже разным для разных импульсов, а уровни сигнала, соответствующие символам "ноль", после влияния этих факторов могут уже не являться нулевыми.

Рис.12. Иллюстрация влияния дисперсии на импульсы света.

Все эти факторы, конечно же, не могут не влиять на правильность вынесения решения при декодировании. Поэтому ситуация, когда при передаче, например, символа "единица" декодер сформировал неправильный импульс "ноль", вполне возможна. Это могло произойти, например, вследствие сильного случайного ослабления сигнала в этот момент времени. Аналогично возможна и ситуация, когда при передаче нуля на выходе формируется единица. Из сказанного выше следует, что чем больше превосходство имеет мощность сигнала над мощностью шума, т.е. чем больше отношение "сигнал/шум", тем больше будет вероятность принятия правильного решения при восстановлении двоичных символов в декодере, и, следовательно, меньше будет значение вероятности ошибки. Для количественной оценки правильности формирования двоичных символов на выходе вводится величина "вероятность ошибки" - отношение числа ошибочно восстановленных символов к общему числу переданных символов за какой-либо промежуток времени (обычно это 1 с).

Чтобы при выполнении процедуры сравнения не учитывать тот вклад, который вносит мощность шума в сигнал, его необходимо исключить из входного сигнала, то есть выделить только ту его составляющую, которая образуется мощностью информационного сигнала.

Для анализа процесса работы декодера воспользуемся тем фактом, что напряжение входного сигнала в данный момент времени является случайной величиной с гауссовским законом распределения, средним значением u_m и дисперсией _u.

, где P_u(u) – вероятность того, что в данный момент времени напряжение входного сигнала равно u

Обозначим: u₁ - наиболее вероятный уровень сигнала при передаче символа «единица», наиболее вероятный уровень сигнала при передаче символа "ноль" положим равным нулю. Величину порога сравнения обозначим u_s.

Напомним, что при использовании кода NRZ, у которого длительность импульсов равна T, за этот интервал передается либо постоянный уровень для символа «единица» - и нулевой уровень для символа «ноль».

Тогда при передаче символа "единица" распределение входного сигнала будет иметь вид:

При передаче символа «ноль» вид распределения будет таким:

Изобразим эти функции на графике, задав также величину порога:

Рис.13. Распределение вероятности для оптического сигнала на входе нелегального фотодетектора.

Из графика видно, что при передаче символа «единица» декодер сформирует ошибочный символ «ноль» только тогда, когда значение входного напряжения будет лежать в пределах от - до u_s. Вероятность этого события будет равна:

Аналогично, при передаче символа «единица» будет сформирован ошибочный символ «ноль», если значение напряжения попадет в интервал от u_s до +. Вероятность этого события будет равна:

В системах передачи посылка символов «единица» и «ноль» априори считается равновероятной, поэтому для полной вероятности ошибки в этом случае можно применять соотношение:

И, если учесть, что вероятность ошибки для каждого символа будет одинаковой, то можно использовать следующее соотношение:

Из этого же предположения можно найти величину порога декодирования. Если приравнять

,то есть

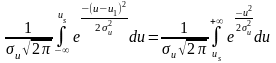
то, подставив в качестве переменной значение порога u_s, приравняем значения функций в точке порога.

На основании свойств монотонности функций имеем:

, откуда получаем значение порога:

Мы получили интуитивно ожидаемое значение, в котором порог равен половине амплитуды. Напомним, что это имеет место только в том случае, если посылка символов «ноль» и «единица» является равновероятной.

Вернемся теперь к выражению для вероятности ошибки. Полученное выше выражение можно упростить, используя замену переменной:

Тогда

Если теперь обозначить

то можно написать:

Полученная функция называется дополнительной функцией ошибок и используется очень часто. Ее протабулированные значения можно найти в математических справочниках.

Используя теперь полученное выше значение порога, можно выразить вероятность ошибки следующим образом:

Введем обозначение:

Тогда функция вероятности ошибки примет вид

Мы получили очень важный результат, который позволяет нам найти зависимость вероятности от интенсивности сигнала и шума. Ведь выражение для коэффициента Q, от которого зависит вероятность ошибки, содержит в числителе уровень сигнала, а в знаменателе - уровень шума, выражающийся дисперсией случайной величины напряжения. Следовательно, коэффициент Q пропорционален отношению "сигнал/шум", которое для цифровых систем связи обычно определяется как отношение максимального напряжения сигнала к действующему значению напряжения шума:

где Q- отношение "сигнал/шум"

Теперь полное выражение для зависимости вероятности ошибки от отношения "сигнал/шум" примет вид:

Теперь наша задача - выяснить, какие параметры фотоприемника влияют на отношение "сигнал/шум" и как его величина зависит от уровня принимаемой оптической мощности.

Основываясь на положениях теории цепей, для фотоприемного устройства можно нарисовать следующую эквивалентную схему:

Рис.14. Эквивалентная схема фотодетектора с предварительным усилителем.

Оптическая мощность, падающая непосредственно на фотоприемник, вызывает образование фототока. Фотоприемник имеет внутреннее сопротивление R_ф и емкость C_ф. Далее этот ток поступает на предусилитель. Он также имеет входное сопротивление R_a и емкость C_a. От сопротивления R_r и емкости C_r зависит коэффициент усиления данной схемы. Вклад дробового и теплового шумов учитывается введением в схему дополнительных источников тока i_q и i_t соответственно, а собственные шумы предусилителя отражены в источнике тока i_a и источнике напряжения e_a.

Очевидно, что элементы R_ф, C_ф, R_a и C_a можно заменить их эквивалентами:

Из теории цепей известно, что напряжение на выходе усилителя связано с входным током через коэффициент усиления, который примет вид:

Однако на практике величина 2ifR_rC_r оказывается очень малой, и при расчетах ею можно пренебречь. В результате выполняется соотношение:

Мы нашли выражение для величины сигнала. Расчет дисперсии случайной величины u, называемой также мощностью шума, выполняется аналогичным образом. Надо сказать, что анализу шумовых процессов на выходе фотоприемного устройства посвящен не один десяток работ, среди которых самыми примечательными являются работы Персоника, Гальярди и Карпа, Пратта, Форреста. Для доли, вносимой шумовыми токами, был получен результат:

или

,где N_iq, N_it, N_ia – спектральные плотности соответственно дробового, теплового и собственного шума усилителя

Для оценки доли, вносимой напряжением шума ², нужно рассчитать передаточную функцию усилителя между e_a и выходным напряжением при нулевом токе сигнала.

Такие расчеты проведены и получено выражение, часто используемое на практике:

,где N_ea – спектральная .плотность шума.

На основании предположения о независимости источников шума непосредственно получаем выражение для полной дисперсии шума:

где C=C_r+C_c

В соответствии с определением отношения сигнала к шуму, запишем:

Спектральные плотности для дробового и теплового шума также известны. На основании проведенных ранее исследований получены выражения:

• для дробового шума:

где q - заряд электрона ( q = 1,6 10^-19 Кл); i - фототок; M - коэффициент умножения фотодиода; x - дополнительная постоянная шума, зависит от типа полупроводника. для германия x1 для кремния x0,5

• для теплового шума

где k - постоянная Больцмана (k=1.3810^-23 Дж/К); T_k - абсолютная температура.

Эти выражения мы и будем использовать для расчетов.

Последнее, что необходимо уточнить - это значение фототока. Как известно, он связан с падающей на фотодиод мощностью света следующим соотношением:

где q - заряд электрона; h - постоянная Планка (h = 6,625 10^-34 Дж/с);  - частота излучения;  - коэффициент умножения фотодиода; P - падающая мощность; i_o - темновой ток фотодиода;

Теперь все готово, чтобы получить полное выражение для отношения "сигнал/шум", а также для вероятности ошибки:

,где

Подставив в это выражение все требуемые параметры, легко найти отношение "сигнал/шум", а затем и вероятность ошибки.