5.5 Неоднорідне рівняння теплопровідності з однорідними умовами

Розглянемо неоднорідне рівняння

, . (5.42)

з однорідними крайовими та початковою умовами

, (5.43)

. (5.44)

Шукаємо розв’язок цієї задачі у вигляді ряду Фур’є із застосуванням методу поділу змінних за власними функціями задачі (5.19)-(5.21) у вигляді, уважаючи параметром

, (5.45)

Для того, щоб знайти функцію , необхідно визначити функцію . Для цього запишемо у вигляді ряду

, (5.46)

де (5.47)

Обчислимо дві похідні за змінною та одну за змінною від функції (5.45) і підставимо їх та (5.46) до рівняння (5.42)

(5.48)

Це рівняння буде справджуватись, якщо вираз, що знаходиться у фіґурних дужках, буде дорівнювати нулю

= . (5.49)

Скориставшись умовою (5.43), отримаємо початкову умову для

. (5.50)

Розв’язавши задачу Коші для рівняння (5.49) з початковою умовою (5.50), отримаємо функцію у вигляді

. (5.51)

Підставивши (5.47) та (5.51) до (5.45), отримаємо розв’язок неоднорідного рівняння (5.42) з однорідними умовами (5.43) та (5.44) у вигляді

=

= , (5.52)

де = .

Або у вигляді , (5.53)

де – функція Гріна.

Ми розглянули неоднорідне рівняння з нульовими початковими умовами. Якщо початкова умова відмінна від нуля, то до розв’язку (5.52) необхідно додати розв’язок (5.37) або (5.39) однорідного рівняння з початковою умовою

+

Зауваження.

1. Для того, щоб ряд (5.35) був частинним розв’язком рівняння (5.19), він повинен бути збіжним і двічі диференційованим.

2. Хоча розв’язок (5.35) містить нескінчену суму, розв’язуючи конкретні фізичні задачі, можна обмежитись скінченним числом додатків.

5.6 Неоднорідне рівняння теплопровідності з неоднорідними умовами

Розглянемо неоднорідне рівняння

, (5.54)

з неоднорідними крайовими та початковою умовами

, (5.55)

(5.56)

Шукаємо розв’язок задачі (5.54)-(5.56) у вигляді суми двох функцій

, (5.57)

де – нова шукана функція, а – довільна функція, що задовольняє неоднорідним крайовим умовам.

Нехай , де – двічі диференційовані функції.

Підставляємо їх значення до крайових умов. Тоді маємо

,

.

Отже,

(5.58)

Функція повинна задовольняти неоднорідне рівняння

, (5.59)

де = -( )

та додаткові початкові й крайові умови

(5.60)

Після підстановки (5.58) у (5.60) умови стають однорідними, а задача (5.59)-(5.60) зводиться до задачі (5.42)-(5.44). Такий перехід від більш складних до більш простих задач називається редукцією задачі.

Приклад 5.3

У термічно тонкому циліндрі довжиною відсутні джерела тепла, початковий розподіл температури дорівнює . Кінці циліндра підтримуються при сталій температурі та . Визначити температуру циліндра у будь-якій точці та у будь-який момент часу.

Розв’язок. Маємо першу крайову задачу для одномірного однорідного рівняння теплопровідності з неоднорідними граничними умовами

, (5.61)

, (5.62)

(5.63)

Оскільки граничні умови не залежать від часу, джерела тепла відсутні, то розв’язок рівняння (5.61 ) шукаємо у вигляді суми функцій

(5.64)

Для функції маємо крайову задачу для звичайного диференціального рівняння другого порядку

, (5.65)

а для функції - однорідну крайову задачу для однорідного рівняння теплопровідності

, , (5.66)

, (5.67)

. (5.68)

Розв’язок задач1 (5.65) можна записати у вигляді = . Урахувавши крайові умови маємо

= (5.69)

Підставивши (5.69) до (5.67), отримаємо початкову умову для задачі (5.66)-(5.68). Це задача тотожна задачі (5.16)-(5.18). Її розв’язок має вигляд (5.37), (5.39).

Задача 5.4

Температура тонкої теплопровідної нитки нескінченної довжини у початковий момент часу була розподілена за законом . Визначити температуру нитки у будь-який момент часу у будь-якій його точці, уважаючи, що коефіцієнт температуропровідності .

Розв’язок.

Маємо задачу Коші для одномірного рівняння теплопровідності

, (5.70)

. (5.71)

З фізичної точки зору ця задача схожа на задачу (5.16)-(5.18), але відсутні граничні умови. Скориставшись методом поділу змінних, розв’язок рівняння (5.70) можна записати у вигляді

(5.72)

Він задовольняє рівняння (5.70), але при цьому залишаються невідомими власні числа коли ,. Їм відповідали коефіцієнти та , які знаходили із крайових умов. Чим довша нитка, тим коротша відстань між власними числами та ( коли ). Отже кожному власному значенню відповідає частинний розв’язок

. (5.73)

Загальний розв’язок знаходимо не шляхом підсумовування (5.33), а шляхом інтеґрування виразу (5.73)

. (5.74)

Ми отримали розв’язок, що задовольняє рівняння (5.70), але він повинен ще й задовольняти початкову умову (5.71)

. (5.75)

Звідси зрозуміло, що якщо функція абсолютно інтеґрована для , то задача звелась до розкладу цієї функції у інтеграл Фур’є. Тому можемо записати

, (5.76)

де

(5.77)

Підставляючи (5.77) до (5.74) та зваживши на те, що , отримаємо розв’язок задачі у вигляді

. (5.78)

Інший розв’язок можна отримати після підстановки (5.77) до (5.78) виконання перетворень і зміни порядку інтеґрування

. (5.79)

Після заміни можна внутрішній інтеграл у (5.79) записати у вигляді, відомому з математичного аналізу

. (5.80)

Провівши зворотну заміну , отримаємо розв’язок задачі у вигляді

. (5.81)

Щоб зрозуміти фізичний зміст отриманого розв’язку, допустимо, що у початковий момент часу температура нескінченної нитки дорівнювала нулю всюди, окрім околу точки , де (рис. 5.1). Нехай у момент у елементі нитки завдовжки виділяло тепло у кількості , яке привело до збільшення на цьому відрізку температури до . Тоді формула (5.81) набуває вигляду

. (5.82)

Перейшовши до границі та спрямувавши , будемо вважати, що у точці миттєво виділилося тепло у кількості . При цьому температурний розподіл у нитці має вигляд

(5.83)

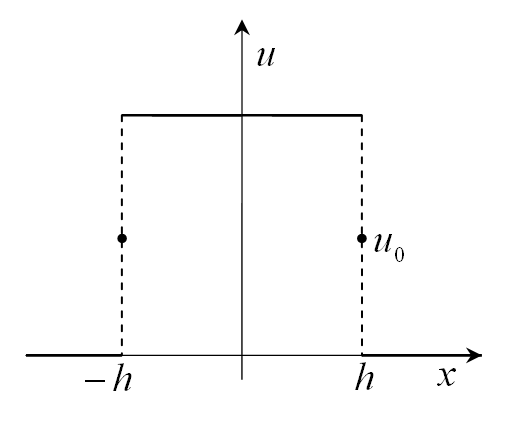
Рисунок 5.1

Скориставшись властивістю – функції Дірака, можемо записати, що

(5.84)

Якщо , а , то температура нитки обчислюється за формулою

, (5.85)

а функція називається функцією Гріна.

Графік температурного розподілу (5.85) зображено на рисунку 5.2.

Рисунок 5.2

Як відомо, загальна кількість тепла, що виділяється у нитці за час , визначається за формулою

,

але відомий як інтеґрал Пуассона. Тому маємо , що узгоджується із законом збереження енергії.