5 Рівняння параболічного типу

5.1 Основні поняття

Найбільш характерними представниками рівнянь параболічного типу є рівняння теплопровідності та дифузії. Розглянемо перше із них.

Розглянемо|розгледимо| довільний об’єм| , обмежений поверхнею деякого теплопровідного тіла, у кожній точці якого задана температура , що залежить від координат та часу. Якщо в області температура , то в ньому відбувається перерозподіл тепла. Розповсюдження тепла відбувається від більш теплих точок середовища до більш холодних. Основним законом поширення тепла у просторі є перший закон теплопровідності Фур'є.

Перший закон теплопровідності Фур'є. Кількість тепла (потік) , що проходить через одиницю|поодинокий| площі за одиницю часу, пропорційна до нормальної похідної від температури

. (5.1)

Знак “мінус” означає, що тепло поширюється у напрямі, протилежному до нормалі, а нормаль, як відомо, указує напрям зростання функції, у даному випадку температури .

Нехай в області діють джерела тепла об’ємною щільністю Тоді кількість тепла , що виділяється цими джерелами в об’ємі | за проміжок часу визначається за формулою або у вигляді інтеґрала

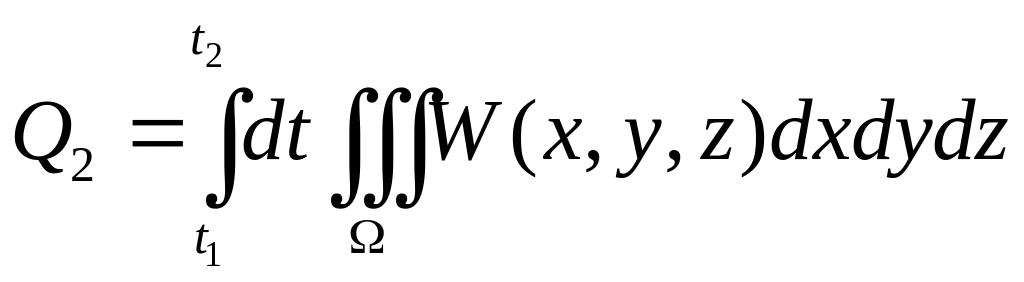. (5.2)

Згідно із законом збереження|зберігання| енергії це тепло частково накопичується в об’ємі за рахунок його теплоємності, а частково втрачається|розгублюється| через поверхню за рахунок теплообміну з навколишнім середовищем.

Накопичення об’ємної енергії |можна записати у вигляді

|виді| ,

де – відповідно теплоємність і щільність середовища, що розігрівається, або у інтеґральній формі

(5.3)

де – диференціал об’єму.

Втрату тепла через поверхню , що обмежує об’єм можна записати у вигляді

(5.4)

де – щільність потоку тепла через поверхню або

(5.5)

де – одиничний|поодинокий| орт зовнішньої до нормалі.

Скориставшись формулою Гауса - Остроградського

рівність (5.4) можна записати у вигляді

.

Баланс тепла області означає, що кількість тепла накопиченого у об’ємі дорівнює сумі тепла, виділеного джерелами та втраченого через поверхню у навколишнє середовище

,

або у інтеґральній формі в прямокутній системі координат

. (5.6)

У зв’язку з тим, що об’єм і проміжок часу довільні, інтеґральна рівність (5.6) можлива тоді й тільки|лише| тоді коли вираз, що знаходиться|вираження| під знаком інтеграла у (5.6), дорівнює нулю

(5.7)

У загальному|спільному| випадку, коли характеристики та залежать від температури та її ґрадієнта співвідношення, (5.7) є квазілінійним диференціальним рівнянням з частинними похідними параболічного типу. Перетворимо (5.7), враховуючи, що

.

У такому випадку рівняння (5.7) набуває вигляду|виді|

, (5.8)

або у прямокутній системі координат

,

де – коефіцієнт теплопровідності.

Далі, якщо не залежить від , а , то рівняння (5.8) запишемо у вигляді|вид|

(5.9)

Якщо у тілі є|наявний| стоки або джерела тепла, але|та| температура не залежить від часу, тобто , то рівняння (5.9) можна записати у вигляді

(5.10)

Це рівняння називається рівнянням Пуассона.

Нарешті,|урешті| якщо і джерела відсутні, то одержуємо|отримуємо| рівняння Лапласа

. (5.11)

Одержані|отримані| лінійні та нелінійні рівняння описують температурне поле області залежно від часу та просторових змінних.

Основною задачею|задачею| теорії теплопровідності є знаходження|з'являється,являється| розв’язків рівнянь (5.8)-(5.11), що задовольняє певним початковим й крайовим|крайовій| умовам. Ці розв’язки описують температурні поля в області, розігрівається або охолоджується.