3.4. Представление чисел в компьютере

Целые числа могут представляться в компьютере без знака или со знаком.

Целые числа без знака обычно занимают в памяти компьютера 1 или 2 байт и принимают в однобайтовом формате значения от 00000000₂ до 11111111₂, а в двухбайтовом формате – от 00000000 00000000₂ до 11111111 11111111₂ .

Целые числа со знаком обычно занимают в памяти компьютера 1, 2 или 4 байт, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «+» кодируется нулем «0», а знак «–» – единицей «1».

В компьютерной технике применяются три формы кодирования целых чисел со знаком:

– прямой код;

– обратный код;

– дополнительный код.

Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде.

Число 1₁₀ = 1₂ : Число 127₁₀ = 1111111₂:

0 0 0 0 0 0 0 1 0 1 1 1 1 1 1 1

Знак числа «–» Знак числа «–»

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

Прямой код числа –1: Прямой код числа –127:

_{1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1}

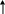Знак числа «–» Знак числа «+»

Прямой код: в знаковый разряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины.

Обратный код получается инвертированием всех цифр двоичного кода, абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями.

Примеры.

Число: –1. Число: –127

Код модуля числа: 00000001 Код модуля числа: 01111111

Обратный код числа: 11111110 Обратный код числа : 10000000

Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.

Дополнительный код числа –1: Дополнительный код числа –127:

Используя прямой, обратный и дополнительный коды, можно свести операцию умножения к последовательности сложений и сдвигов, а операцию деления – к многократному прибавлению к делителю дополнительного кода делителя.

Отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа [31].

3.5. Вещественные числа

Вещественные числа (конечные и бесконечные десятичные дроби) хранятся и обрабатываются в компьютере в формате с плавающей запятой.

Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так, число А может быть представлено в виде

A = m qⁿ,

где т – мантисса числа; q – основание системы счисления; п – порядок числа.

Для однозначности представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию

1/n = m < 1.

Это означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.

Пример. Преобразуем числа в экспоненциальную форму с нормализованной мантиссой:

421,637 = 0,421637  10³; 0,000286 = 0,286  10^4.

Число в форме с плавающей запятой занимает в памяти компьютера 4 или 8 (зависит от точности) байт. При записи числа с плавающей запятой выделяют разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Арифметические операции. При сложении и вычитании чисел в формате с плавающей запятой сначала производится подготовительная операция выравнивания порядков. Порядок меньшего (по модулю) числа увеличивается до величины порядка большего (по модулю) числа. Для того чтобы величина числа не изменилась, мантисса уменьшается в такое же число раз (сдвигается в ячейке памяти вправо на число разрядов, равное разности порядков чисел).

После выполнения операции выравнивания одинаковые разряды чисел оказываются расположенными в одних и тех же разрядах ячеек памяти. Теперь операции сложения и вычитания чисел сводятся к сложению или вычитанию мантисс.

После выполнения арифметической операции для приведения полученного числа к стандартному формату с плавающей запятой производится нормализация, т.е. мантисса сдвигается влево или вправо так, чтобы ее первая значащая цифра попала в первый разряд после запятой [14].

Пример. Произвести сложение чисел 0,1  2³ и 0,1  2⁵ в формате с плавающей запятой.

Произведем выравнивание порядков и сложение мантисс:

При умножении чисел в формате с плавающей запятой порядки складываются, а мантиссы перемножаются. При делении из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя.

Пример. Произвести умножение чисел 0,1  2³ и 0,1  2⁵ в формате с плавающей запятой. После умножения будет получено число 0,01  2⁸, которое после нормализации примет вид 0,1  2⁷.

Лекция 4

Логические основы компьютера