Опис алгоритмів обчислення інтерполяційного поліному Ньютона в заданих точках Перший алгоритм

Обчислення інтерполяційного полінома Ньютона доцільно організувати у вигляді функції що повертає значення y інтерполяційного полінома Ньютона в точці x. По заданих масивах X,Y розмірності n необхідно обчислити значення y інтерполяційного полінома Ньютона в точці x. Необхідно переконатися у відсутності співпадаючих значень у масиві аргументів функції Х, як і в методі Лагранжа. Звичайно необхідно обчислити значення інтерполяційного полінома в декількох точках, а ці дії варто виконувати тільки один раз. Якщо серед точок x_i (i =1, n) немає співпадаючих, то необхідно обчислити суму – значення інтерполяційного полінома P(x) в заданій точці x.

Для цього послідовно обчислюємо скінчені різниці P(x₁, x₂), P(x₁, x₂, x₃) і т.д. Вони будуть зберігатися в масиві R. У блоці 1 масиву R привласнюється масив Y, в мові Паскаль для однотипових масивів таке присвоєння можливе! При програмуванні на інших мовах це присвоєння треба виконувати у циклі: for i=1 to n do R[i]=Y[i].

Значення інтерполяційного полінома в точці x₀ являє собою суму добутків виду:

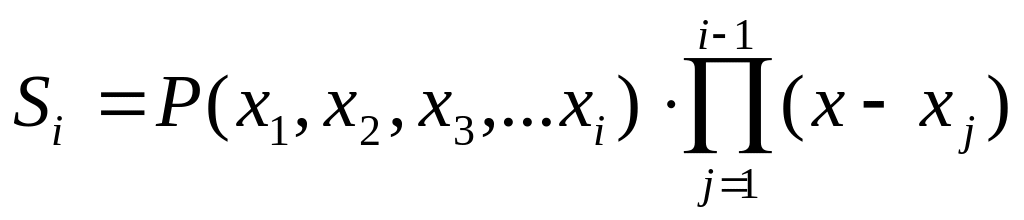
Сума S_i накопичується в змінній y0, добуток у змінній p (блок 6). Крім того, необхідно обчислювати чергову розділену різницю. Для цього служать блоки циклу 4 і 5.

Потрібно звернути увагу, що в блоці 6 весь час вираз множиться на R[1]. Однак у R[1] спочатку зберігається значення P(x₁), потім P(x₁, x₂), P(x₁, x₂, x₃) і т.д.