Тестілік тапсырмалар

$$$1

Кездейсоқ шаманы тұрақты санға көбейтсе, оның дисперсиясы:

А) сол санға көбейтіледі;

В) сол санның квадратына көбейтіледі;

C) сол санның ½ -не көбейтіледі;

D) сол санның ¼ -не көбейтіледі;

Е) (-1)-ге көбейтіледі.

$$$ 2

Кездейсоқ шаманың дисперсиясы:

А) кездейсоқ шама мен оның математикалық үмітінің айырымының квадратына тең;

В) кездейсоқ шама мен оның математикалық үмітінің айырымының математикалық үмітіне тең;

C) кездейсоқ шама мен оның математикалық үмітінің айырымының квадратының математикалық үмітіне тең;

D) ауытқудың квадратының математикалық үмітіне тең;

Е) кездейсоқ шама мен оның математикалық үмітінің айырымының кубының математикалық үмітіне тең.

$$$ 3

Стандартты қалыпты үлестірудің параметрлерін көрсет

А)

В)

C)

D)

Е)

$$$ 4

Тығыздығы үздіксіз кездейсоқ шама қалай үлестірілген

A) қалыпты үлестірілген;

B) көрсеткішті үлестірілген;

C) бірқалыпты үлестірілген;

D) Стьюдент үлестіруімен;

E) Вейбулл үлестіруімен.

$$$ 5

Егер бағаның математикалық үміті бас жиынның сәйкес сипаттамасына тең болса, онда баға

A) тиімді;

B) жылжымаған;

C) орнықты;

D) жылжыған;

E) стандартты.

$$$ 6

Егер эконометриялық моделде тек қана бір түсіндіруші айнымалы болса, онда ол былай аталады

A) қос сызықтық регрессия;

B) қос регрессия;

C) қос сызықтық емес регрессия;

D) жиындық сызықтық регрессия;

E) жиындық регрессия.

$$$ 7

Дискретті кездейсоқ шама - тің математикалық үміті қай формуламен есептеледі?

A) ;

B) ;

C)

D)

E) .

$$$ 8

- кездейсоқ шаманың үлестіру кестесі берілген

	1	2	3	4
	0.3	0.1	0.2	0.4

Табу керек:

A) 15;

B) 10.8;

C) 43.2;

D) 13.8;

E) 2.8.

$$$ 9

- кездейсоқ шаманың үлестіру кестесі берілген

X	1	3	5	7	9
P	b	2b	3b	4b	5b

b –параметрін анықтаңыз

A) 1/15;

B) 4/15;

C) 2.1;

D) 0.15;

E) 3.

$$$ 10

Үздіксіз кездейсоқ шама үлестіру функциясымен берілген

Кездейсоқ шама - тің [1;3) аралығында мән қабылдау ықтималдығын есептеңіз.

A) 0.25;

B) 0;

C) 3/5;

D) 8/25;

E) 1/25.

$$$ 11

X және y шамаларының арасындағы байланыс неғұрлым тығыз болса, соғұрлым детерминация коэффициенті қандай санға жақын болады

A) 1;

B) 0;

C) -1;

D) ;

E) 2.

$$$ 12

Үлестіру функциясы бойынша берілген кездейсоқ шама X-тің интервалында мән қабылдау ықтималдығы тең

A) ;

B) ;

C) ;

D) ;

E) .

$$$ 13

Елде соңғы 10 жыл ішінде жылдық инфляция қарқынының (%) статистикасы келтірілген: 2.8; 3.2; 5.1; 1.8; -0.6; 0.7; 2.1; 2.7; 4.1; 3.5. Инфляцияның орта қарқынының жылжымаған бағасын табыңыз.

A) 2.54;

B) 4.64;

C) 8;

D) 3.5;

E) 6.4.

$$$ 14

және үйлесімсіз кездейсоқ шамалар болса, . табыңыз.

A) 24;

B) 0;

C) 21;

D) -5;

E) 44.

$$$ 15

және үйлесімсіз кездейсоқ шамалар болса, . неге тең?

A) 12;

B) 23;

C) 10;

D) 61;

E) 66.

$$$ 16

Бас жиыннан көлемі таңдама алынған

	1	3	6	26
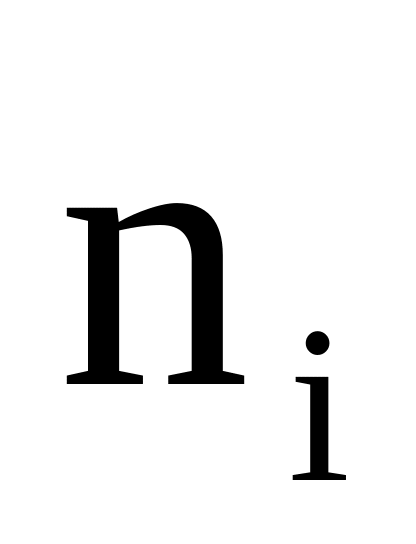
	8	40	10	2

Бас жиынның орташасының жылжымаған бағасын табыңыз

A) 2;

B) 34;

C) 4;

D)19;

E) 1.

$$$ 17

Көлемі таңдама бойынша бас жиынның дисперсиясының жылжыған бағасы табылған. Бас жиынның дисперсиясының жылжымаған бағасын табыңыз.

A) 24;

B) 3.075;

C) 3.75;

D)25.0;

E) 2.75.

$$$ 18

Құрылған моделдің сапасын қай көрсеткіш анықтайды?

A) математикалық үміт;

B) регрессия коэффициенті;

C) ковариация коэффициенті;

D) детерминация коэффициенті;

E) орташа квадраттық ауытқу.

$$$ 19

Кездейсоқ шама үлестіру тығыздығымен берілген. Параметр -ны анықтаңыз.

A) 12;

B) 3;

C) 2.4;

D) -1;

E) 10.

$$$ 20

Күнделікті сатылатын тауар көлемін талдау үшін 20 күн ішіндегі мәліметтер алынған: 5, 6, 2, 3, 7, 7, 6, 6, 10, 11, 6,10, 11, 6, 4, 5, 6, 4, 5, 6. Таңдаманың ортасын есепте.

A) 6.25;

B) 5.2;

C) 3.5;

D) 8.25;

E) 6.3.

$$$ 21

Бас жиынның үлестіру параметрлерінің шамалары туралы жорамал қалай аталады?

A) статистикалық болжам;

B) математикалық үміт;

C) орташа квадраттық ауытқу;

D) гетероскедастық;

E) автокорреляция.

$$$ 22

, болса таңдаманың ковариация коэффициенті қандай мән қабылдайды?

A)

B)

C)

D)

E)

$$$ 23

Тұрғындардың тұтыну шығыны ( ) және колда бар кірісі ( ) арасындағы тәуелдік: түрінде берілген. Регрессия теңдеуі бойынша дұрыс тұжырымды көрсетіңіз: (көрсеткіштер млн. теңгемен берілген):

A) қолда бар кіріс мөлшері 1 млн. теңге артуы тұтыну шығынының 100 мың теңге өсуіне әкеледі;

B) қолда бар кіріс мөлшері 1 млн. теңге артуы тұтыну шығынына әсер етпейді;

C) кіріс мүлдем жоқ болса, тұтыну шығыны 100 мың теңгені құрайды;

D) қолда бар кіріс мөлшері 1 млн. тенге артуы тұтыну шығынының 250 мың теңге өсуіне әкеледі;

E) қолда бар кіріс мөлшері 1 млн. тенге кемуі тұрғындардың тұтыну шығынына әсер етпейді.

$$$ 24

X және Y кездейсоқ шамалары келесі кестемен берілген

X \Y	-2	2
2	0	0.5
4	0.25	0.25

X және Y шамаларының математикалық үміттерін анықтаңыз.

A) М(Х) = 0; М(Y) = 1;

B) М(Х) = 1; М(Y) = 1;

C) М(Х) = 0; М(Y) = 0;

D) М(Х) = 3; М(Y) = 0;

E) М(Х) = 3; М(Y) = 1.

$$$ 25

Таңдаманың корреляция коэффициенті қай формуламен анықталады

A)

B)

C)

D) ;

E)

$$$ 26

Регрессия теңдеуінде екі немесе бірнеше түсіндіруші айнымалылар арасындағы тығыз корреляциялық байланыс қалай аталады

A) гомоскедастық;

B) гетероскедастық;

C) мультиколлинеарлық;

D) бірінші текті автокорреляция;

E) автоколлинеарлық

$$$ 27

Қос сызықтық регрессия параметрі ең кіші квадраттар әдісі бойынша келесі формуламен анықталады

A)

B)

C)

D)

E)

$$$ 28

Дұрыс тұжырымды таңдаңыз:

A) детерминация коэффициенті [-1; 1) аралығында мән қабылдайды;

B) егер регрессия коэффициентінің стандартты қатесі оның модулінен үлкен болса, онда регрессиялық талдау бойынша табылған баға жақсы деп саналады;

C) детерминация коэффициентінің статистикалық маңыздылығын тексеру үшін Стьюденттің - статистикасы қолданылады;

D) ең кіші квадраттар әдісін пайдаланғанда кездейсоқ шамаларына Гаусс- Марков шарттары қойылмайды;

E) қос сызықтық регрессиялық талдауда теориялық корреляция коэффициенті нөлге теңдігі туралы - критерий және болжамы туралы - критерий бір-біріне эквивалент.

$$$ 29