4.5 Регрессия теңдеуінің жалпы сапасын тексеру. Детерминация коэффициенті

Регрессияның әрбір коэффициентінің маңыздылығын тексергеннен кейін әдетте оның регрессия теңдеуінің жалпы сапасы тексеріледі. Егер барлық нүктелер құрылған теңдеудің бойында жататын болса, онда -тің -ке тәуелділігі -тің мәндерінен байқалады. Регрессия теңдеуінің жалпы сапасының қосындылық өлшемі - детерминация коэффициенті.

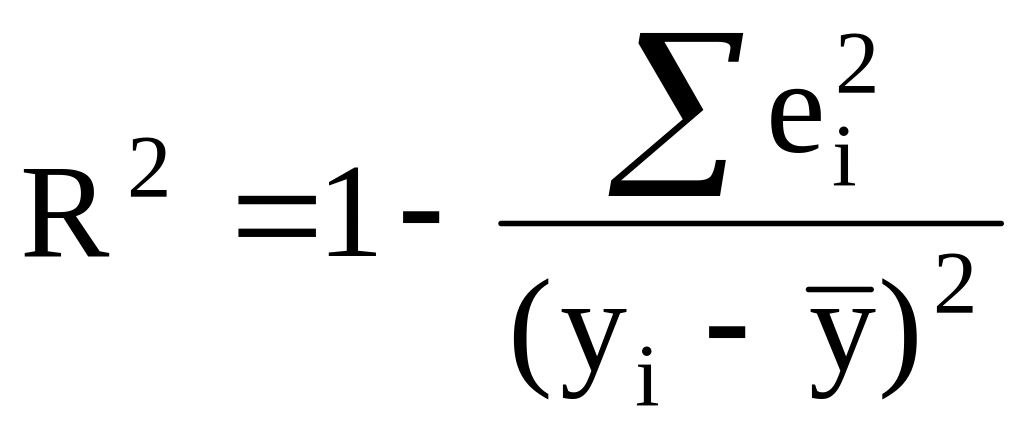(27)

Коэффициенттің мағынасын түсіндірейік. Регрессияның эмпирикалық теңдеуі:

. (28)

Бақыланған нақты мәндері ; модель бойынша мәндері , ауытқуы шамасы

. (29)

Бұл өрнекті

(30)

немесе

,

-бақыланатын -ші нүктенің тәуелді айнымалының орташасы -тен ауытқуы; - регрессия түзуіндегі осы нүктенің -дан ауытқуы; -осы нүктенің модель бойынша регрессия теңлеуімен анықталған мәнінен ауытқуы. Барлық ауытқулар тәуелді айнымалының өсі бойынша есептеледі.

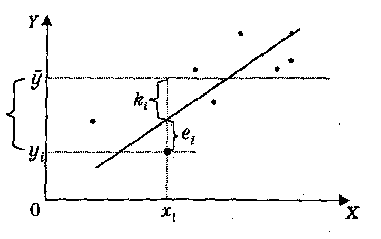
Сурет 8

(31)

, онда келесі қатынас орындалады

(32)

соңғы теңдеу жалпы квадраттар қосындысы, яғни -тің қарағанда бытырап орналасуының өлшемі деп қарастыруға болады.

түсіндіруші квадраттар қосындысы.

қалдық квадраттар қосындысы.

(32) теңдігін сол жағындағы қосындыға бөліп,

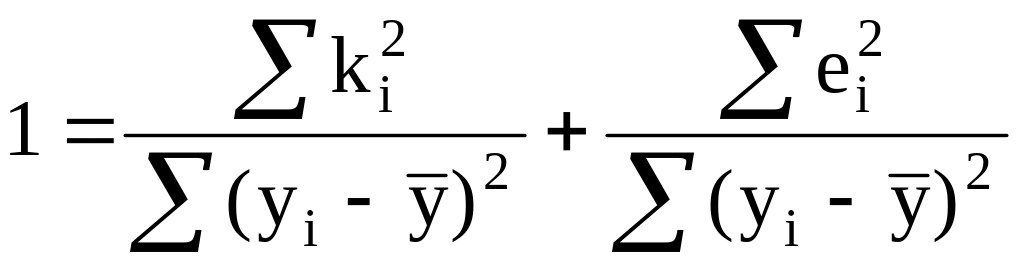(33)

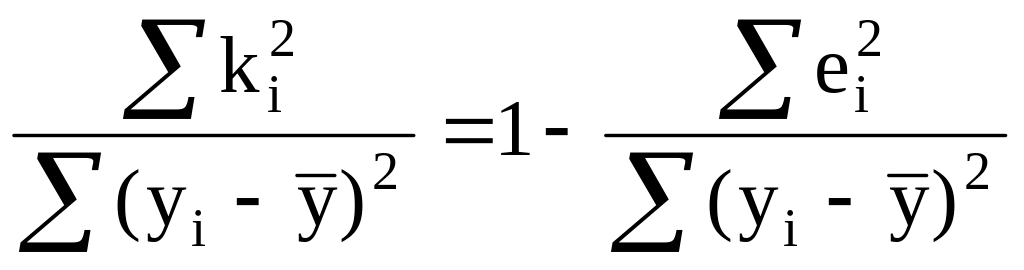
Белгілеу енгізетін болсақ

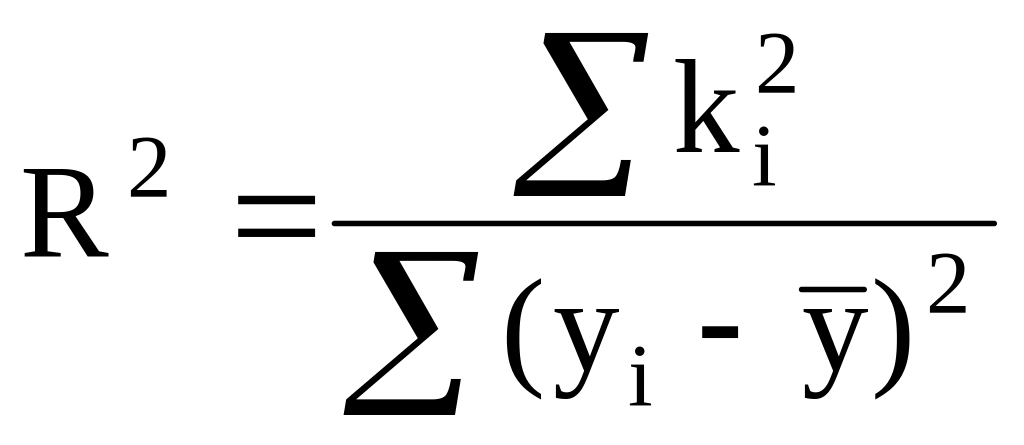, ендеше (34)

4.6 Түсіндіруші айнымалыларды таңдау

Регрессия теңдеуіне кіргізетін факторлар құрамын анықтау үшін алдымен олардың өзара байланыстарының теориялық көріністерін қолданады. Бейнеленген факторлар сандық өлшемді болу керек. Түсіндіруші айнымалылар құрамына тұтынушылар талғамының өзгеруін кіргізу қиын. Айнымалылардың спецификасы қате болу себептері:

а) теңдеуге қажетті түсіндіруші айнымалы кіргізілмеу;

b) теңдеуге қажетсіз түсіндіруші айнымалы кіргізу.

(35)

теңдеуіне айнымалыны кіргізбегенде

(36)

теңдеуі талданады. Онда (36) теңдеу үшін айнымалының коэффициенті мына формуламен есептеледі

Егер айнымалылары корреляциялық байланыста болса, онда нақты (35) теңдеуімен анықталатын болғандықтан математикалық үміт:

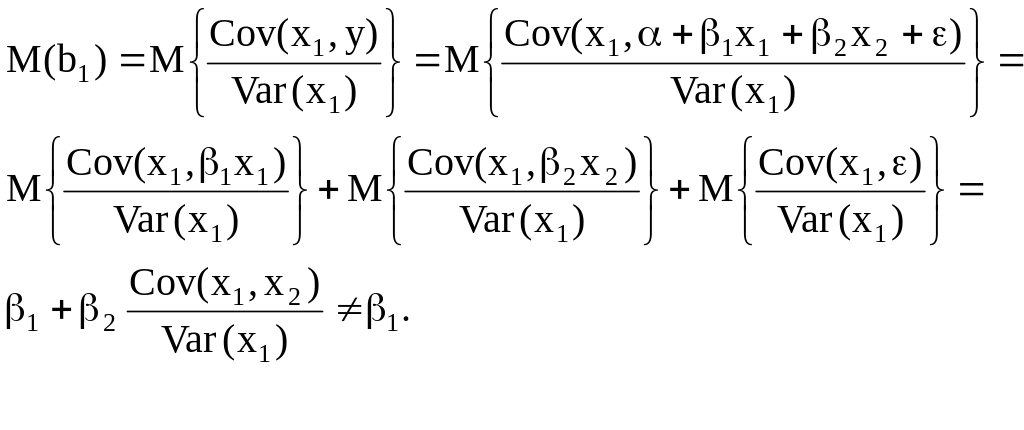
Теңдеуге қажет айнымалыны енгізбеу оның коэффициенттерінің бағасының жылжыған болуына әкеліп соқтырады. Бұл жағдайда бағалар жылжымаған, бірақ тиімсіз болады. және айнымалылар арасында корреляциялық байланыс неғұрлым жоғары болса, соғұрлым коэффициентінің шамасы жоғары болады. Регрессия теңдеуіне артық түсіндіруші айнымалыны кіргізу регрессия теңдеуінің сапасын жақсарта алмауымен қатар коэффициенттерінің статистика бойынша маңызды емес болуына келтіруі мүмкін.