3.3. Образы и прообразы

В общем случае при отображении f : ХY элемент из У может быть образом не одного, а нескольких моментов множества X. Совокупность всех элементов, образом которых является данный элемент у из У, назы­вается полным прообразом элемента у и обозначается f^--1(у).

Пусть Q — некоторое подмножество множества X, на котором определено отображение f. Совокупность элементов f(q), являющихся образами всех элементов множества Q, называется образом множества Q и обозначается f(Q). В свою очередь, для каждого множества К из У определяется его полный прообраз f^--1(K) как совокупность всех тех элементов из X, образы которых принадлежат К.

Основные свойства отображении выражаются соотношениями:

Образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов. Но можно показать, что

3.4. Подстановки как отображения

Взаимно-однозначное ото­бражение множества N = (1, 2, ..., n) на себя называется под­становкой п чисел (или подстановкой п-й степени). Обычно при­нято записывать подстановку двумя строками, заключенными в скобки. Первая строка содержит аргументы (первые координаты) подстановки, а вторая — соответствующие им образы (вторые коор­динаты). Например, взаимно-однозначное соответствие четырех чисел, заданное множеством упорядоченных пар {(1, 2), (2, 4), (3, 3), (4, 1)} запишется как подстановка а четвертой степени

в которой 1 переходит в 2, 2 – в 4, 3 - в3 и 4 - в 1.

Так как безразлично, в каком порядке следуют упорядоченные пары отображения, то одна и та же подстановка допускает различ­ные представления:

Каждая строка в записи подстановки п-й степени содержит п различных чисел, расположенных в определенном порядке, т. е. представляет собой некоторую перестановку п чисел 1, 2, ..., п. Если обозначить i-е элементы перестановок через и , причем то подстановку п-й степени можно представить как

Поскольку число всех перестановок из п чисел равно п!, то число всех различных перестановок п-й степени, как и число всевозможных способов записи любой из таких подстановок, также равно п!

Тождественная подстановка п-й степени e_п переводит каждое число в себя. Очевидно, одной из записей e_п является следующая:

Если в подстановке а поменяем местами ее перестановки, то получим подстановку а^-1, симметричную а. Например:

Композицией подстановок п-й степени а и b называется подста­новка п-й степени с=ab, являющаяся результатом последователь­ного выполнения сначала а, затем b. Например:

т.к. 1 переходит в 2, а 2 –в 4, т.e. в результате 1 переходит в 4 и т.д.

Очевидно, если а - подста­новка п-й степени, то:

два числа в перестановке образуют инверсию, когда меньшее из них расположено правее большего. Подстановка называется четной, если общее число инверсий в ее строках (перестановках) четно, и нечетной - в противном слу­чае. Каждой пере­становке можно сопоставить число инверсий в ней, которое подсчи­тывается следующим образом: для каждого из чисел определяется количество стоящих правее его меньших чисел, и полученные результаты складываются. Например, подстановка

нечетная, т.к. число инверсий в верхней перестановке 3+1+2+0+0+0=6 и в нижней перестановке 4+2+0+1+0+0=7, т.е. общее число инверсий 6+7=13.

Всякую подстановку можно разложить в произведение циклов, множества элементов кото­рых попарно не пересекаются. Цикл - это такая подстановка

=

которая переводит в , в , ..., в и в , а остальные элементы переходят в самих себя. Сокра­щенная запись цикла сводится к перечислению мно­жества элементов, которые циклически переходят друг в друга, а количество этих элементов k определяет длину (порядок) цикла. Так,

= (1, 4, 5)(2, 3)(6)

Цикл длины 1 представляет собой тождественную подстановку и часто не записывается. Подстановка, все п элементов которой образуют цикл, называется круговой или циклической. Цикл длины 2 называют транспозицией (это подстановка, переставляющая только два элемента). Всякая подстановка представляется произведением транспозиций, например:

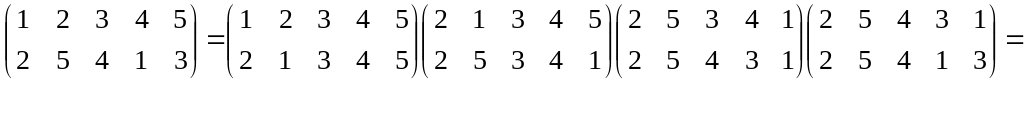
Заметим, что подобное разложение может содержать циклы с общими элементами и при этом оно не является единственным. В то же время разложение подстановки на независимые циклы (без общих элементов) всегда можно осуществить только единственным способом.

Наглядное представление о подстановках дают их графы, построенные на множестве п вершин, соответствующих числам 1,2, .... п. На рис. 3.2а пока­заны графы подстановок а (сплошными линиями) и b (штриховыми) и на рис. 3.2б - граф их композиции с=ab:

а)

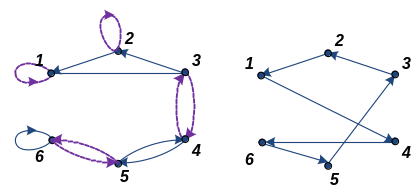
б)

Рис. 3.2. Графы подстановок (а) и композиции подстановок (б)

Циклам подстановок соответствуют простые циклы графа (циклы длины 1 изображаются петлями), причем граф состоит исключи­тельно из таких циклов. Композиция подстановок на рис. 3.2б содержит только один цикл, которому соответствует единственный цикл графа, т. е. является циклической.