4. Сечения

Рассмотрим отношение R  Х  У; если , то сечение по , отношения R, обозначаемое , есть множество таких, что . Множество всех сечений отношения R называют фактор-множеством множества У по отношению R и обозначают . Оно полностью определяет отношение R.

Пример. Пусть:

Тогда

Если записать под каждым элементом из Х соответствующее сечение отношения R, то элементы второй строки образуют фактор-множество :

5. Симметризация отношения

так как отношения - это мно­жества, то над ними можно выполнять все теоретико-множествен­ные операции. Кроме того, определяются специфические для отно­шения операции: обращение (симметризация) и композиция.

Отношение, симметричное (обратное) некоторому отношению , обозначается через и представляет собой подмно­жество множества Y  X, образованное теми парами для которых . Переход от R к осуществляется взаим­ной перестановкой координат каждой упорядоченной пары. Так, обратное отношение для «х делится на у» будет «у есть делитель х» и для приведенного в (2.1) примера выражается множеством .

При переходе от R к область определения становится об­ластью значений, и наоборот. Матрица обратного отношения полу­чается транспонированием исходной матрицы. Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.

2.6 Композиция отношений

Пусть даны три множества X, Y, Z и два отношения и . Композиция отноше­ний А и В есть отношение С=АВ, состоящее из всех тех пар , для которых существует такое уY, что (х, у)  А и (у, z)  В.

Сечение отношения С=АВ по х совпадает с сечением отношения В по подмножеству А(х) Y, т. е. С(х) = В (А(х)).

Граф композиции отношений получается из графов исходных отношений заменой двух стрелок, конец одной из которых является началом другой, на стрелку, начало которой совпадает с началом первой, а конец с концом второй.

Матрица композиции отношений является произведением матриц исходных отношений, взятых в обратном порядке, с заменой всех ненулевых элементов на 1.

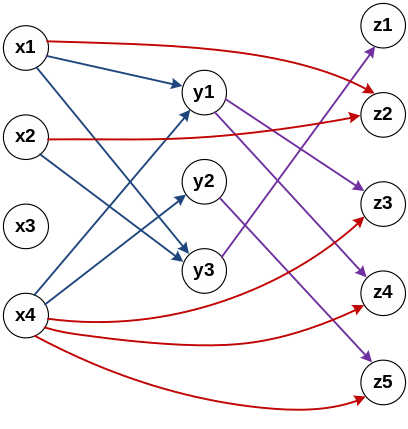
Пример. Пусть ;

Тогда

Граф композиции этих отношений приведен на рис. 2.3.

Рис. 2.3. Граф композиции С=АВ

;

2.7. Свойства бинарных отношений

Пусть R – бинарное отношение в множестве Х.

1) R называется рефлексивным, если всякий элемент связан этим отношением сам с собой

(ЕR)

2) R называется антирефлексивным, если никакой элемент не связан этим отношением сам с собой

(ЕR=)

Граф рефлексивного отношения в каждой вершине содержит петлю, граф антирефлексивного отношения петель не имеет.

Матрица рефлексивного отношения имеет на главной диагонали все 1, матрица антирефлексивного отношения – нули.

3) R называется симметричным, если x связан отношением R с y тогда и только тогда, когда y связан отношением R с x. пара тогда и только тогда, когда ему принадлежит пара .

( )

Матрица симметричного отношения является симметричной относительно главной диагонали. В графе симметричного отношения наличие стрелки из X в Y влечет за собой наличие стрелки из Y в X.

4) R называется асимметричным, если из того, что x связан отношением R с y, следует, что y не связан отношением R с x.

( )

5) R называется антисимметричным, если из того, что x связан отношением R с y, а y связан отношением R с x, следует, что х=у.

( )

6) R называется транзитивным, если из того, что x связан отношением R с y, а y связан отношением R с z, следует, что x связан отношением R с z.

( )
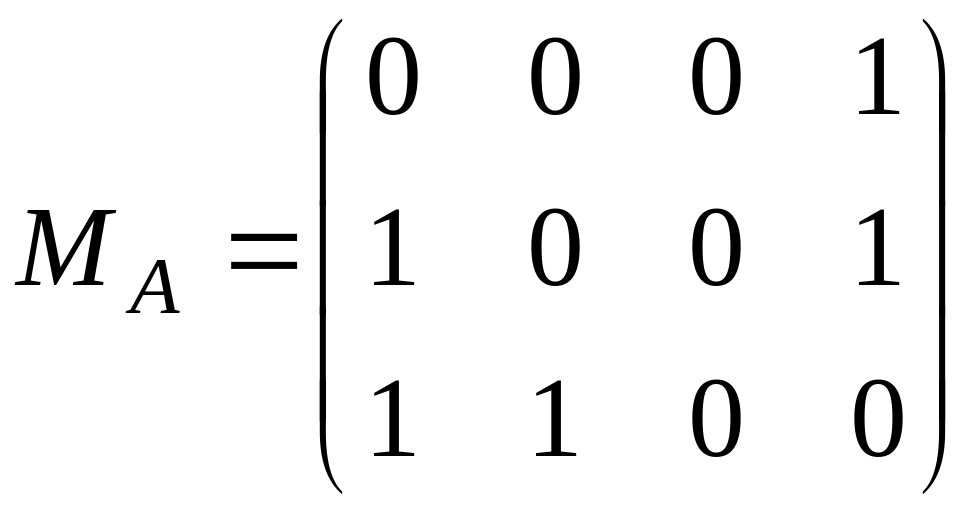