9.4. Зависимость между булевыми функциями

Из таблицы 9.1 видно, что между функциями имеется зависимость:

Из этих зависимостей следует, что любая функция двух перемен­ных (включая константы) выражается в аналитической форме через совокупность шести функций, содержащей отрицание и любую из каждой пары функций , , , , . Например, такой совокупностью могут служить функции: константа 0, отрицание , конъюнкция , дизъюнкция , эквиваленция и импликация . Эта совокупность функций используется в исчислении высказываний.

Выбранная таким способом совокупность шести функций явля­ется избыточной. Можно показать, что импликация и эквиваленция выражаются через остальные функции этой совокупности:

Для этого достаточно построить таблицу соответствия и срав­нить ее с табл. 9.1:

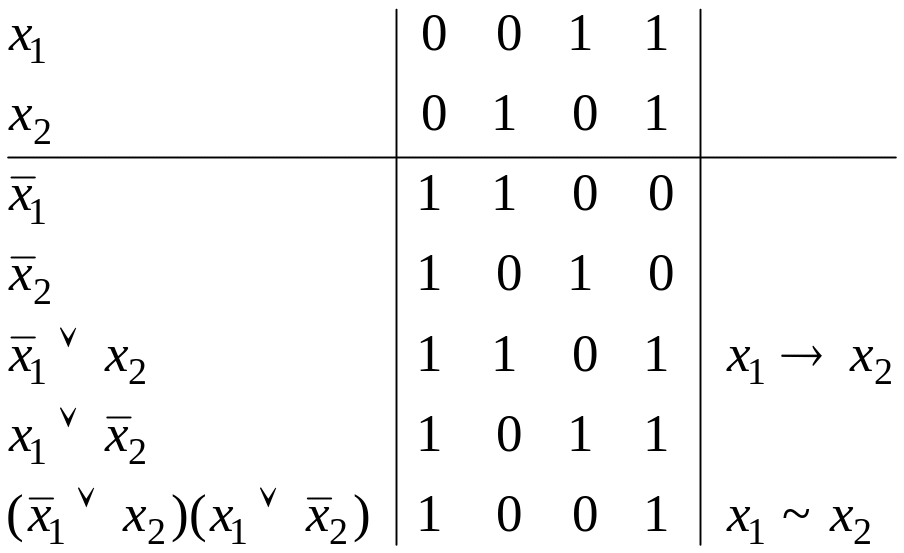
Таким образом, комплект элементарных функций сокращается до четырех: константа 0, отрицание , конъюнкция , дизъюнкция . Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Далее будет показано, что любые булевы функции могут быть выражены через отри­цание и конъюнкцию или через отрицание и дизъюнкцию.

Более того, для записи любой булевой функции достаточно только одной из двух элементарных функций - стрелки Пирса или штриха Шеффера. Это вытекает из следующих соотношений (их доказатель­ство приводится аналогично с помощью таблиц соответствия):

10. Алгебра логики

10.1.Булева алгебра

Множество всех булевых функций вместе с операциями конъюнкции, дизъюнкции и отрицания образует булеву алгебру. На основе определения основных операций можно убедиться в справедливости следующих тождеств булевой алгебры:

- коммутативность
- ассоциативность
- дистрибутивность
- свойства констант
- свойства отрицания

Приведенные свойства позволяют получить ряд других важных законов:

-закон двойного отрицания
- законы де Моргана
- законы идемпотентности
- законы поглошения

Использование этих тождеств существенно упрощает запись логических формул.

10.2. Двойственность формул булевой алгебры

Из свойств, при­веденных в (10.1), видно, что в булевой алгебре, как и в алгебре множеств, имеет место, принцип двойственности. Взаимно двой­ственными операциями являются дизъюнкция и конъюнкция. За­меняя в некоторой формуле каждую операцию на двойственную ей, получаем двойственную формулу. Например, из формулы имеем .

На основе законов де Моргана выводится следующее положение: если и - двойственные формулы, то равносильна . Отсюда следует, что

=

т. е. двойственная формула выражается как отрицание формулы, полученной из исходной замещением каждой переменной ее отри­цанием. Таблица соответствия двойственной функции получается заменой аргументов и значений в исходной функции на противополож­ные, т. е. 0 заменяется на 1, а 1 - на 0. Если формулы и равносильны, то и двойственные им формулы и также равносильны.

Формула или функция, равносильная своей двойственной, называется самодвойственной. Самодвойственная функция на инверсных наборах принимает инверсные значения.