7.5. Поле комплексных чисел

Комплексное число , где - действительная часть и - мнимая часть, можно рассматривать как упорядоченную пару (а, b) двух действи­тельных чисел, которые являются элементами множества R.

На множестве комплексных чисел определяются два внутрен­них закона - сложение и умножение:

; .

Два числа z₁ и z₂ равны, если a₁ = a₂ и b₁ = b₂.

В принятых обозначениях i = (0,1), следовательно, i² = (0,1)(0,1) = (-1,0) или i² = -1. Действия над комплексными числами в форме можно выполнять как с действитель­ными числами, заменяя всякий раз i² на -1.

Числом, комплексно-сопряженным с числом г = а + bi, является число . Справедливы следующие соотношения:

.

Множество комплексных чисел составляет коммутативную группу относительно сложения. Действительно, сложение комму­тативно и ассоциативно, нейтральным элементом служит нуль (0, 0), а симметричное числу есть .

Относительно умножения нейтральным элементом является единица (1, 0), и всякое отличное от нуля комплексное число имеет симметричное (обратное)

,

где - модуль комплексного числа. Т.к. умноже­ние дистрибутивно относительно сложения, то множество комплекс­ных чисел составляет поле.

Указанное представление называется представлением комплексного числа в алгебраической форме. Комплексное число представляется также в тригонометрической и экспоненциальной форме:

Здесь - модуль и  - аргумент комплексного числа, определяемый с точностью до целого кратного 2π, причем .

Указанное представление удобно для вычисления произведения двух комплексных чисел:

.

Таким образом, и .

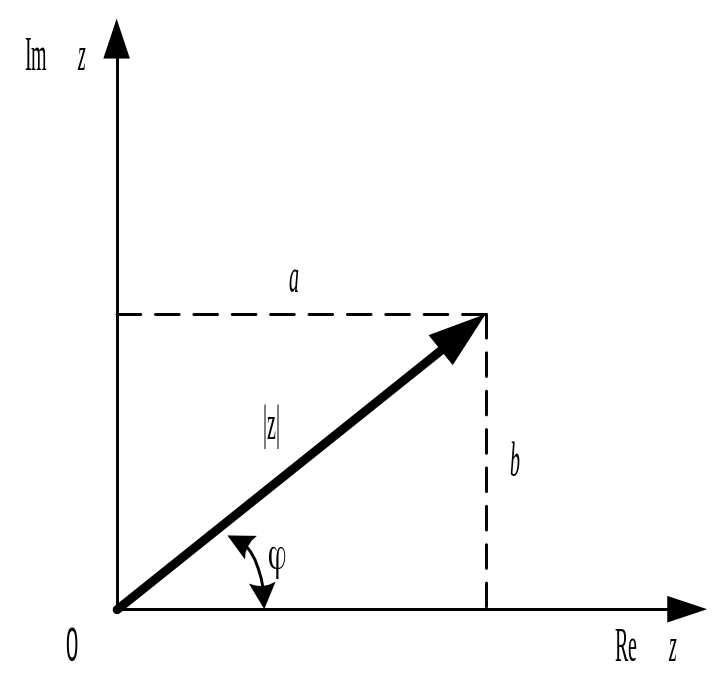
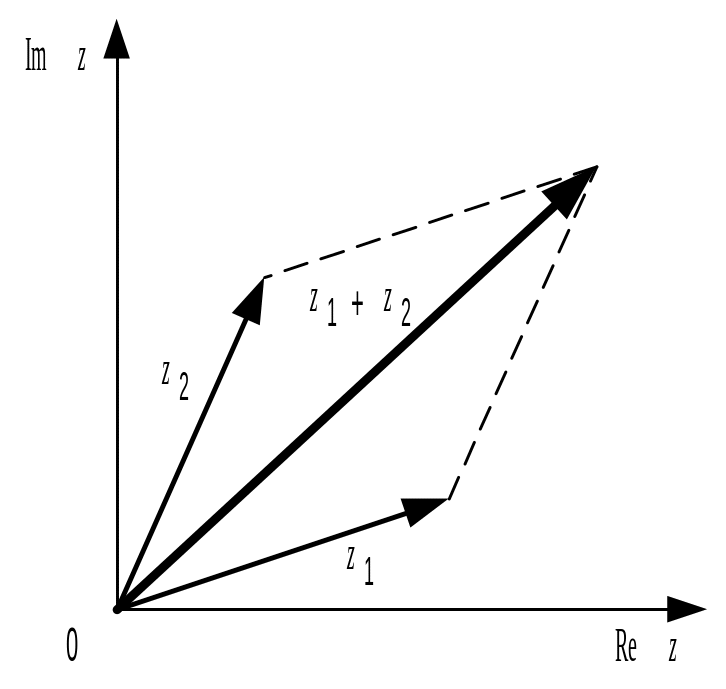
Геометрически представление комплексных чисел представлено на рис. 7.1а. Суммированию комплексных чисел соответствует геометрическое сложение векторов на комп­лексной плоскости (рис. 7.1б). Отсюда, в частности, следует (правило треугольника).

а)	б)
Рис. 7.1. Геометрическое представление комплексных чисел

7.6. Тело кватернионов

Первой системой на пути обобщения комплексных чисел явились кватернионы, т. е. выражения вида , где а, b, с, d - действительные числа, а символы i, j, k также называют кватернионами. Число а - действи­тельная часть, а сумма - векторная часть кватер­ниона.

На множестве кватернионов определяют два внутренних закона. Аддитивный закон задается подобно сложению комплекс­ных чисел, т.е. сумма кватернионов и есть

.

Очевидно, этот закон ассоциативный и коммутативный. Нейтраль­ным элементом относительно сложения служит , а симметричным к элементу q есть элемент .

Чтобы множество кватернионов было телом, мультипликатив­ный закон (умножение кватернионов) должен быть ассоциативным и дистрибутивным относительно сложения. Это достигается, с одной стороны, определением мультипликативного закона подобно умно­жению многочленных алгебраических выражений и, с другой сто­роны, заданием правила умножения кватернионов, которое в наи­более лаконичной записи имеет вид:

,

где порядок сомножителей в произведении ijk строго фиксирован. Отсюда также следует

.

Действительно, умножая справа на k обе части равенства ijk = -1, имеем ijk² = -k или ij = k. Умножая полученное уравнение на j справа или на i слева, получаем соответственно -i = kj или -j = ik и т. д.

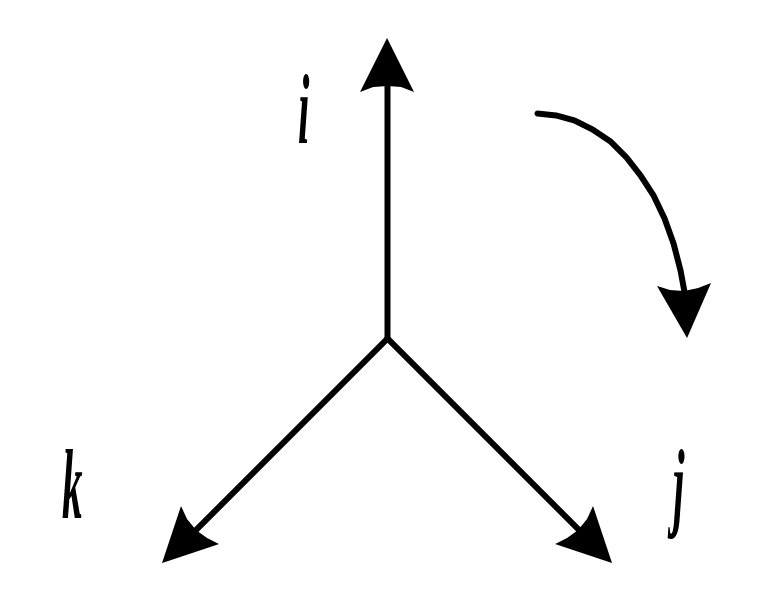
Геометрически умножение кватернионов легко представить с помощью диаграммы (рис. 7.2): произведение двух кватернионов равно третьему со знаком «+», если поворот от первого сомножителя ко второму осуществляется по часовой стрелке, и со знаком «-», если поворот против часовой стрелки.

Рис.7.2. Умножение кватернионов

Нетрудно проверить, что мультипликативный закон (умножение кватерни­онов) не коммутативный (проверяется непосредственным умножением с учетом изложенных выше правил). Нейтральным элементом относительно умножения служит еди­ница, рассматриваемая как кватернион, у которого а = 1 и b = с = d = 0. Можно также показать, что относительно умножения каждый кватернион имеет симметричный (обратный) ему

,

где число называют нормой кватерниона. Итак, множество кватернионов, наделенное описанными выше двумя внутренними законами компо­зиции, образует тело.

В механике кватернионы применяются при решении задач, связанных с вращениями твердого тела в пространстве.