5.8. Графы отношений порядка

Граф нестрогого порядка не содержит параллельных и противоположно направленных дуг, с каждой вершиной связана петля, а также все вершины любого пути попарно связаны между собой дугами и направлении этого пути. Граф строгого порядка отличается тем, что отсутствуют петли, а граф квазипорядка - тем, что допускает параллельные и противоположно направленные дуги.

Так как отношение порядка транзитивно, то его граф обычно •вменяется графом редукции, причем в графе нестрогого порядка петли не изображаются. Граф квазипорядка можно упростить, заменив его графом строгого порядка на множестве вершин, соответствующих классам эквивалентности. При этом каждая такая вершина изображает все множество элементов данного класса.

На рис. 5.1 показан упрощенный граф отношения «быть делителем» из (9). На графе наглядно прослеживается структура упорядоченного множества. Так, для подмножества Q = {4, 6, 14, 28, 42} мажорантой является элемент 84, а минорантами - элементы 1 и 2. Максимума и минимума Q не имеет, но sup Q = 84, inf Q = 2. Для всего множества единственная мажоранта 84 является одновременно максимальным элементом, а миноранта 1 - минимальным элементом.

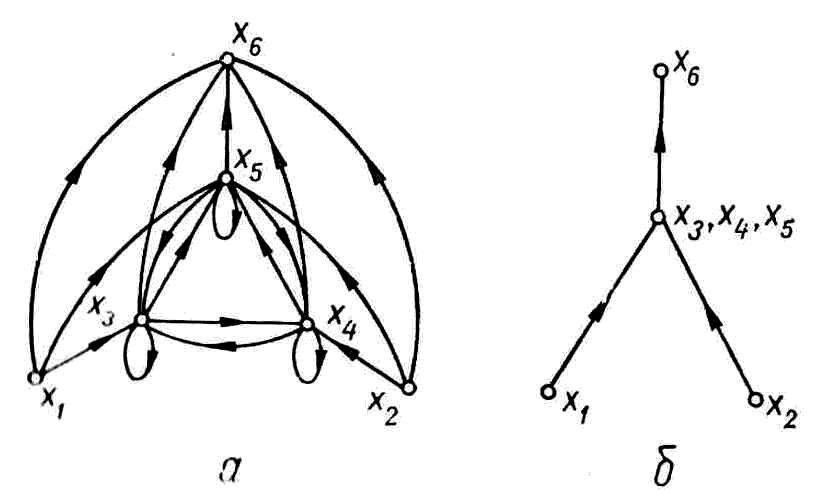
На рис. 5.2, а показан граф отношения квазипорядка, a на рис. 5.2, б - упрощенный граф отношения порядка на множестве классов эквивалентности индуцированного этим квазипорядком.

Совершенный порядок всегда представляется связным графом, в то время как граф частичного порядка может быть несвязным.


Рис. 5.1. Упрощенный граф отношения «быть делителем»	Рис. 51. Граф отношения квазипорядка (а) и его упрощенное изображение (б).

6. Законы композиции

6.1. Композиция объектов. Таблица Кэли.

В математике и ее приложениях большое значение имеют отношения, ставящие в соответствие паре каких-либо объектов (а, b) третий объект с. Примерами таких отношений являются действия над числами. В общем случае отношение может представлять собой некоторую операцию не только между числами, но и между объектами любой природы. Запись a┬b=c (a┴b=c) означает, что а в композиции c b дает с. Символ ┬ (┴) обозначает операцию, объекты а и b называют операндами, а объект с – результатом операции или композицией объектов а и b.

Обозначим множества операндов соответственно через А и В (aA, bB), а множество результатов операции — через С (сС). Так как множество всех пар (а, b) есть прямое произведение , то операцию определяют как отображение множества в С, т. е. , и часто называют законом композиции.

Любой закон композиции над конечными множествами можно задавать прямоугольной матрицей (таблицей Кэли). Строки таблицы соответствуют элементам множества А, столбцы - элементам множества В. На пересечении строки и столбца, соответствующих паре (а, b), располагается элемент с= a┬b. Хорошо известными примерами являются таблицы сложения и умножения одноразрядных чисел. В общем случае таблица, определяющая бинарную операцию, имеет вид: