Задание 2

Для решения первой задачи задания записываем исходные данные с общепринятыми обозначениями:

N = 159,2 млн р. – суммарная стоимость ОПФ по генеральной совокупности; n = 15,92 млн р. – суммарная стоимость ОПФ по выборочной совокупности; P = 0,997 млн р. – вероятность; t = 3 млн р. – коэффициент доверия.

Затем на основании ранее выполненной аналитической группировки записываем в группировочную таблицу необходимую исходную информацию для расчета средней ошибки выборки 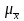(табл. 5.1):

Исходные данные для расчета средней ошибки выборки.

Таблица 5.1

Группы предприятий по среднегодовой стоимости ОПФ, млн р.	Число предприятий в группе, ед. Fi	Серединное значение ОПФ в группе X'i	Стоимость ОПФ по группе x'fi
3,7…5,4	4	4,5	18
5,4…7,1	5	6,2	31
7,1…8,8	2	7,9	15,8
8,8…10,5	5	9,6	48
10,5…12,2	4	11,3	45,2
Итого	20	-	158

Для расчета среднегодовой стоимости ОПФ по генеральной совокупности необходимо вначале оценить репрезентативность выборки. Для этого рассчитываем среднюю и предельную ошибки выборки.

Расчет средней ошибки выборки производим двумя способами в зависимости от процедуры проведения выборки – повторный отбор или бесповторный.

В первом случае используется формула:

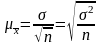
во втором:

,

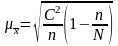где С² – выборочная дисперсия; N – число единиц генеральной совокупности; n – число единиц выборочной совокупности.

Выборочную дисперсию определяем по формуле:

,

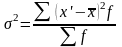где x’ – среднее значение ОПФ в группе; - среднее значение ОПФ по выборке; - число предприятий в группе.

Среднее значение ОПФ по выборке находим из выражения:

= 7,9

Тогда:

= 6,1

0,62

Предельная ошибка выборки при P = 0,997 и t = 3 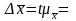1,86

Пределы генеральной средней при заданной вероятности (P = 0,997) составляют:

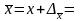7,9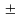 1,86, т.е. 6,04млн р.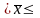 9,76млн р.

Следовательно, с вероятностью 0,997 можно утверждать, что среднегодовая стоимость ОПФ в генеральной совокупности находится в пределах от 6 до 9,6млн р.

При бесповторном отборе результаты будут иные, а именно:

средняя ошибка выборки: 0,58

предельная ошибка выборки: 1,74

пределы генеральной средней 7,9 1,74,т.е. 6,16млн р. 9,64млн р.

Следовательно, пределы генеральной средней в этом случае несколько меньше, чем при повторном отборе.

Решение второй части задачи, т.е. определение вероятности того, что генеральная средняя будет отличаться от выборочной средней не более чем на 1 млн р., производится в следующей последовательности.

Из условий задачи следует, что предельная ошибка выборки 1 млн р.

Используя выражение 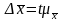, можно записать в случае повторного отбора 1,0 = t0,62. Тогда t = 1,61.

По таблице значений функции Лапласа Ф(t) = P[T]≤t_табл. при различных значениях t находим P = 0,8926.

В случае бесповторного отбора 1,0 = t0,58. Тогда t = 1,72; P = 0,9127.

Таким образом, с вероятностью соответственно 0,8926 и 0,91927можно гарантировать, что среднегодовая стоимость ОПФ в генеральной совокупности будет не менее 6,04млн р., но не более чем 9,76млн р. при повторном отборе и не менее 6,16млн р., но не более 9,64млн р. при бесповторном отборе.