Навантаження від снігу.
Снігове
навантаження визначаємо згідно ДБН
В.1.2-2-2006 “Навантаження і впливи”.
Характеристичне значення ваги снігового
покриву для м. Червнівці розташованого
в ІV зоні згідно [3, Рисунок 8.1], становить
Граничне розрахункове значення снігового навантаження на горизонтальну проекцію покриття обчислюємо за формулою:
де
коефіцієнт надійності за граничним
розрахунковим значенням снігового
навантаження, визначається в залежності
від заданого середнього періоду
повторюваності. Для об’єктів масового
будівництва допускається середній
період повторюваності приймати таким,
що дорівнює встановленому періоду
експлуатації конструкції
.
Період експлуатації
приймаємо згідно чинного ДБН В.1.2-14,
(п.5.3).
де
коефіцієнт переходу від ваги снігового
покриву на поверхні грунту до снігового
навантаження на покрівлю [3, дод. Ж, сх.1];
коефіцієнт,
що враховує режим експлуатації покрівлі,
при відсутності про режим експлуатації
, допускається приймати таким, що дорівнює
одиниці.
коефіцієнт
географічної висоти,який враховує
висоту розміщення будівельного об’єкта
над рівнем моря. Оскільки планувальна
відмітка споруди становить 339,3 м, що
менше 0,5 км., то коефіцієнт приймаємо
рівним одиниці.
Експлуатаційне розрахункове значення обчислюємо за формулою:
де
коефіцієнт надійності за експлуатаційним
значенням снігового навантаження,
визначаємо за таблицею залежно від
частки часу
протягом якої можуть порушуватися умови
другого граничного стану. Значення η
приймається за нормами проектування
або встановлюється завданням на
проектування залежно від їхнього
призначення, відповідальності та
наслідків виходу за граничний стан. Для
об’єктів масового будівництва
допускається приймати
при
такому значенні коефіцієнта η,
те
саме, що і в попередній формулі.
Таким
чином, розрахункове граничне снігове
навантаження на покриття обчислюємо
за формулою (8.1) Норм [2]:
Граничне
розрахункове постійне навантаження на
1 м з урахуванням власної ваги арки
.
Геометричні характеристики та зусилля в перерізах арки.
Арку розраховуємо як двошарнірну із затяжкою.(рис. 1)
Знаходимо геометричні характеристики арки згідно рис. 2:
Радіус осі кругової арки
Де f – стріла підйому прийнята рівною 1/9 прольоту.
Центральний кут
Довжина арки
Де
Розбиваємо
арку на 10 рівних частин (дузі 0,1 частини
відповідає кут
)
і визначаємо горизонтальні координати
січень за формулами:
Де
П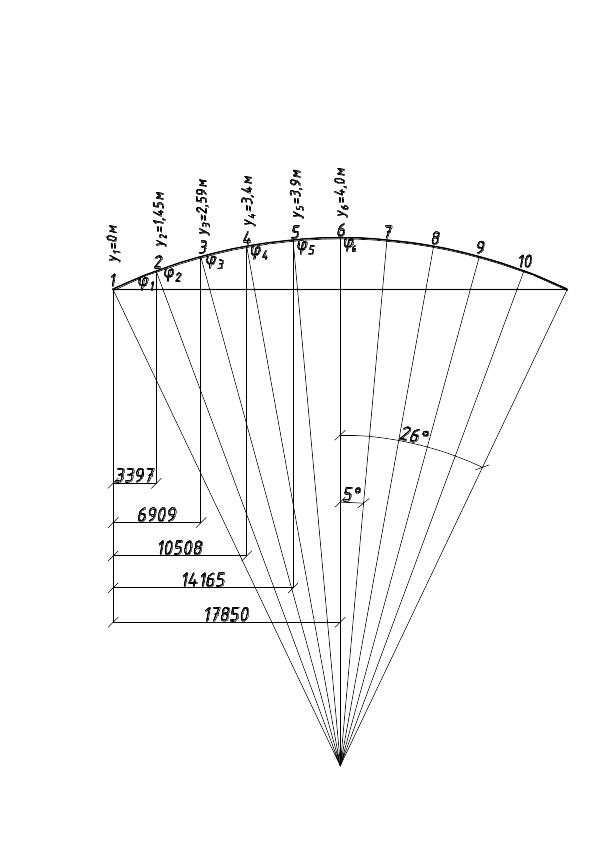
ри
При
При
При
Рис. 3.1. Геометрична схема арки
При 
Величина
,
відповідає
довжині стріли підйому
Попередньо задаємося площею арматури в арці та в затяжці, а також обчислюємо характеристики їх січень.
Приймаємо
приблизно для арки
.
Приймаємо
Відношення модулів пружності для арки:
Тоді площа приведеного симетричного армування січення арки:
Момент
інерції приведеного січення при відстані
до центру тяжіння
см.
.
Радіус інерції приведенного січення
Приймаємо
площу затяжки
і приблизно приймаємо площу арматури:
Прийнявши
до уваги те, що відношення
модулів пружності
визначаємо площу приведеного перерізу
затяжки
Коефіцієнт податливості затяжки
Для
кожного
випадку завантаження знаходимо розпір
від навантаження
, прийнятого за одиничне: для
рівномірно розподіленого навантаження.
Для одностороннього рівномірно розподіленого навантаження на половині прольоту арки:
За розрахованим розпором для кожного виду завантаження знаходимо розрахункові зусилля в січеннях арки.
При рівномірно розподіленому навантаженні балочні моменти і поперечні сили знаходимо за формулами:
Де
– опорна
реакція в балці.
Наприклад
при
м(
і
/м)
При завантаженні половини прольоту арки балочний момент і поперечну силу в не загруженій частині визначаємо за формулою:
Де
–реакція
в балці зі сторони незагруженої частини.
Наприклад
при
м(
і
/м)
Після обчислення балочних моментів і поперечних сил по приведених нижче формулах обчислюємо зусилля для всіх перерізів арки:
Де
φ – кут між
дотичною
до осі
арки та горизонталлю;
та
–згинаючий
момент та поперечна сила в балці на двох
опорах з прольотом рівним
розрахунковому
прольоту
арки.
Визначаємо
Mx
,Nx
,Vxв
середині прольоту арки при дії рівномірно
розподіленого навантаження
/м
при φ=0 ; Mо
;
;
H=19,2кН
; y6
Зусилля від одиничного навантаження /м розподіленого по всій довжині прольоту.
Номер січення |
|
|
, |
|
|
|
|
|
|
|
1 |
39 |
0,00 |
0,00 |
0,00 |
35,02 |
0,00 |
0,00 |
0,00 |
0,43 |
0,898 |
2 |
54,87 |
14,45 |
-1,68 |
41,56 |
0,23 |
3,397 |
1,45 |
0,342 |
0,939 |
|
3 |
99,46 |
10,94 |
-1,55 |
40,50 |
0,51 |
6,909 |
2,59 |
0,258 |
0,966 |
|
4 |
132,36 |
7,34 |
-0,24 |
39,64 |
1,16 |
10,508 |
3,4 |
0,156 |
0,987 |
|
5 |
152,52 |
3,69 |
0,42 |
36,15 |
0,99 |
14,165 |
3,9 |
0,069 |
0,997 |
|
6 |
159,31 |
0,00 |
3,31 |
39,0 |
0,00 |
17,85 |
4,00 |
0,00 |
1,00 |
|
7 |
152,52 |
3,69 |
0,42 |
36,15 |
0,99 |
14,165 |
3,90 |
0,069 |
0,997 |
|
8 |
132,36 |
7,34 |
-0,24 |
39,64 |
1,16 |
10,508 |
3,40 |
0,156 |
0,987 |
|
9 |
99,46 |
10,94 |
-1,55 |
40,50 |
0,51 |
6,909 |
2,59 |
0,258 |
0,966 |
|
10 |
54,87 |
14,45 |
-1,68 |
41,56 |
0,23 |
3,397 |
1,45 |
0,342 |
0,939 |
|
11 |
0,00 |
0,00 |
0,00 |
35,02 |
0,00 |
0,00 |
0,00 |
0,43 |
0,898 |
,
,
,
,
Зусилля від одиничного навантаження /м розподіленого на лівій половині арки.
Номер січення |
, |
|
, |
, |
, |
, |
|
|
|
|
1 |
19,5 |
0,00 |
8,45 |
0,00 |
21,15 |
-0,8 |
0,00 |
0,00 |
0,43 |
0,898 |
2 |
15,15 |
6,96 |
-4,35 |
20,63 |
-0,15 |
3,397 |
1,45 |
0,342 |
0,939 |
|
3 |
30,82 |
5,47 |
11,32 |
20,25 |
0,25 |
6,909 |
2,59 |
0,258 |
0,966 |
|
4 |
46,87 |
3,98 |
27,37 |
19,87 |
0,89 |
10,508 |
3,4 |
0,156 |
0,987 |
|
5 |
63,18 |
1,49 |
43,68 |
19,54 |
0,14 |
14,165 |
3,9 |
0,069 |
0,997 |
|
6 |
79,61 |
-4,46 |
60,11 |
19,39 |
-4,46 |
17,85 |
4,00 |
0,00 |
1,00 |
|
7 |
63,18 |
-4,46 |
43,68 |
19,13 |
-5,79 |
14,165 |
3,90 |
0,069 |
0,997 |
|
8 |
46,87 |
-4,46 |
27,37 |
13,39 |
-7,44 |
10,508 |
3,40 |
0,156 |
0,987 |
|
9 |
30,82 |
-4,46 |
11,32 |
17,69 |
-9,34 |
6,909 |
2,59 |
0,258 |
0,966 |
|
10 |
15,15 |
-4,46 |
-4,35 |
16,79 |
-10,36 |
3,397 |
1,45 |
0,342 |
0,939 |
|
11 |
0,00 |
-4,46 |
0,00 |
15,59 |
-12,39 |
0,00 |
0,00 |
0,43 |
0,898 |
Для знаходження розрахункових зусиль в січенних арки необхідно для кожного виду завантаження величин ,що приведені в табл. 1 та табл. 2, домножити на перевідні коефіцієнти:
Для постійного навантаження
Для тимчасового навантаження
В табл. 3 приведені значення зусиль від всіх видів завантажень, а також розрахункова комбінація зусиль при найбільш невигідному їх поєднанні 1,5,6,10,11.
Розпір
від розрахункового навантаження при
.
Схема завантаженн |
Вид зусиль |
Січення арки |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
||
q=31,2 H=737,09 |
M , кН∙м |
0.00 |
6.60 |
3.84 |
30.48 |
34.63 |
27.64 |
34.63 |
30.48 |
3.84 |
6.60 |
0.00 |
N , кН |
808.11 |
784.69 |
764.73 |
746.69 |
737.47 |
737.09 |
737.47 |
746.69 |
764.73 |
784.69 |
808.11 |
|
V , кН |
-11.90 |
1.54 |
6.91 |
6.53 |
-11.90 |
0.00 |
-11.90 |
6.53 |
6.91 |
1.54 |
-11.90 |
|
s=15,62 H=282,43 |
M , кН∙м |
0.00 |
2.53 |
1.47 |
11.68 |
13.27 |
10.59 |
13.27 |
11.68 |
1.47 |
2.53 |
0.00 |
N , кН |
309.65 |
300.67 |
293.02 |
286.11 |
282.58 |
282.43 |
282.58 |
286.11 |
293.02 |
300.67 |
309.65 |
|
V , кН |
-4.56 |
0.59 |
2.65 |
2.50 |
-4.56 |
0.00 |
-4.56 |
2.50 |
2.65 |
0.59 |
-4.56 |
|
Одностороннє завантаження s=15,62 H=141,42 |
M , кН∙м |
0.00 |
16.49 |
33.98 |
58.28 |
-17.03 |
2.79 |
-17.03 |
-32.12 |
-28.33 |
-23.99 |
0.00 |
N , кН |
108.59 |
99.46 |
86.92 |
78.33 |
74.85 |
74.30 |
72.91 |
70.67 |
67.34 |
63.93 |
59.37 |
|
V , кН |
42.42 |
33.98 |
25.08 |
12.69 |
7.51 |
-17.11 |
-22.21 |
-28.48 |
-35.68 |
-41.49 |
-47.29 |
|
H=1019,52 |
max , min M |
0 |
23.09 |
37.82 |
88.76 |
47.9 |
38.23 |
47.9 |
42.16 |
5.31 |
9.13 |
0 |
відпов.N кН |
916.7 |
884.15 |
851.65 |
825.02 |
812.32 |
811.39 |
810.38 |
817.36 |
832.07 |
848.62 |
867.48 |
|
max N,кН |
1117.76 |
1085.36 |
1057.75 |
1032.8 |
1020.05 |
1019.52 |
1020.05 |
1032.8 |
1057.75 |
1085.36 |
1117.76 |
|
відпов.M,кН |
0 |
9.13 |
5.31 |
42.16 |
17.6 |
30.43 |
17.6 |
-1.64 |
-24.49 |
-17.39 |
0 |
|
max V , кН |
30.52 |
35.52 |
31.99 |
19.22 |
-16.46 |
-17.11 |
-34.11 |
-21.95 |
-28.77 |
-39.95 |
-59.19 |
|
Розрахунок затяжки на міцність
Арматуру затяжки підбираємо як для центрально розтягненого елемента за умовами міцності.
Розраховуємо необхідну площу арматури
Коефіцієнт
.
Число прутів при
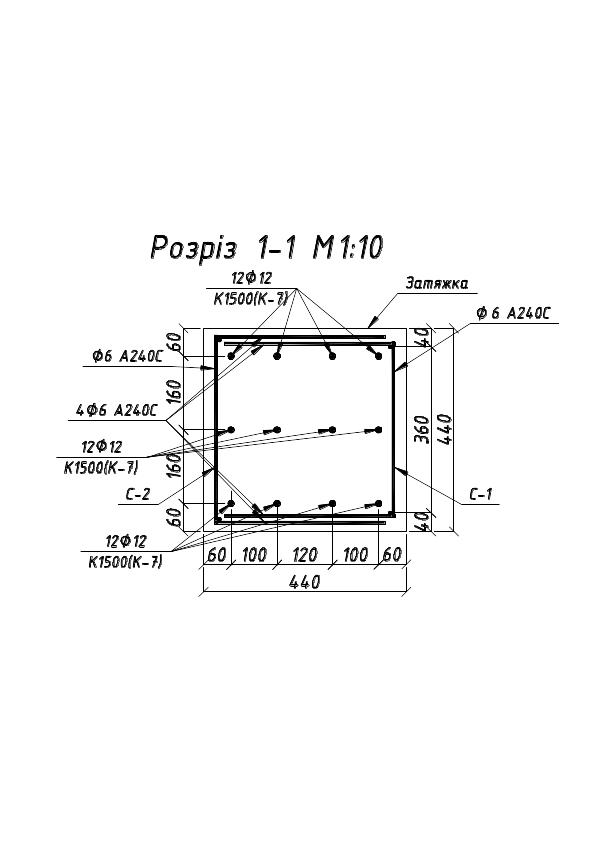
Рис.5.1. Армування затяжки
Приймаємо 12 стержнів.
