1. Структура системы цифровой обработки сигналов. Влияние формы дискретизирующих импульсов на спектр дискретизированного сигнала.

ФНЧ ПНС – ФНЧ, Предотвращающий Наложение Спектров.

ФНЧ В – ФНЧ-восстановитель.

- сумма спектров сдвинутых сигналов.2/T=(дискр)

- спектр импульсов дискретизации.

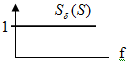
Спектр дискретизированного сигнала при произвольной форме импульсов дискретизации, отличается от спектра при дискретизации при произвольной δ-функции дополнительным множителем S0(ω), описывающим спектр импульсов дискретизации.

Импульсы конечной длительности затухают с ростом частоты – это приводит к мультипликативным искажениям спектра дискретизированного сигнала.

Пример: импульсы дискретизации прямоугольной формы:

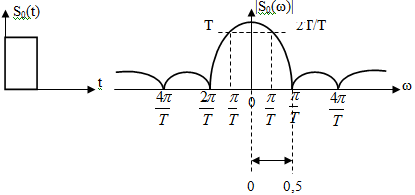
Спектр прямоугольных импульсов определяется по формуле:

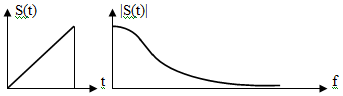
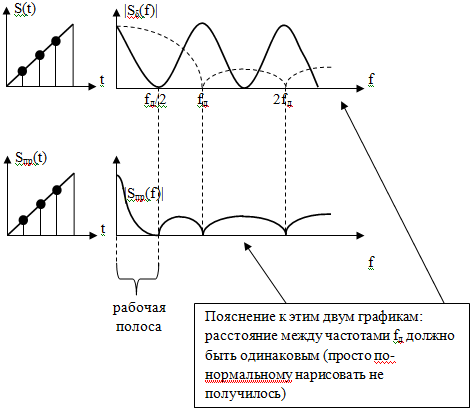
Спад амплитудного спектра на частоте w=/T составляет:

В середине рабочей полосы сигнал ослабляется примерно на 4 дБ.

Следствия:

1) ЦАП, как правило, выдаёт импульсы прямоугольной формы и фактически является ФНЧ с большой неравномерностью в полосе пропускания и с недостаточным проявлением в полосе задерживания.

2) Для применения некритичных к качеству сигналов, фильтр-восстановитель можно не использовать.

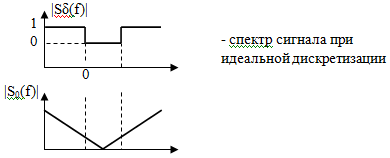
Задача: Найти спектр реальной дискретизации |Sреал(f)|.

2. Z-преобразование.

Следующий пункт я-ся примером к z –преобр.-ю

3.Разностные уравнения для описания дискретных систем. Нерекурсивная и рекурсивная цифровая фильтрация.

Структурные схемы цифровых фильтров

Разностным уравнением наз-ся выражение:

y – отсчеты выходного сигнала

a и b – постоянные коэффициенты

запись x(k i) или y(k i) означает задержку сигнала на i тактов.

Разностное уравнение определяет алгоритм работы дискретной системы.

Дискретный фильтр – произвольная система обработки

дискретного сигнала, обладающая свойствами линейности и стационарности.

Линейность означает, что выходная реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности, а стационарность – что задержка вх. с-ла

приводит лишь к такой же задержке вых. с-ла , не меняя его формы.

В нерекурсивном фильтре для вычисления вых. отсчета используется только вх. отсчеты.

В рекурсивном фильтре, кроме того, используются задержанные отсчеты вых. с-ла.

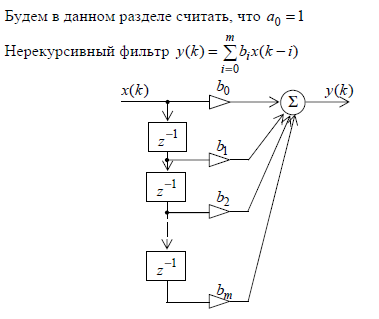
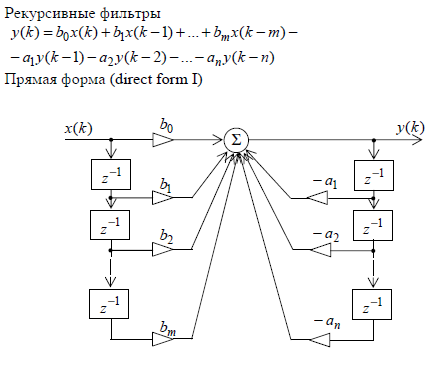
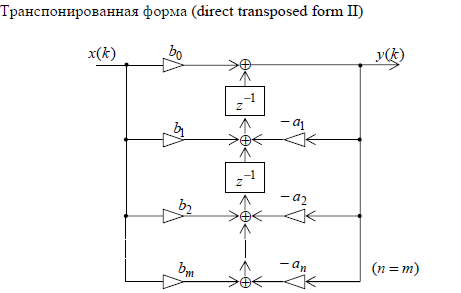
Транспонированная схема позволяет эффективно распараллелить вычисления. При реализации фильтра в прямой или канонической форме можно одновременно выполнять все операции умножения, но для получения выходного результата необходимо

дождаться выполнения всех операций сложения. В транспонированной же схеме, помимо умножения, можно одновременно выполнять и все операции сложения, поскольку они являются независимыми.

4. Свертка дискретных сигналов: линейная и круговая свертка. Привести примеры вычисления линейной и круговой свертки.

Круговая свертка. Если Х1(n) и Х2(n)-периодические сигналы с периодом N, то их круговая свертка определяется выражением:

Круговую свертку можно вычислить с использованием ДПФ по следующему алгоритму:

1. Вычислить ДПФ X1(k) и X2 (k) для x1(n) и x2 (n)

2. Вычислить ДПФ Y(k) X1(k)X2 (k) для свертки y(n) ;

3. Вычислить y(n) с помощью ОДПФ.

Как правило, ДПФ и ОДПФ вычисляют с помощью БПФ. Пример: Х1(n) = {1; 2; 3} и Х2(n)={4; 5; 6}

Y(0) = Х1(0)*Х2(0)+ Х1(1)*Х2(-1)+ Х1(2)*Х2(-2)

Y(1) = Х1(0)*Х2(1)+ Х1(1)*Х2(0)+ Х1(2)*Х2(-1)

Y(2) = Х1(0)*Х2(2)+ Х1(1)*Х2(1)+ Х1(2)*Х2(0)

Линейная свертка. Х1(n) и Х2(n) сигналы длиной N1 и N2.

Максимальное количество символов : N1 + N2 -2. Длина свертки : N1 + N2 -1

Пример: Х1(n) = {1; 2} и Х2(n)={3; 4; 5}

Y(0) = Х1(0)*Х2(0)= 3

Y(1) = Х1(0)*Х2(1)+ Х1(1)*Х2(0)= 4+6=10

Y(2) = Х1(0)*Х2(2)+ Х1(1)*Х2(1)+ Х1(2)*Х2(0)=5+8=13

Y(3) = Х1(0)*Х2(3)+ Х1(1)*Х2(2)+ Х1(2)*Х2(1) + Х1(3)*Х2(0)=0+10+0+0=10