Расчетно-графическое задание

Исследование корректности применения построенных разными методами доверительных интервалов для прогноза временного ряда при различных исходных распределениях значений временного ряда

Исходные данные и формализация задачи

Введение. Понятие о сезонных индексах.

Рассматриваются данные временных рядов, полученных в результате наблюдения за некоторыми реальными объектами (например, помесячный объем выручки пивоваренного завода, объем продаж киоска с мороженным). Предполагаем, что во временном ряде не наблюдается долгосрочной тенденции, но имеют место периодические изменения. В этом случае модель временного ряда должна содержать в себе функцию сезонности. Для построения функции сезонности существует множество подходов, но все они предполагают, что функция является периодической. Часто период сезонной функции можно определить из постановки задачи. Например, при рассмотрении ежеквартальных данных по потреблению тепловой энергии, очевидно, что период сезонных колебаний равен году, а количество сезонов . Если же данные по потреблению тепловой энергии представлены за каждый месяц, то период по-прежнему равен одному году, а количество сезонов . Предполагаем, что у нас в наличии имеются данные за пять периодов. Причем данные представлены не в исходном, а уже в некотором агрегированном виде.

В качестве примера на рис.1 показаны объемы потребления кефира в некотором супермаркете для каждого года и среднее значение за 5 лет. Год равен дробному количеству 52,14 недель, но для упрощения расчетов он полагался равным целому числу 52 неделям, а неполная последняя неделя года переносилась на первую неделю следующего. То есть в данном случае .

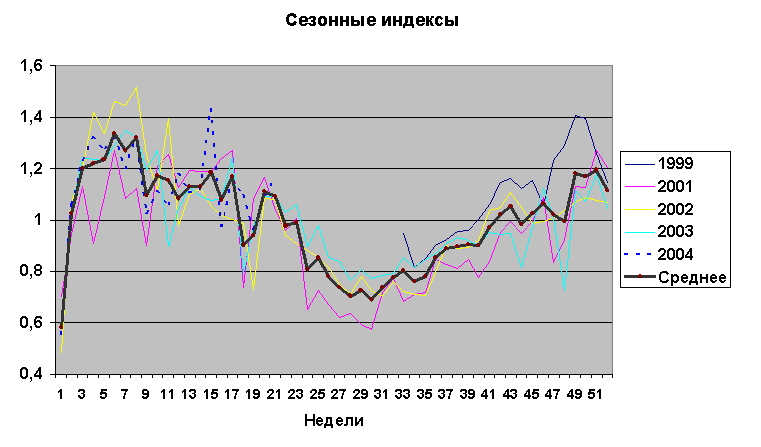
Рисунок 1.

В задании на РГЗ будет дана информация именно об усредненных индексах (соответствует темной толстой линии на рисунке), и в данной работе мы рассматриваем самый простой способ задания функции сезонности – табличный.

Табличное представление сезонной функции

Номер сезона	1	2	…	Р
Сезонный индекс			…

Традиционно предполагают, что все сезонные воздействия за период взаимопогашаются:

.

Учитывая это условие и принимая во внимание тот факт, что реальные временные ряды, как правило, имеют ненулевые математические ожидания, целесообразно рассматривать модель вида

(другая общепринятая форма записи этой же модели - ).В этой модели - нерегулярная, случайная составляющая временного ряда. Обычно предполагают, что это независимые(при различных значениях ) величины, подчиняющиеся нормальному закону распределения с нулевым математическим ожиданием и некоторой известной дисперсией.

Оценивание сезонных индексов как средних отклонений элементов временного ряда от оценки математического ожидания осуществляется согласно формуле:

Где - множество моментов времени, соответствующих -му сезону, - количество элементов в множестве , - оценка математического ожидания временного ряда.

Предположения о дисперсии моделируемых величин в виде регрессионной модели

Дисперсия случайной составляющей временного ряда определяет степень разброса фактических значений ряда вокруг . Из практических наблюдений можно сделать вывод, что дисперсия, взятая как доля от среднего, часто отражает реальную ситуацию – поскольку при малых в среднем объёмах, скажем, потребления и изменчивость вокруг этих значений невелика, и, наоборот, – при увеличении объёма потребления и изменчивость растёт. Из этих соображений, а также для того, чтобы при моделировании избежать парадоксальных ситуаций, скажем, отрицательного потребления, будем полагать дисперсию наблюдений, равной . В приведённой формуле хоть и не используется обозначение оценки дисперсии , а истинной оценки , но на самом деле мы полагаем, что данное значение получено как оценка по выборке данных за пять периодов наблюдения. Обозначается же оно как истинное, поскольку именно это значение должно быть использовано в качестве дисперсии при моделировании псевдо реальных наблюдений временного ряда. А также чтобы не возникало коллизий с оценкой математического ожидания, полученного уже по смоделированной в рамках выполнения РГЗ выборки. А математическое ожидание берём равным нулю (при моделировании для каждого сезона с номером , для которого проводится моделирование).

Цель и последовательность проводимого в работе исследования

Модели временных рядов строят обычно с основной целью – получения с прогноза на некоторые дальнейшие моменты времени. Нетрудно понять, насколько важно получить корректный прогноз прибыли для любого производящего предприятия. В данной работе рассмотрен один из несложных, но широко используемых методов построения прогноза для временных рядов, в которых общий уровень исследуемого показателя остаётся в целом на одном и том же уровне, наблюдаются только сезонные изменения. В рамках рассмотренной модели прогноз показателя для конкретного сезона определяется как . Но помимо самого значения прогноза, важной характеристика прогноза является его точность – оценка доверительного интервала прогноза для заданной вероятности его осуществления. Практическая сторона точности – это получение нижних и верхних границ области, в которой лежит прогноз, информация, которая может использоваться при построении сценариев «худшего» и «лучшего» развития ситуации, определения объёмов минимального запаса при решении задач логистики и т.д. Но, естественно, как только речь заходит о вероятностях, встаёт вопрос о том, по какому закону распределены .

Классические методы статистического анализа работают обычно в рамках предположения о нормальном законе распределения ошибок наблюдения . В рамках данного предположения, а также, для некоторых методов построения доверительных интервалов, и более сильных предположений, например, о гомоскедастичности , были разработаны методы построения доверительных интервалов прогноза.

И первый этап исследований, проводящихся в рамках РГЗ – это убедиться, что то, что должно работать в рамках выполнения предположений, действительно работает достаточно хорошо.

Однако в жизни довольно редко встречается нормальный закон «в чистом виде». Довольно часто закон распределения бывает несимметричным, могут встречаться выбросы, иногда даже двумодальные распределения ошибок наблюдения. Например, в мае выручка завода по производству пива будет сильно различаться в зависимости от того, теплый май или холодный. То есть завод может или совсем прогорать в этом месяце, или иметь сверхприбыль (за счет массовых пикников соскучившихся граждан при наличии хорошей погоды). Две эти ситуации будут обеспечивать два пика распределения, то есть будет наблюдаться ситуация двумодальности распределения, хотя при симметричности распределения математическое ожидание может оставаться по прежнему нулевым.

Поэтому второй и основной целью исследований является выявление и описание характера и степени некорректности применения различных общепринятых методов построения доверительных интервалов для прогноза в ситуации, когда предположения постулируются, но не выполняются, проведения сравнительного анализа методов между собой, выработка рекомендаций о практической применимости метода в рассмотренных ситуациях.

Для этого в соответствии с методикой компьютерного моделирования формируем псевдо реальные значения прогнозов. Псевдо реальное значение для сезона определяется как сумма математического ожидания значения показателя (равного ), и смоделированного значения в соответствии с тем законом распределения, который указан в задании. Это делается для того, чтобы была возможность говорить о среднем числе выходе реальных значений за границы доверительного интервала на основании не одной выборки реальных значений, а при выборке объёмом N (при проведении исследований берётся N = 1000) наших псевдо реальных значений.