14)Суть мнк для построения множественного линейного уравнения регрессии.

Самым распространенным методом оценки параметров уравнения множественной линейной регрессии является ме­тод наименьших квадратов (МНК). Напомним, что его суть состоит в минимизации суммы квадратов отклонений наблю­даемых значений зависимой переменной Уj от ее значений У, получаемых по уравнению регрессии.

Для отражения того факта, что реальные значения зависи­мой переменной не всегда совпадают с ее условными математи­ческими ожиданиями и могут быть различными при одном и том же значении объясняющей переменной (наборе объясняю­щих переменных), фактическая зависимость должна быть до­полнена некоторым слагаемым, которое, по существу, являет­ся СВ и указывает на стохастическую суть зависимости. Из это­го следует, что связи между зависимой и объясняющей(ими) переменными выражаются соотношениями

(4.3)

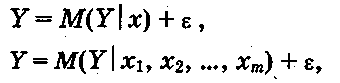
(4.4)

называемыми регрессионными моделями (уравнениями).

15)Статистическая значимость коэффициентов регрессии.

Как и в случае парной регрессии, стати­стическая значимость коэффициентов множественной линей­ной регрессии с т объясняющими переменными проверяется на основе t-статистики:

(6.33)

имеющей в данной ситуации распределение Стьюдента с числом степеней свободы = n — m— 1 (n — объем выборки). При требуе­мом уровне значимости наблюдаемое значение -статистики срав­нивается с критической точкой распределения Стьюдента.

Если , то коэффициент считается статисти­чески значимым.

В противном случае ( ) коэффициент считается статистически незначимым (статистически близким к нулю). Это означает, что фактор X_j линейно не связан с зависимой пе­ременной У. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Не оказывая сколь-нибудь серьезного влияния на зависимую переменную, он лишь искажает реальную картину взаимосвязи. Поэтому после уста­новления того факта, что коэффициент статистически незна­чим, рекомендуется исключить из уравнения регрессии пере­менную Xj. Это не приведет к существенной потере качества мо­дели, но сделает ее более конкретной.

Зачастую строгая проверка значимости коэффициентов за­меняется простым сравнительным анализом.

Если ( )то коэффициент статистически незначим.

Если то коэффициент относительно значим. В данном случае рекомендуется воспользоваться таб­лицей критических точек распределения Стьюдента (прило­жение 2).

Если 2 < 3, то коэффициент значим. Это утверждение яв­ляется гарантированным при

> 20 и > 0,05 (приложение 2).

Если , то коэффициент считается сильно значимым. Вероятность ошибки в данном случае при достаточном числе наблюдений не превосходит 0,001.

16)Интервальные оценки коэффициентов регрессии

По аналогии с парной регрессией после опре­деления точечных оценок коэффициентов - (j =0,1,…,m) теоретического уравнения регрессии могут быть рассчитаны ин­тервальные оценки указанных коэффициентов. Для построения интервальной оценки коэффициента строится -статистика

(6.26)

имеющая распределение Стюдента с числом степеней свободы v= n — т — 1 (n— объем выборки, т - количество объясняю­щих переменных в модели)

Пусть необходимо построить 100(1 — )%-й доверительный интервал для коэффициента Тогда по таблице критических точек распределения Стьюдента по требуемому уровню значи­мости а и числу степеней свободы находят критическую точку Удовлетворяющую условию

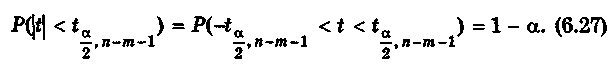
Подставляя (6.26) в (6.27), получаем

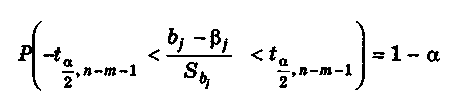
или после преобразования

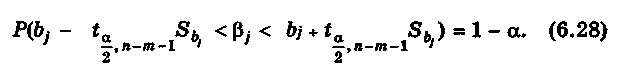
Напомним, что рассчитывается по формуле

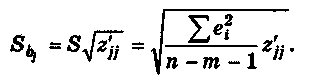
Таким образом, доверительный интервал, накрывающий с надежностью (1 – ) неизвестное значение параметра , опре­деляется неравенством

Отметим, что по аналогии с парной регрессией (может быть построена интервальная оценки для среднего значения предсказания:

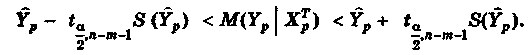
В матричной форме это неравенство имеет вид: