10)Доверительный интервал для предсказания индивидуальных значений зависимой переменной.

На практике иногда более важно знать дисперсию У, чем ее средние значения или доверительные интервалы для условных математических ожиданий. Это позволяет опреде­лить допустимые границы для конкретного значения Y.

Пусть нас интересует некоторое возможное значение y₀ переменной У при определенном значении х_р объясняющей переменной X. Предсказанное по уравнению регрессии значе­ние У при X = x_p составляет у_р. Если рассматривать значение у о как CB Y₀ , а. у₂ — как СВ Y_p, то можно отметить, что

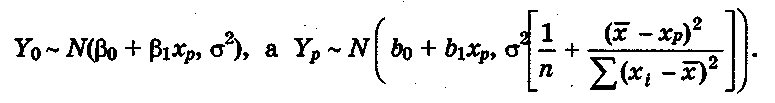
С

В и являются независимыми, а следовательно , СВ имеет нормальное распределение с

Но тогда можно показать, что

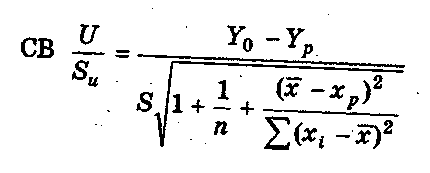
имеет нормальное распределение Стьюдента с числом степеней свободы .

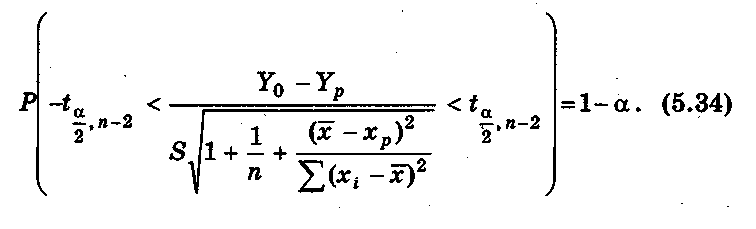
На основании этого можно сделать вывод, что интервал

определяет границы, за пределами которых могут оказаться не более 100 % точек наблюдений при X = х_р. Заметим, что данный интервал шире доверительного интервала для условного математического ожидания (на рис. 5.4 границы этого интервала отмечены пунктирной линией).

Проводя анализ построенных интервалов, несложно заме­тить, что наиболее узкими они будут при Х_р = . По мере удаления Х₀ от среднего значения доверительные интервалы расши­ряются (рис. 5.4). Поэтому необходимо достаточно осторожно экстраполировать полученные результаты на прогнозные области. С другой стороны, с ростом числа наблюдений n эти интервалы сужаются к линии регрессии при n .

11)Каким образом определяется модель множественной линейной регрессии?

модель множественной линейной регрессии.

Теоретическое линейное уравнение регрессии имеет вид:

или для индивидуальных наблюдений i, i = 1, 2,…, n,

Здесь — вектор размерности (т + 1) неиз­вестных параметров. , у = 1, 2, ..., т, называется -м теорети­ческим коэффициентом регрессии (частичным коэффициентом регрессии). Он характеризует чувствительность величины Y к изменению . Другими словами, он отражает влияние на ус­ловное математическое ожидание M( ) зависи­мой переменной У объясняющей переменной Х_j при условии, что все другие объясняющие переменные модели остаются по­стоянными. — свободный член, определяющий значение У в случае, когда все объясняющие переменные X_j) равны нулю.

После выбора линейной функции в качестве модели зависи­мости необходимо оценить параметры регрессии.

Пусть имеется n наблюдений вектора объясняющих пере­менных X = (X₁, X₂, ..., Х_т) и зависимой переменной У:

Для того чтобы однозначно можно было бы решить задачу отыскания параметров (т.е. найти некоторый наи­лучший вектор ), должно выполняться неравенство . Если это неравенство не будет выполняться, то существует бес­конечно много различных векторов параметров, при которых линейная формула связи между X и У будет абсолютно точно соответствовать имеющимся наблюдениям. При этом, если , то оценки коэффициентов вектора рассчитываются единственным образом — путем решения системы т + 1 линей­ного уравнения:

Например, для однозначного определения оценок парамет­ров уравнения регрессии достаточно иметь выборку из трех наблюдений ( ),i = 1, 2, 3. В этом случае найденные значения параметров опреде­ляют такую плоскость в трехмерном про­странстве, которая пройдет именно через имеющиеся три точ­ки. С другой стороны, добавление в выборку к имеющимся трем наблюдениям еще одного приведет к тому, что четвертая точка ( ) практически наверняка будет лежать вне построенной плоскости (и, возможно, достаточно далеко). Это потребует определенной переоценки параметров.

Таким образом, вполне логичен следующий вывод: если чис­ло наблюдений больше минимально необходимого, т.е. n > m+1, то уже нельзя подобрать линейную форму, в точности удовлетво­ряющую всем наблюдениям, и возникает необходимость опти­мизации, т.е. оценивания параметров , при которых формула дает наилучшее приближение для имеющихся на­блюдений.

В данном случае число = n — т — 1 называется числом степеней свободы. Нетрудно заметить, что если число степеней свободы невелико, то статистическая надежность оцениваемой формулы невысока. Например, вероятность верного вывода (по­лучения более точных оценок) по трем наблюдениям сущест­венно ниже, чем по тридцати. Считается, что при оценивании множественной линейной регрессии для обеспечения статисти­ческой надежности требуется, чтобы число наблюдений по крайней мере в 3 раза превосходило число оцениваемых пара­метров.

Самым распространенным методом оценки параметров уравнения множественной линейной регрессии является ме­тод наименьших квадратов (МНК). Напомним, что его суть состоит в минимизации суммы квадратов отклонений наблю­даемых значений зависимой переменной У от ее значений У, получаемых по уравнению регрессии.