31)Гетероскедастичность. Последствия гетероскедастичности.

Суть: Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений (параг­раф 5.1, предпосылка 2°): дисперсия случайных отклонений постоянна. = D( ) = для любых наблюдений i и j.

Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невы­полнимость данной предпосылки называется гетероскедастичностъю (непостоянством дисперсий отклонений).

На рис. 8.1 приведены два примера линейной регрессии — зависимости потребления С от дохода I: С = .

С С

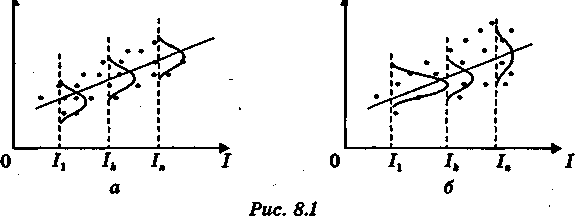
Динамика изменения дисперсий (распределений) отклонений для данного примера проил­люстрирована на рис. 8.2. При гомоскедастичности (рис. 8.2, а) дисперсии постоянны, а при гетероскедастичности (рис. 8.2, б) дисперсии изменяются (в нашем примере увеличиваются).

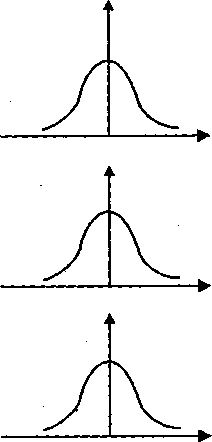Рис 8.2

Проблема гетероскедастичности характерна для перекрест­ных данных и довольно редко встречается при рассмотрении временных рядов.

Последствия: При невыполнимости данной предпосылки (при гетероске­дастичности) последствия применения МНК будут следующи­ми.

Оценки коэффициентов по-прежнему останутся несме­щенными и линейными.

3. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками дан­ного параметра). Они не будут даже асимптотически эффектив­ными. Увеличение дисперсии оценок снижает вероятность по­лучения максимально точных оценок.

4. Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что не объясненная

уравнением регрессии дисперсия (т - число объ ясняющих переменных), которая используется при вычисле­нии оценок дисперсий всех коэффициентов (формула (6.23)), не является более несмещенной.

4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным за­ иключениям по построенной модели. Вполне вероятно, что стан­дартные ошибки коэффициентов будут занижены, а следова­тельно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковы­ми на самом деле не являющихся.

Обнаружение: а) Графический анализ остатков

б) Тест ранговой корреляции Спирмена

в) Тест Парка

г) Тест Глейзера

д) Тест Голдфелда—Квандта

32)Методы смягчения гетероскедастичности

Гетероскедастичность приводит к неэффективности оценок, не смотря на их несмещенность. Так как это может обусловить необоснованные выводы по качеству модели, то при установлении возникает гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Для этого используются следующие методы смягчения гетероскедастичности:

1. Метод взвешенных наименьших квадратов. Применяется при известных для каждого наблюдения значениях 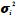. Гетероскедастичность при данном методе устраняется путем деления каждого наблюдаемого значения на соответствующее ему значение дисперсии. В этом и заключается суть метода ВНК. Таким образом, метод ВНК включает следующие этапы:

– значение каждой пары наблюдений делят на известную величину дисперсии. Тем самым наблюдениям с наименьшими дисперсиями придаются наибольшие «веса», а с максимальными дисперсиями – наименьшие «веса». Т.е., наблюдения с наименьшими дисперсиями отклонений будут более значимыми при оценке коэффициентов регрессии, чем наблюдения с большими дисперсиями. Учет этого факта увеличивает вероятность получения более точных оценок.

– по МНК для преобразованных значений строится уравнение регрессии без свободного члена с гарантированными качествами оценок.