7.6 Свойства определенных интегралов

1. Интеграл по ориентированному промежутку.

Когда вводилось понятие определенного интеграла , то неявно предполагалось, что нижний предел меньше верхнего, то есть что . А можно ли придать смысл интегралу ?

Такой смысл придается введением понятия ориентации промежутка интегрирования.

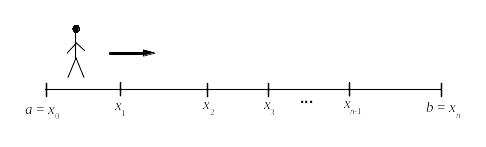
Вспомним еще раз, как строилось понятие определенного интеграла. Отрезок разбивался на кусочки, по которым строилась интегральная сумма. Представим теперь, что эти кусочки проходятся в направлении от точки а к точке b и величина определяется так: из координаты точки, которая проходится позже вычитается координата точки, которая проходится раньше то есть .

А теперь вернемся к интегралу . Что изменилось? Нижний предел стал b, а верхний  а. Это трактуют так: отрезок проходится теперь в обратном направлении, от точки b к точке а:

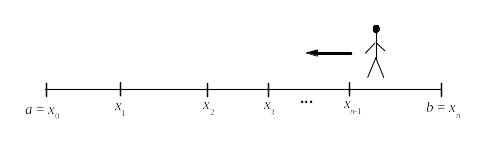
Но тогда меняются величины : они становятся равными , так как теперь точка проходится позже точки . Очевидно соотношение между этими величинами: .

Но тогда интегральные суммы в первом и втором случаях принимают вид

; ,

и, после предельного перехода , получаем соотношение

.

Таким образом, перестановка местами верхнего и нижнего пределов приводит с изменению знака интеграла.

Следствие. Рассмотрим интеграл , у которого верхний и нижний пределы одинаковы. Меняя их местами, получим

,

откуда следует, что .

2. Если , то .

Это свойство называется аддитивностью определенного интеграла относительно промежутка интегрирования.

Снова рассмотрим разбиение промежутка на кусочки так, что точка с попадает в число точек деления. Тогда относительно интегральных сумм можно написать

.

Делая предельный переход , получаем

, что и приводит к требуемому соотношению:

.

3.  .

Действительно, для интегральных сумм верно соотношение

.

После предельного перехода

получаем, что .

4.  .

Записывая соотношение для интегральных сумм

и делая предельный переход

,

получим требуемое соотношение .

5. Если , то .

Действительно, так как , то все . Поэтому

.

Делая предельный переход и учитывая непрерывность функции , получим

,

что и дает .

6. Если и , то .

Действительно, в этом случае , и, так как все , то . Суммируя и переходя к пределу

,

получим требуемое свойство .

7.7 Первая теорема о среднем

Теорема. Пусть

1. Функции и интегрируемы на ;

2. Существуют конечные m и m такие, что ;

3. .

Тогда существует число  такое, что

1.  ;

2.  .

Доказательство.

Имеем . Так как , то

.

Интегрируя это неравенство, получаем

. (*)

Возможны следующие варианты:

а) . Но тогда из (*) следует, что и  может быть взято любым.

б) . Тогда, деля все части неравенства (*) на , получим:

.

Обозначим . Тогда будет

1.  ;

2.  . 

Следствие. Если непрерывна на , то такая, что

.

Доказательство. Имеем следующую цепочку следствий:

непрерывна на  по первой теореме Вейерштрасса существуют и так что  по второй теореме БольцаноКоши такая, что для . Заменяя в первой теореме о среднем  на , получим следствие. 

Частный случай. Пусть и непрерывна на . Тогда такая, что

.

Здесь использован тот факт, что . Обоснование этого см. в следующем разделе.

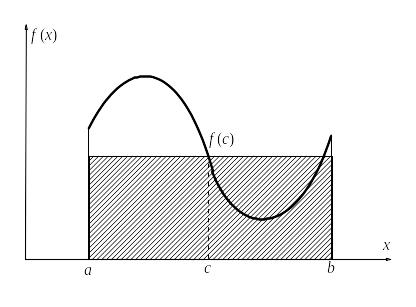
Эта формула допускает следующую геометрическую интерпретацию (см. рис.): такая, что площадь, ограниченная кривой и отрезком , лежащим на оси абсцисс, равна площади прямоугольника, с основанием в виде этого же отрезка и высотой .