Глава VII Определенный интеграл

7.1 Процедура построения определенного интеграла

Пусть нам заданы следующие объекты

1. Отрезок конечной длины .

2. Функция , которая определена и ограничена на этом отрезке.

Проведем следующее построение:

1. Разбиение отрезка на кусочки

Разобьем отрезок произвольным образом на части (кусочки) точками (см. рисунок). Для единообразия, точку а будем называть точкой х₀, а точку b  точкой х_п.

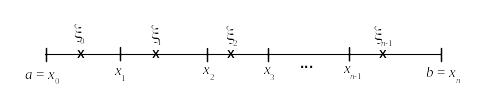
Пусть есть длина i-го кусочка и  самая большая из этих длин.

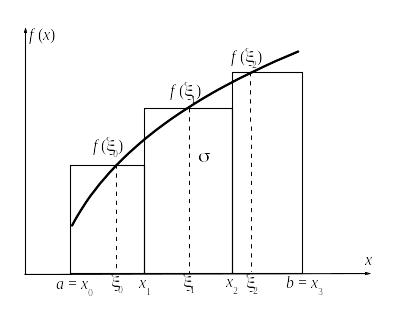
2. Составление интег8888ральной суммы

На каждом из кусочков возьмем произвольно некоторую точку (она называется средней точкой, хотя, конечно, не обязательно лежит на середине кусочка), так что и составим сумму , которая называется интегральной суммой. Геометрически она представляет собой сумму площадей прямоугольников высотой и длиной основания (см. рис.).

3. Предельный переход

Наконец, перейдем к пределу .

Определение. Если существует и не зависит от

А) способа разбиения отрезка на кусочки и от

Б) способа выбора средней точки,

то он называется определенным интегралом от функции на отрезке и обозначается символом :

= .

Функция называется подынтегральной функцией, число а (b)  верхним (нижним) пределом интегрирования.

7.2 Суммы Дарбу

Перейдем теперь к построению теории определенного интеграла. Она достаточно сложна. Ее основой являются так называемые суммы Дарбу.

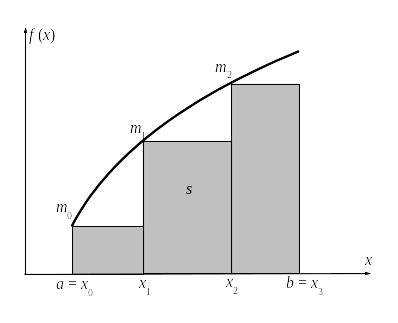
Пусть и есть наименьшее и наибольшее значения функции на i-м кусочке. Суммы и носят название нижней и верхней сумм Дарбу. Их геометрический смысл ясен из приведенных ниже рисунков.

Так как , то при любом выборе средней точки. Ясно также, что при фиксированном разбиении отрезка на кусочки и , где inf и sup берутся по всевозможным выборам средних точек.

Свойства сумм Дарбу

1. Если к имеющимся точкам деления добавить новые, то s может только увеличиться, а S  только уменьшиться.

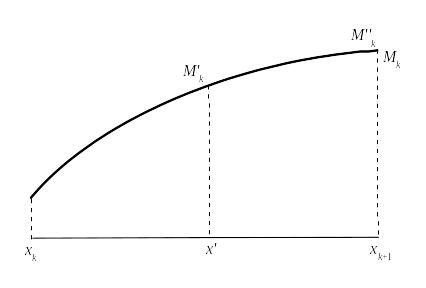
Рассмотрим кусочек и представим себе, что на нем появилась еще одна точка , так что (см. рис.).

Пусть , и . Так как и , то ясно, что и .

Рассмотрим отдельное слагаемое, скажем, верхней суммы Дарбу, соответствующее отрезку . До добавления точки оно было равно . После добавления точки оно превратилось в два слагаемых и стало равно . Так как и , то и поэтому от добавления точки верхняя сумма Дарбу не могла возрасти. Аналогично можно получить, что от добавления точки нижняя сумма Дарбу не могла уменьшиться.

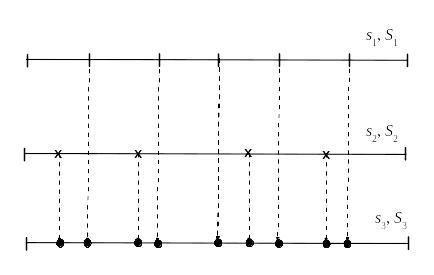
2. Каждая нижняя сумма Дарбу не превосходит любой верхней суммы Дарбу, даже если они принадлежат различным разбиениям отрезка на кусочки.

Пусть имеется два разбиения отрезка на кусочки (см. рис.)

В первом разбиении, очевидно, , во втором  . Объединим эти два разбиения в одно, смешав вместе все точки деления (см. рис.). Тогда, учитывая свойство 1, получим следующую цепочку неравенств , откуда следует, что , что и требовалось доказать.

Отсюда следует, что множество нижних сумм Дарбу , соответствующих различным разбиениям отрезка ограничено сверху любой верхней суммой Дарбу, а множество верхних сумм Дарбу ограничено снизу любой нижней суммой Дарбу. Поэтому существуют и . Они носят название нижнего и верхнего интегралов Дарбу. Очевидно, что для любого разбиения отрезка на кусочки верно соотношение .