5. Структурная схема математической модели вертикальных колебаний колесной машины с линейной подвеской и упругими шинами.

По дифференциальным уравнениям вертикального движения колёсной машины (1) и (2) составлены их структурные схемы, которые приведены на рис.3-7.

Полная структурная схема математической модели вертикальных колебаний колесной машины с линейной подвеской и упругими шинами приведена на рис.3.

Структурная схема блока многомерной модели микропрофиля дорожного покрытия, построенная с использованием матричных блоков библиотеки Simulink, приведена на рис. 2. Структура схемы на рис.2 соответствует уравнению передаточной функции (7). Схема отличается использованием матричных усилителей Matrix Gain, которые имеют значения коэффициентов усиления в форме матриц.

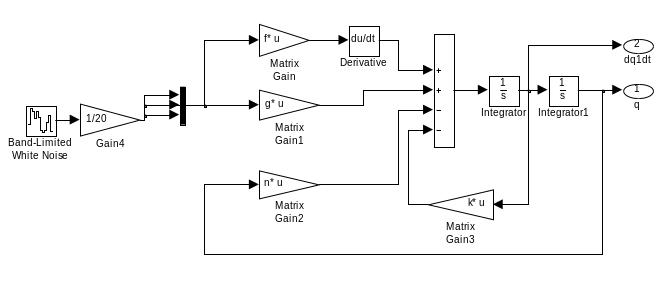
Рис. 2.- Структурная схема блока модели микропрофиля дорожного покрытия построенная с использованием матричных блоков (прикладная программа Simulink)

Структурная схема линейной модели шины колеса (прикладная программа Simulink, блок SHINA на рис.3) отражена на рис. 4.

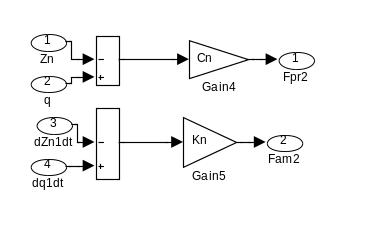
Рис.4 - Структурная схема линейной модели шины колеса (прикладная программа Simulink, блок SHINA на рис.3)

Структурная схема линейной модели подвески автомобиля (прикладная программа Simulink, блок Podveska на рис.3) отражена на рис.5.

Структурная схема модели динамики вертикальных колебаний неподрессоренной массы автомобиля (прикладная программа Simulink, блок MOST на рис.3) отражена на рис.6.

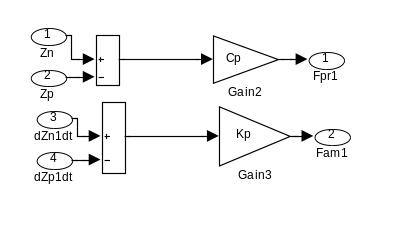
Рис.5 - Структурная схема линейной модели подвески автомобиля (прикладная программа Simulink, блок Podveska на рис.3)

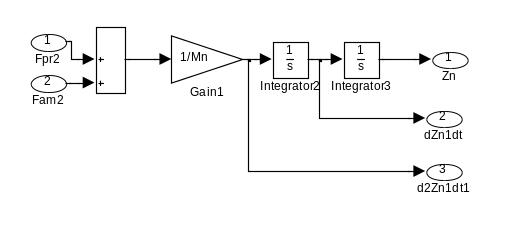
Рис.6 - Структурная схема модели вертикальных колебаний неподрессоренной массы автомобиля (прикладная программа Simulink, блок MOST на рис.3)

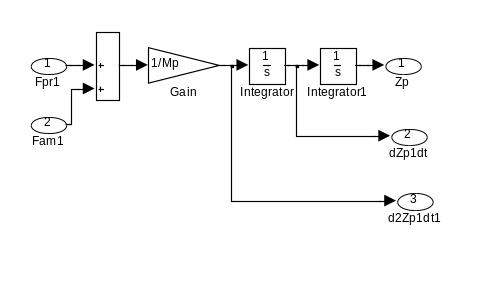
Рис.7 - Структурная схема модели вертикальных колебаний подрессоренной массы автомобиля (прикладная программа Simulink, блок KUZOV на рис.3)

Структурная схема модели вертикальных колебаний подрессоренной массы автомобиля (прикладная программа Simulink, блок KUZOV на рис.3) отражена на рис.7.

6. Исследование математической модели вертикальных колебаний колесной машины с линейной подвеской и упругими шинами

По разработанным математическим моделям рассматриваемых микропрофилей дорог выполнено моделирование в среде Simulink (Matlab).

Интегрирование дифференциальных уравнений моделей микропофилей осуществлялось численным методом вычислительной математики методом Рунге-Кутта четвёртого порядка в интервале времени t = 0…10с. Результаты интегрирования моделей микропрофелей трёх дорог приведены на рис.8 в форме графиков, отражающих изменения вертикальных перемещений q точки контакта колеса во времени.

Рис. 8 – Моделируемые вертикальные перемещения во времени t точки контакта колеса q для микропрофилей трёх дорожных покрытий

Исследование объединённой математической модели вертикальных колебаний колёсной машины, содержащей динамические математические модели микропрофилей дорог и модель вертикальных перемещений масс машины, структурная схема которой приведена на рис.3, проводилось с использованием численного метода интегрирования Рунге-Кутта программы Simulink.

Результаты интегрирования математической модели вертикальных колебаний колёсной машины приведены на рис.9 в форме графиков, отражающих моделируемые колебания во времени t вертикальных перемещений Z_p подрессоренной массы от воздействия изменения высот q микропрофилей трёх дорог.

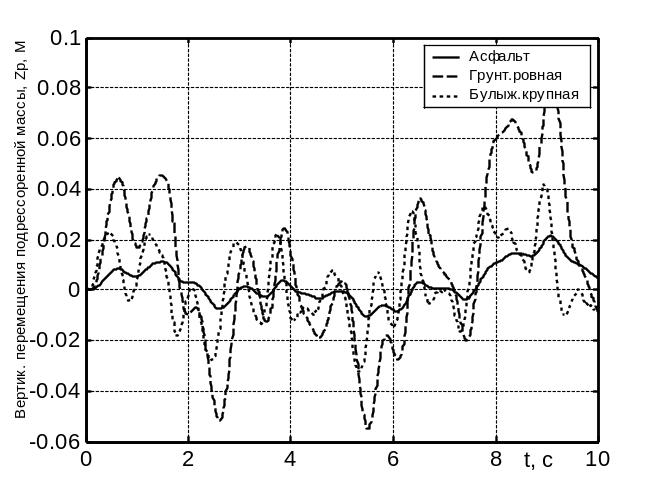
Рис.9 Моделируемые колебания во времени t вертикальных перемещений Z_p подрессоренной массы от воздействия изменения высоты q микропрофилей трёх дорог

Исследование программы объединённой модели показало возможность лёгкого вывода на экран монитора следующих графиков: вертикальных перемещений подрессоренной и неподрессоренной масс их скоростей и ускорений по времени. Кроме графиков рис.9 графики других переменных состояния колёсной машины, определяющие плавность хода, не приводятся в настоящей работе.

Результаты моделирования колебаний вертикального перемещения Z_p подрессоренной массы под воздействием скачкообразного изменения высоты q дороги приведены графиками переходного процесса во времени t на рис.10.

Анализ графика колебаний вертикальных перемещений подрессоренной массы показывает, что колебания затухающие имеют сложный характер, отличающийся наложением на низкочастотные затухающие колебания большой амплитуды затухающих колебаний высокой частоты и малой амплитуды

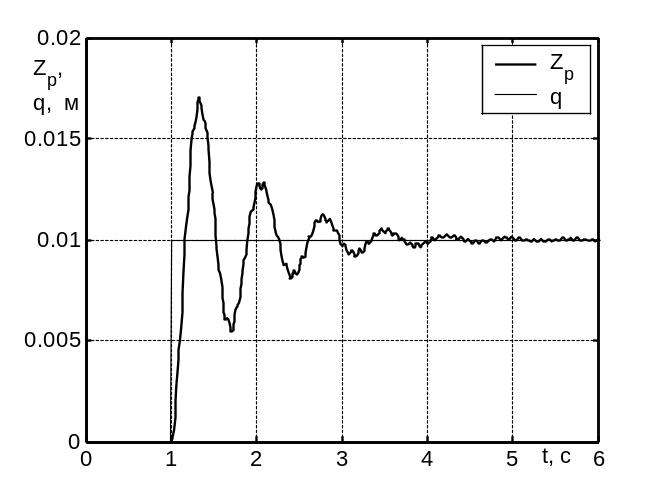
Рис.10 – Моделируемые колебания во времени t вертикального перемещения Z_p подрессоренной массы под воздействием скачкообразного изменения высоты q дороги