§ 13.3. Примеры использования квантовых статистик.

­1. В полости объема V при Т=const в состоянии термодинамического равновесия со стенками находится излучение абсолютно-чёрного тела. Поскольку для фотонов спин равен , его можно рассматривать как фотонный газ, подчиняющийся статистике Бозе-Эйнштейна . Для фотонов m = О и распределение Бозе-Эйнштейна имеет вид:

¦_Б-Э= . (13.22)

Это объясняется непостоянством числа фотонов в полости и их зависимостью от температуры. Равновесность излучения достигается за счет излучения и поглощения стенками полости.

Запишем функцию распределения Планка для излучения абсолютно черного тела:

_П(l,T)= . (13.23)

Следовательно, распределение Планка вытекает из распределения Бозе-Эйнштейна.

Запишем функцию распределения Вина:

_В(l,T)= . (13.24)

Cледовательно функция Вина вытекает из распределения Максвелла-Больцмана.

2 . Анализ распределения Ф-Д для электронного газа при Т=0 К. Пусть при Т=0 К m=m_о. Если Т® 0, W< m_o, то¦_Ф-Д =1; если Т® 0, W > m_o, то _¦Ф-Д =0. Смысл этого результата: при Т=0 К все энергетические состояния равномерно заполнены по одному электрону в каждом состоянии вплоть до энергии W_F =m_o, которая называется энергией Ферми и представляет собой максимальную энергию, которую могут иметь электроны в металле при Т=0 К (рис. 13.6).

f_Ф-Д=

(13.25)

Распределение Ферми-Дирака нечувствительно к изменению температуры. Функция _¦Ф-Д (W) искажается в интервале 2kT, так что _¦Ф-Д(m)=1/2 (рис.13.7).

З ависимость химического потенциала m от температуры имеет вид:

(13.26)

W_F>>kT, поэтому m(T) @W_F, A @ exp >>1 - электронный газ в металле всегда вырожден.

С помощью распределения Ферми-Дирака можно объяснить вопросы, связанные с распределением импульсов, скоростей, энергии электронов, теплоёмкости электронного газа, сверхпроводимости металлов.

Внутренняя энергия моля электронного газа:

. (13.27)

Чтобы оценить результаты, даваемые квантовой статистикой, сравним их с классической электронной теорией. Её основными законами являются законы Ома и Джоуля-Ленца в дифференциальной форме:

, (13.28)

, (13.29) где удельное сопротивление:

. (13.30) Здесь <l> - средняя длина свободного пробега электронов,

<u> - средняя арифметическая скорость теплового движения.

Основными недостатками электронной теории являются невозможность объяснить:

- экспериментально наблюдаемую в широком интервале температур линейную зависимость между удельным сопротивлением r и абсолютной температурой

r_экс ~ T. (13.31)

Поскольку <u> ~ T^1/2, то

r_экс ~ T^1/2. (13.32)

- значение молярной теплоёмкости металлов.

Согласно экспериментальному закону Дюлонга и Пти:

С_{М мет.Экс.} @ С_{М тв.м. @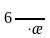} @ . (13.33)

В соответствии с классической теорией:

С_{М мет.теор. @} =С_{М ион.кр.реш.} + С_{м Эл.газа} = = + @ + = , (13.34) т.е. электронная составляющая теплоёмкости металлов как бы отсутствует.

В соответствии с квантовой теорией электропроводности металлов удельная электропроводность определяется соотношением:

, (13.35)

где <l_F> - средняя длина свободного пробега электрона, имеющего энергию Ферми;

u_F - скорость теплового движения такого электрона.

, (13.36) где Е - модуль упругости Юнга;

d - период кристаллической решётки.

Подставляя (13.36) в (13.31), получим:

r _теор.= Т~Т. (13.37)

Для Ag r _теор ~5·10⁷ Ом^-1м^-1, r _экс ~6·10⁷ Ом^-1м^-1. При очень низких температурах формула (13.37) не справедлива. В этом случае <l_F>~1/T⁵ и r _{теор ~}Т⁵.

Молярная теплоёмкость электронного газа

С_{М Эг.кв.} = = . (13.38)

Классическая физика даёт результат:

С_{М Эг.кв.} = . (13.39)

Отсюда

. (13.40)

Для комнатных температур kT/W_F ~ 0,01, поэтому

~0,03, (13.41) т.е. теплоёмкость электронного газа ничтожно мала. Это связано с тем, что в процессе изменения внутренней энергии электронного газа при нагревании участвует незначительное число электронов, находящихся в области спада функции распределения f_Ф-Д.

Приложения. Дополнительные разделы квантовой механики.