
- •Кафедра физики
- •Элементы атомной, ядерной и статистической физики
- •Одесса – 2007
- •Формулы Эйлера:
- •Производные некоторых функций
- •Интегралы от некоторых функций
- •Международная система единиц Основные единицы
- •Дополнительные единицы
- •Производные единицы
- •Примеры
- •Элементы физики атомного ядра и элементарных частиц
- •I.I. Классификация физических процессов и явлений
- •1.2. Единицы физических величин
- •2. Заряд атомного ядра. Зарядовое и массовое числа. Момент импульса ядра и его магнитный момент.
- •3. Дефект массы и энергия связи ядра
- •4. Закономерности и происхождение a -, b - и g - излучения атомных
- •4.1. Явление радиоактивности
- •4.2. Закон радиоактивного распада
- •4.3. Закон смещения к.Фаянса – ф.Содди
- •4.4. Радиоактивные семейства. Активность радионуклида
- •1МэВ Wmax
- •Основные понятия дозиметрии ионизирующих излучений.
- •5. Ядерные реакции
- •6. Реакция деления ядра. Цепная реакция деления. Понятие о ядерной энергетике.
- •6. Реакция синтеза атомных ядер. Проблема управляемых термоядерных реакций.
- •8. Элементарные частицы. Их классификация и взаимная превращаемость. Основные типы взаимодействий.
- •8.1. Понятие элементарных частиц.
- •8.2. “Зоопарк” элементарных частиц. Типы взаимодействий.
- •8.3. Полуфеноменологическая систематика частиц.
- •8.4. Законы сохранения в физике.
- •8.5. Классификация частиц. Фундаментальные частицы.
- •8.6. Модель кварков
- •8.7. Нейтрино
- •8.8. Значение физики элементарных частиц.
- •Глава 13. Элементы статистической физики.
- •§ 13.1. Классическая статистика Максвелла-Больцмана.
- •§ 13.2. Квантовые статистики Бозе-Эйнштейна и Ферми-Дирака.
- •§ 13.3. Примеры использования квантовых статистик.
- •Дополнительность и причинность в квантовой механике. Основное уравнение в квантовой механике.
- •Причина
- •Закон причинности
- •Причина
- •Закон причинности
- •Физический смысл и нормировка волновой функции.
- •Заключение
- •Рекомендованная литература
Глава 13. Элементы статистической физики.
Введение
Физические теории кажутся ясными и простыми только при поверхностном их рассмотрении. Любое углубление убеждает в их невероятной сложности. В значительной степени это касается теорий, в названии которых присутствует термин квантовая: квантовая механика, квантовая статистика, квантовая акустика, квантовая электродинамика и т. д. Тем не менее, их основные положения можно не только понять, но и успешно использовать в практической и инженерной деятельности.
Напомним: в механике движение тела однозначно определяется заданными начальными условиями и силами, действующими на тело. В этом случае можно вычислить положение тела в любой момент времени, определить результат его взаимодействия с другими телами, рассчитать, например, траектории движения планет, космических кораблей и т. п. Такие явления описываются динамическими характеристиками.
В молекулярной физике рассматриваются явления, в которых участвуют колоссальные количества молекул (в 1 см3 газа при нормальных условиях содержится » 3×1019 молекул). Движение каждой частицы обусловлено различными причинами и подчиняется законам механики, но благодаря огромному числу соударений с другими молекулами и стенками сосуда, скорость и направление движения молекулы за короткий промежуток времени претерпевает столько изменений, что практически не зависят от начальных условий движения.
Это означает, что статистические закономерности, в отличие от динамических, не определяются начальными условиями. Наблюдение за отдельными частицами невозможно - можно наблюдать лишь результат их совокупного действия. Так, например, давление газа на стенки сосуда определяется изменением суммарного импульса молекул, ударяющихся о его стенки.
Статистическая физика изучает свойства макроскопических тел, т.е. систем, состоящих из очень большого числа частиц (молекул, атомов, электронов и т. п.), исходя из свойств этих частиц и взаимодействий между ними. Большое число частиц в макроскопических телах приводит к появлению новых статистических закономерностей в поведении таких тел, в широких пределах не зависящих от конкретных условий, например, от значений начальных координат и скоростей частиц. Для статистической физики характерно вычисление не точных значений физических величин, характеризующих поведение объекта, а их средних значений.
§ 13.1. Классическая статистика Максвелла-Больцмана.
Объекты, подчиняющиеся законам классической физики, описываются статистикой Максвелла-Больцмана. При этом предполагается, что они различимы, т.е. могут быть классифицированы по какому-либо признаку или параметру, например, по скорости, кинетической, потенциальной, полной энергии.



 аспределение
Максвелла определяет распределение
молекул по скоростям (или импульсам),
т. е. распределение по кинетическим
энергиям при отсутствии внешнего
силового поля. Оно было получено
теоретически Дж. Максвеллом в 1859 г. и
подтверждено экспериментально О.Штерном
в 1920 г. Его можно представить графически
(рис. 13.1) и аналитически следующим
образом:
аспределение
Максвелла определяет распределение
молекул по скоростям (или импульсам),
т. е. распределение по кинетическим
энергиям при отсутствии внешнего
силового поля. Оно было получено
теоретически Дж. Максвеллом в 1859 г. и
подтверждено экспериментально О.Штерном
в 1920 г. Его можно представить графически
(рис. 13.1) и аналитически следующим
образом:
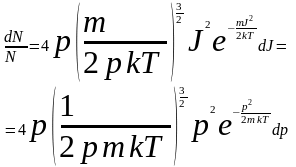 (13.1)
(13.1)
При этом заштрихованная площадь определяет долю молекул dN из общего числа N, имеющих скорости в интервале J ,J + dJ, иначе говоря вероятность того, что скорость молекул лежит в указанном интервале или импульс в интервале p, p + dp независимо от направления импульсов:
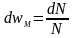 (13.2)
(13.2)
Можно также поставить вопрос о числе молекул, скорости или импульсы которых лежат в данном интервале скоростей и импульсов, задаваемых, соответственно, векторами
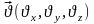 ,
,
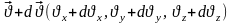 или
или
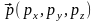 ,
,
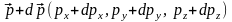 .
.
От выражения (1) можно перейти к иной форме распределения Максвелла:
 .
(13.3)
.
(13.3)
Учитывая,
что
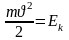 ,
а
,
а
 перепишем (13.3) в виде:
перепишем (13.3) в виде:
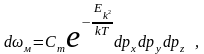 (13.4)
(13.4)
где
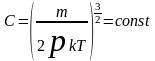 (13.5)
(13.5)
Распределение Максвелла в форме (13.4) определяет вероятность того, что проекции импульсов молекул на координатные оси лежат в интервалах от px до px+ dpx, от py до py+ dpy, от pz до pz+ dpz.



Поскольку молекулы движутся хаотически, расположение р-точек относительно начала координат оказывается сферически симметричным. Поэтому плотность р-точек (их число в единице объёма р-пространства) является функцией расстояния от начала координат, т.е. функцией модуля импульса р. Импульсы, численные значения которых ограничены интервалом dp, можно изобразить векторами, концы которых лежат внутри шарового слоя “объёмом” 4pp2dp. Импульсы, составляющие которых px, py, pz ограничены данными интервалами dpx, dpy, dpz изображаются векторами, концы которых лежат в объёме dpx dpy dpz. При указанных предположениях
4pp2dp = dpx dpy dpz . (13.6)
Если газ или другая система частиц находится во внешнем потенциальном силовом поле, например в гравитационном, то распределение частиц по высоте (по объёму) описывается распределением Больцмана. С помощью барометрической формулы Лапласа и уравнения состояния идеального газа Менделеева-Клапейрона легко получить распределение молекул в поле силы тяжести для изотермического случая:
 , (13.7)
, (13.7)







 де
n
и no
концентрации частиц соответственно на
высотах h
и ho
над поверхностью Земли (рис. 13.3 а, 13.3 б).
де
n
и no
концентрации частиц соответственно на
высотах h
и ho
над поверхностью Земли (рис. 13.3 а, 13.3 б).
h
<<
R,
ho<<
R,
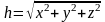 ,
,
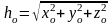 .
.
Перепишем
выражение (13.7) иначе, учитывая, что
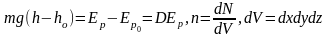 :
:
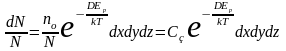 ,
(13.8)
,
(13.8)
где
 .
(13.9)
.
(13.9)
Соотношение
(13.8) определяет вероятность dwБ
того, что координаты частицы находятся
в интервалах от x
до
x+dx,
от y
до y+dy,
от z
до z+dz,
иначе говоря частица лежит в объёме
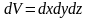 :
:
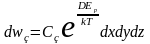 . (13.10)
. (13.10)
Поскольку распределение по скоростям и по координатам являются событиями независимыми, то суммарное распределение можно определить по теореме умножения вероятностей:
 (13.11)
где СМ-Б
= СМ
×
СБ
= сonst, W -
полная энергия частицы,
(13.11)
где СМ-Б
= СМ
×
СБ
= сonst, W -
полная энергия частицы,
 -
элемент абстрактного шестимерного
m-пространства
координат импульсов (элемент так
называемого фазового объёма).
-
элемент абстрактного шестимерного
m-пространства
координат импульсов (элемент так
называемого фазового объёма).
Выражение (13.11) можно записать иначе:
 .
(13.12)
.
(13.12)
Его можно трактовать как среднее число частиц в единице фазового объёма (в фазовой ячейке или в состоянии с энергией W. Функция fМ-Б(W) называется функцией распределения Максвелла-Больцмана.
