4. Свойства определенного интеграла

Если функция f(x) интегрируема на отрезке [a, b], то ее интеграл является числом, не зависящим от выбора обозначения для аргумента подынтегральной функции, т.е. от обозначения переменной интегрирования:

Для любой функции f(x), определенной в точке a, положим по определению .

Кроме того, для функции f(x), интегрируемой на [a, b], будем считать по определению, что .

Приведем без доказательства основные свойства определенного интеграла.

Свойство 1 (свойство линейности)

Если функции f(x) и g(x) интегрируемы на отрезке [а, b], то для любых вещественных чисел α и β справедливо равенство:

Свойство 2 (свойство адаптивности)

Если функция f(x) интегрируема на отрезках [a, b] и [с, d], то она интегрируема и на отрезке [a, d]. Причем

Свойство 3 (основная теорема интегрального исчисления)

Если функция f(x), непрерывна на отрезке [а, b] и F(x)- какая-нибудь первообразная для f(x) на эом отрезке. то справедлива формула Ньютона-Ленбница

(1)

(без доказательства).

Заметим, что такое название формулы (1) условно, т.к. ни у Ньютона, ни у Лейбница такой формулы в точном смысле этого слова. Но важно, что именно Ньютон и Лейбниц впервые установили связь между ингегрированием и дифференцированием, позволяющую создать правило для вычислениея определенных интегралов.

Символ называется знаком двойной подстановки. С его помощью формула (1) записывается так:

Пример 1. Вычислить следующие определенные интегралы по формуле (1):

5. Замена переменной и интегрирование по частям в определенном интеграле

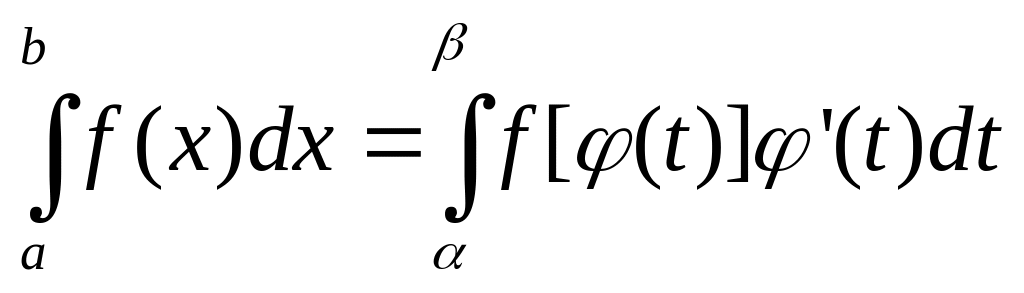Теорема 6.1 Пусть функция непрерывна на отрезке , а функция определена и непрерывна вместе со своей производной на отрезке , причем для любого и . Тогда (1)

(без доказательства)

Формула (1) называется формулой замены переменной в определенном интеграле или формулой интегрирования подстановкой.

Пример 1. Вычислить определенный интеграл .

С делаем замену переменной и пересчитаем пределы интегрирования :

Замечание. При вычислении определенного интеграла по формуле (1) мы не возвращаемся к старой переменной.

Теорема 6.2 Если функция и дифференцируемы на отрезке , то справедлива следующая формула интегрирования по частям :

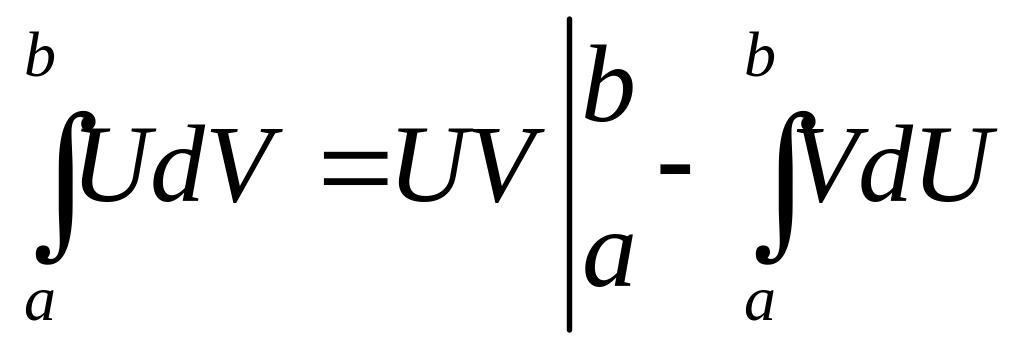(2)

(без доказательства)

Пример 2. Вычислить .

Будем брать интеграл по частям, обозначим

Тогда

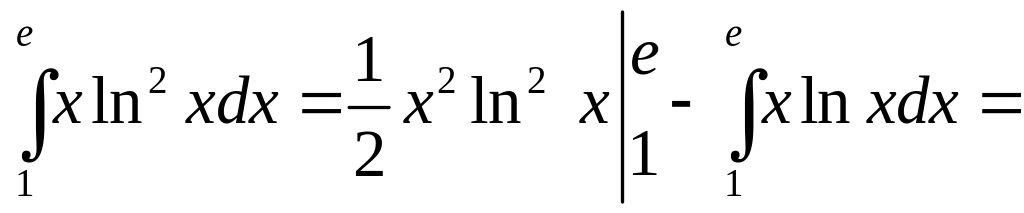
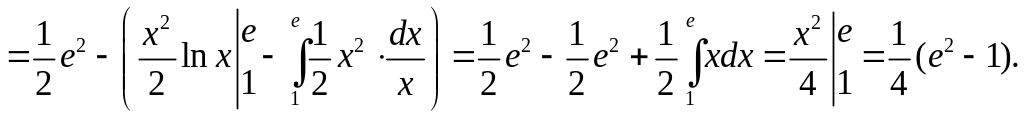
6. Геометрические приложения определенного интеграла

1) Площадь плоской фигуры

Рассмотрим функцию , непрерывную и неотрицательную на отрезке . Как уже отмечалось, криволинейная трапеция – это фигура, ограниченная графиком линии , осью и прямыми , (рис.2).

Площадь это трапеции равна

(1)

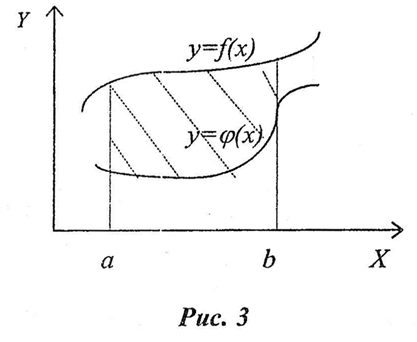
Если плоская фигура ограничена двумя непрерывными на отрезке функциями и и прямыми , (рис.3), то ее площадь вычисляется по формуле :

(2)

Пример 1. Найти площадь фигуры, ограниченной линиями и .

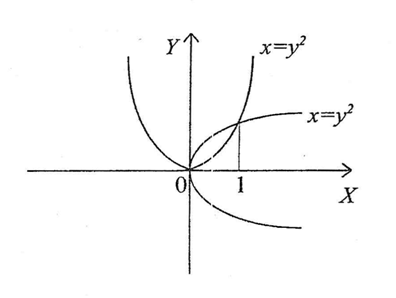
Кривые и симметричны относительно биссектрисы первого координатного угла. Точки пересечения данных кривых находим из системы уравнений

.

Применяя формулу (2), находим искомую площадь