4). Интегрирование подстановкой (замена переменной)

(3)

причем непосредственно подобрать первообразную для функции f(x) мы не можем, но нам известно, что она существует.

Сделаем замену переменной в подынтегральном выражении

(4)

Будем считать, что функция φ(t) определена и дифференцируема на некотором множестве Т, тогда

Обозначим X - множество значении функции . Если функция f(x) определена на множестве X, то вычисление интеграла (3) с помощью замены переменного (4) сводится к вычислению интеграла

(5)

который может оказаться в каком-то смысле «проще», чем исходный.

Формула (5) называется формулой интегрирования заменой переменной. Она приводится без доказательства.

Так интегралы вида

,

где R - рациональная функция, с помощью подстановки

приводятся к интегралу от рациональной функции.

Пример 1. Интеграл вычисляется с помощью подстановки . В этом случае имеем .

Отсюда .

Заметим, что (последнее равенство не трудно проверить, приведя дроби к общему знаменателю). Наш интеграл равен разности двух интегралов:

.

Теперь возвращаемся к старым переменным .

При нахождении интегралов вида , где n и m - целые числа, возможны следующие случаи:

1).Одно из чисел n или m - нечетное, например m=2k+1. Тогда

.

После замены переменной t=sin t получаем интегралы от степенной функции:

.

2). Оба числа n и m - четные. Тогда рекомендуется воспользоваться тригонометрическими формулами понижения степени:

где α - любое вещественное число.

Пример 2. Вычислить интеграл .

Преобразуем этот интеграл

5). Интегрирование некоторых иррациональных функций

Рассмотрим интеграл вида

(6)

где R - рациональная функция, а, b - постоянные, τ, s - целые положительные числа.

Обозначим m - наименьшее общее кратное чисел s₁,…,s_k с помощью подстановки

ах+b=t^m интеграл (6) приводится к интегралу от рациональной функции новой переменной t.

Пример З. Сделаем в интеграле замену переменной .

Получаем , и наш интеграл преобразуется следующим образом:

В интегралах вида можно избавиться от иррациональности ответственно подстановками .

Пример 4. В интеграле рационально сделать замену переменной , тогда

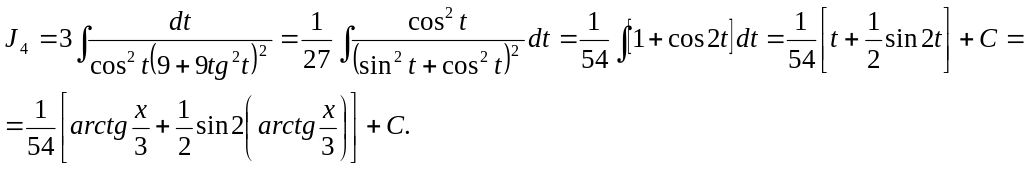
Пример5. Вычислить интеграл .

Сделаем замену переменной ,

Тогда

Этот ответ можно еще преобразовать. Так как

то окончательно имеем

Наряду с указанными подстановками можно использовать и другие.

Пример 6. Интеграл

Вычисляется с помощью подстановки .

В этом случае

3. Определенный интеграл. Его определение и геометрический смысл

Пусть на отрезке [a, b] определена некоторая функция f(x). Будем говорить, что задано разбиение отрезка [a, b], если заданы точки x₀, x₁,…,x_n, такие, что a=x₀,<x₁<…x_n-1<x_n=b.

Разбиение отрезка [a, b], будем обозначать символом {x_k}. Отрезки [xk-1, xk], k=1,…,n, называются частичными отрезками. Обозначим длины этих отрезков символами Δx_k:

Диаметром разбиения называется число .

На каждом частичном отрезке выберем произвольным образом точку и вычислим значение функции в этой точке f(ξ_k).

По данному разбиению {x_k} построим сумму

(1)

которая начинается интегральной суммой или суммой Римана.

(Георг Фридерик Бернгард Риман – немецкий математик (1826-1866). За свою короткую жизнь он опубликовал сравнительно небольшое число работ, но каждая из них была и остается важной, а некоторые из них раскрыли совершенно новые и плодотворные области).

Определение 3.1

Функция f(x), называется интегрируемой по Риману на отрезке [а, b], если для любого разбиения {x_k} у которого , и для любого выбора, точка ξ_k существует предел последовательности интегральных сумм δ_n(x_k, ξ_k), и он равен А: .

В этом случае число А называется римановым определенным интегралом функции f(x) на отрезке [а, b] и обозначается .

Это классическое определение интеграла, данное О. Коши и развитое Б. Риманом.

Рассмотрим геометрический смысл интегральной суммы в случае непрерывной неотрицательной функции .

Криволинейной трапецией назовем фигуру, ограниченную графиком функции y=f(x), прямыми x=a и x=b и отрезком [a,b] оси ОХ (рис. 1).

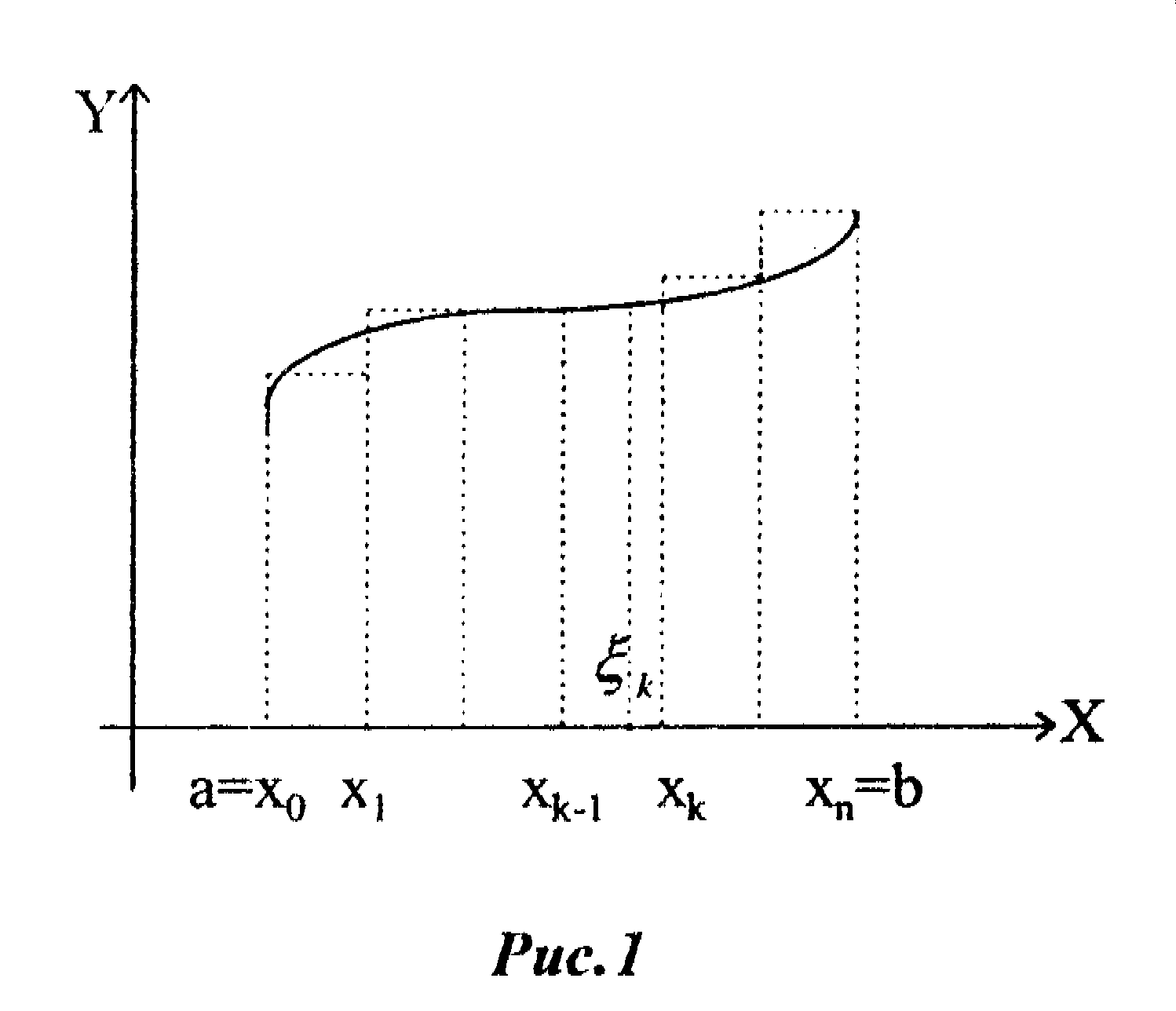
Сделаем разбиение {x_k} отрезка [а, b] и в каждом частичном отрезке [x_k-1,x_k] выберем точку ξ_k. Тогда каждое слагаемое интегральной суммы (1) равно площади прямоугольника с основанием длины Δx_k и высотой f(ξ_k). Вся же сумма δ_n(x_k, ξ_k) равна площади «ступенчатой фигуры», получающейся объединением всех указанных прямоугольников.

Из определения 3.1 следует, что определенный интеграл является пределом, при , последовательности площадей соответствующих ступенчатых фигур, поэтому он равен площади криволинейной трапеции.

Теорема. Если функция у=f(x) непрерывна на отрезке [а, b], то она интегрируема на [а, b], т.е. предел интегральной суммы (1) существует и не зависит от способа разбиения отрезка [а, b] на частичные отрезки [x_k-1, x_k] и выбора наших точек ξ_k.