
- •Методические указания к выполнению контрольной работы №1
- •Контрольная работа №1
- •Методические указания к выполнению контрольной работы №2
- •Раздел II. Дифференциальное исчисление
- •1). Производная сложной функции
- •2). Логарифмическая производная
- •3). Производная неявной функции
- •3Адание 3. Производная функции по направлению
- •Контрольная работа № 2
- •Методические указания к выполнению контрольной работы №3
- •Раздел III. Интегральное исчисление
- •1. Первообразная, неопределенный интеграл и их свойства
- •Свойства неопределенного интеграла
- •2. Основные методы интегрирования
- •1). Интегрирование путем подведения под знак дифференциала
- •2). Интегрирование по частям
- •3). Интегрирование рациональных функций
- •4). Интегрирование подстановкой (замена переменной)
- •5). Интегрирование некоторых иррациональных функций
- •3. Определенный интеграл. Его определение и геометрический смысл
- •4. Свойства определенного интеграла
- •5. Замена переменной и интегрирование по частям в определенном интеграле
- •6. Геометрические приложения определенного интеграла
- •1) Площадь плоской фигуры
- •2.Объем тела вращения
- •3) Длина дуги кривой
- •Основные понятия
- •1.2 Свойства сходящихся рядов
- •1.3 Признаки сходимости положительных рядов
- •1.4 Исследование сходимости знакопеременных и знакочередующихся рядов
- •Дифференциальные уравнения
- •Контрольная работа № 3
3Адание 3. Производная функции по направлению
Производная
функции
![]() по направлению
по направлению
![]() называется предел отношения приращения
функции при переходе от точки
называется предел отношения приращения
функции при переходе от точки
![]() к точке
к точке
![]() при условии, что
при условии, что
![]() ,
к
,
к
![]() ,
если этот предел существует и конечен,
то есть
,
если этот предел существует и конечен,
то есть
![]()
Градиентом
функции
в точке
называется
вектор

Связь
между градиентом функции
в точке
и производной этой функции в точке
в направлении
:
![]()
где
![]() - угол между градиентом и направлением
.
- угол между градиентом и направлением
.
Пример.
Найти
производную функции
![]() в точке
в точке
![]() в направлении, составляющем угол
в направлении, составляющем угол
![]() с градиентом функции
с градиентом функции
![]() в этой точке.
в этой точке.
![]()
![]()


![]()
![]()
Тогда

Задание 4. Экстремум функции двух переменных
Необходимый признак экстремума. Если функция z=f(x,y) дифференцируема при x=x0 и y=y0 достигает в ней экстремума, то в этой точке равны нулю ее частные производные:
![]()
Достаточное условие экстремума. Пусть точка М0(x0,y0) является стационарной точкой функции z=f(x,y). Вычислим в этой точке значения вторых частных производных функции f(x,y) и обозначим их для краткости буквами А, В, С:
![]()
Если В2-AC<0, то функция f(x,y) имеет в точке М0(x0,y0) экстремум: максимум при А<0 (и С<0) и минимум при А>0 (и С>0).
Если В2-AC<0, то точка М0(x0,y0) не является точкой экстремума.
Если В2-AC=0, то никакого заключения о характере стационарной точке сделать нельзя и требуется дополнительное исследование.
Пример.
Найти экстремум функции
![]()
![]()
![]()
![]()
M(21,20) – стационарная точка
Найдем значения вторых производных в точке М:
![]()
![]()
т.к. А<0, то в точке М(21,20) функция имеет максимум Zmax=482.
Контрольная работа № 2
Найти производные следующих функций:
a).
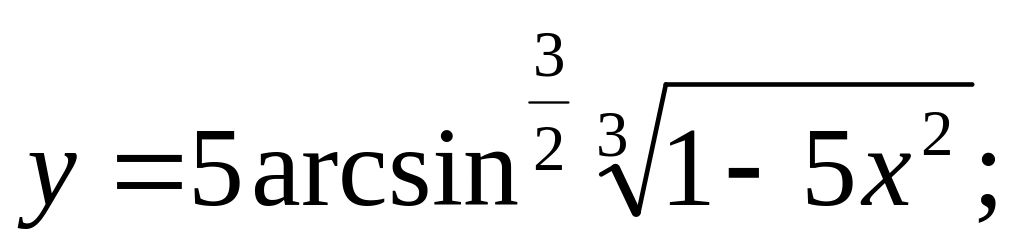 b).
b).
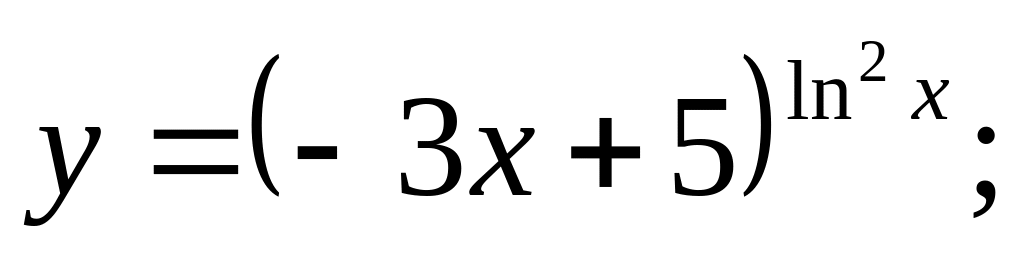 c).
c).
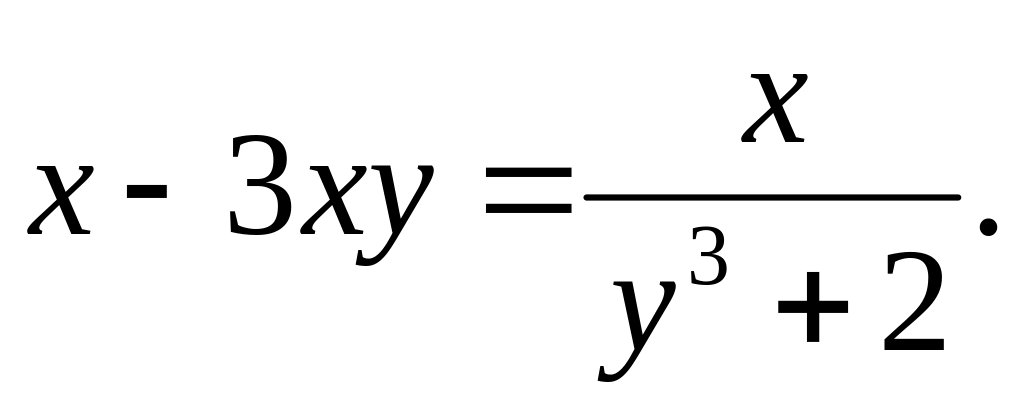
a).
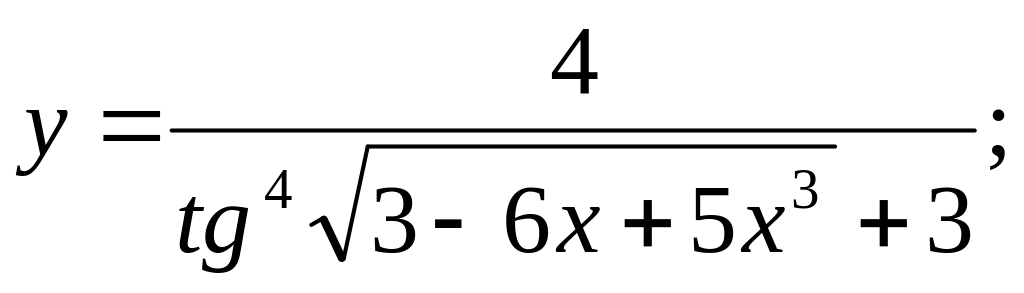 b).
b).
 c).
c).

a).
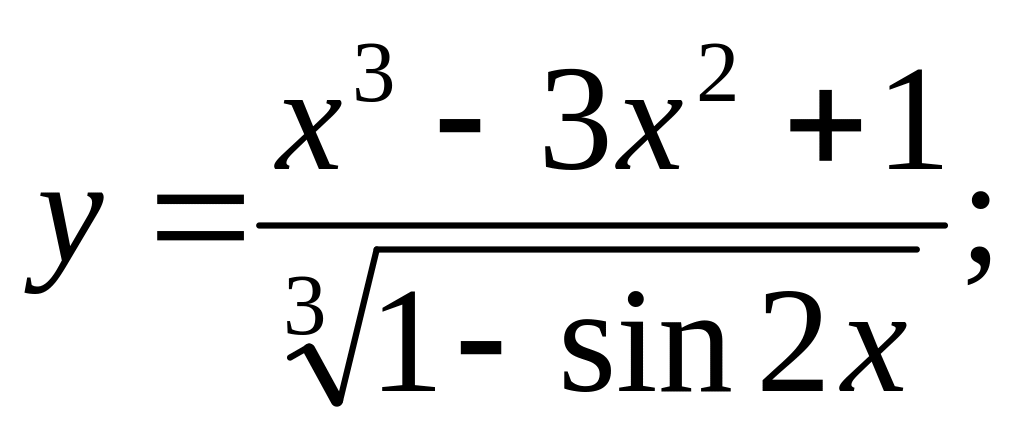 b).
b).
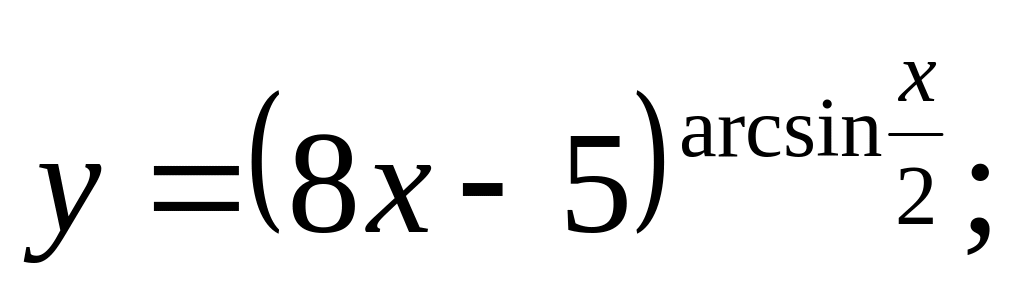 c).
c).
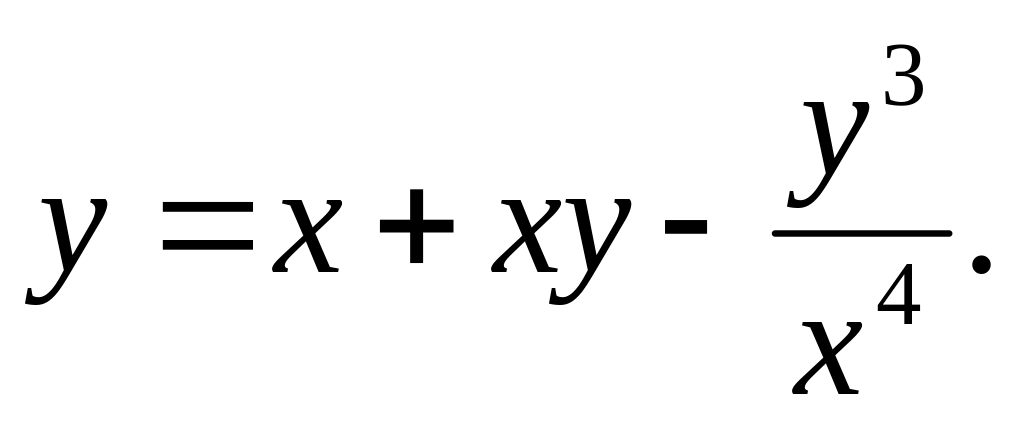
a).
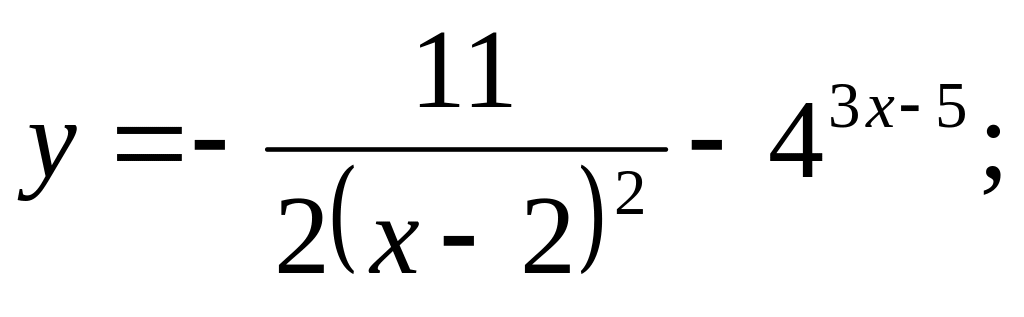 b).
b).
 c).
c).

a).
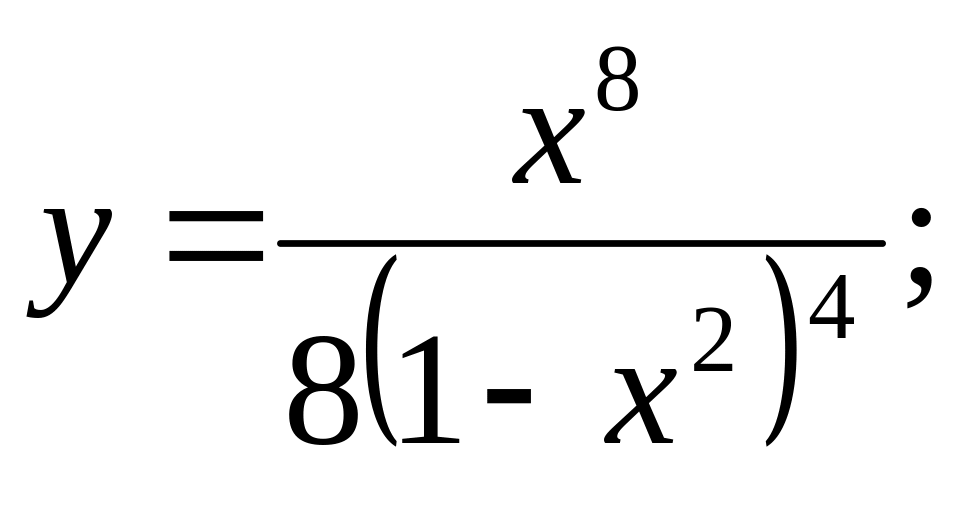 b).
b).
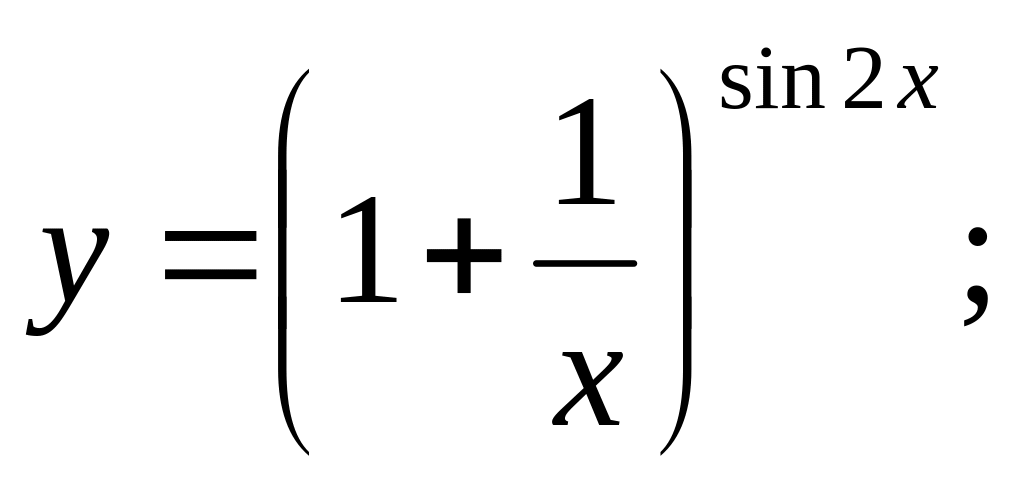 c).
c).
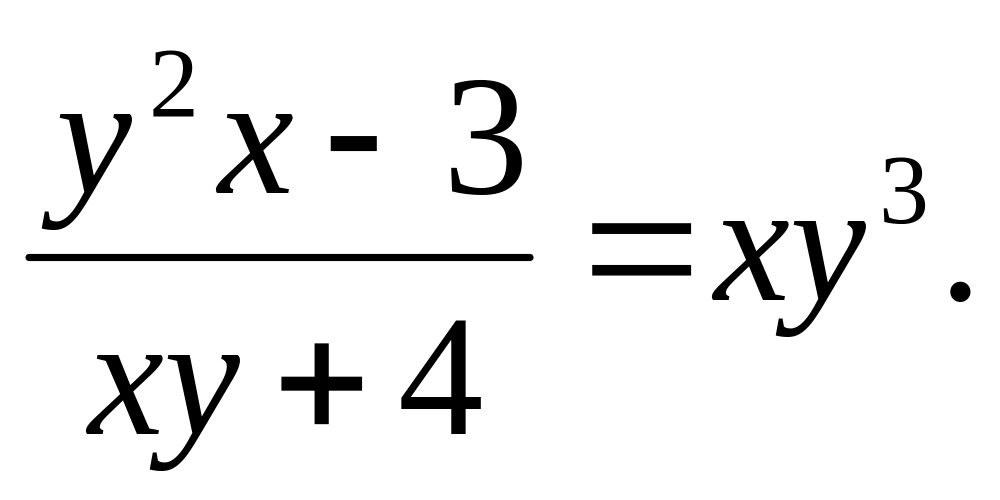
a).
 b).
b).
 c).
c).
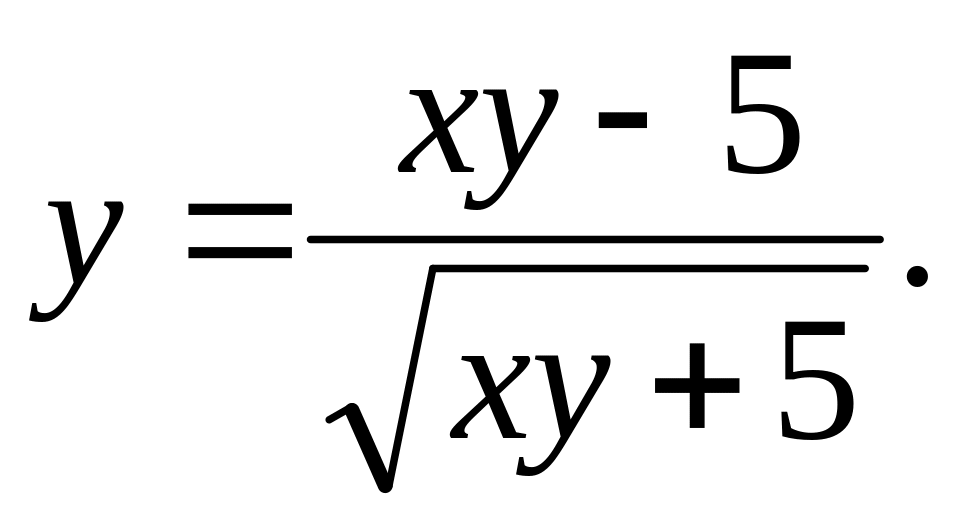
a).
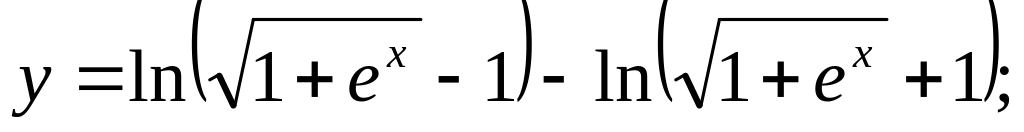 b).
b).
 c).
c).
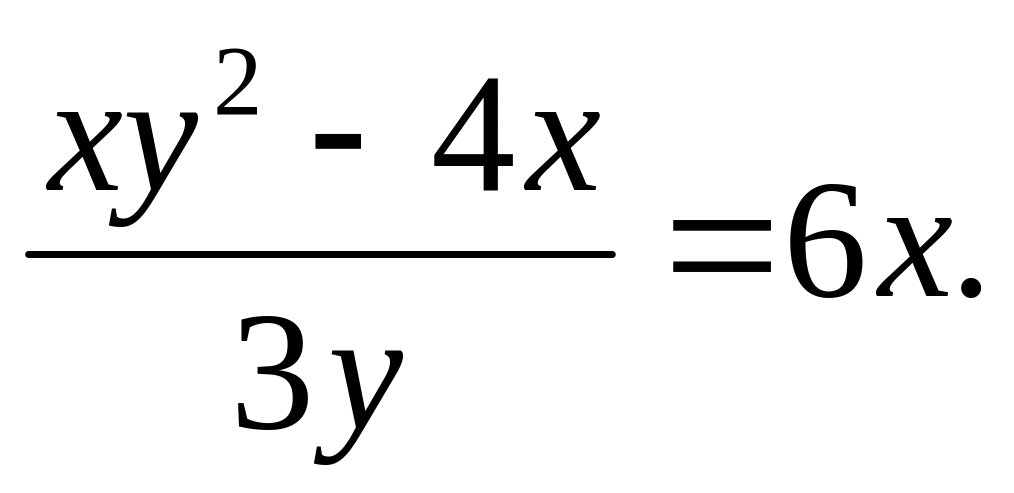
a).
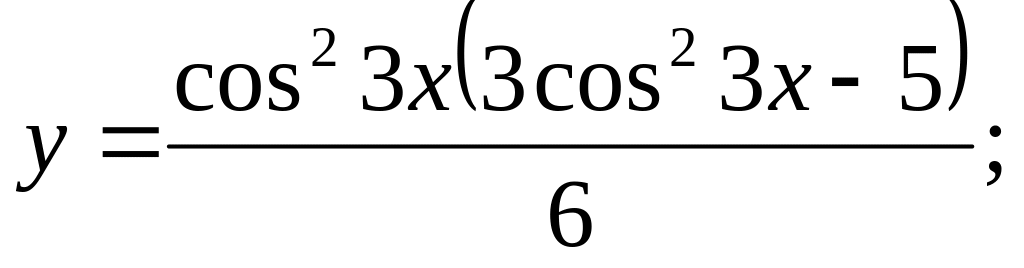 b).
b).
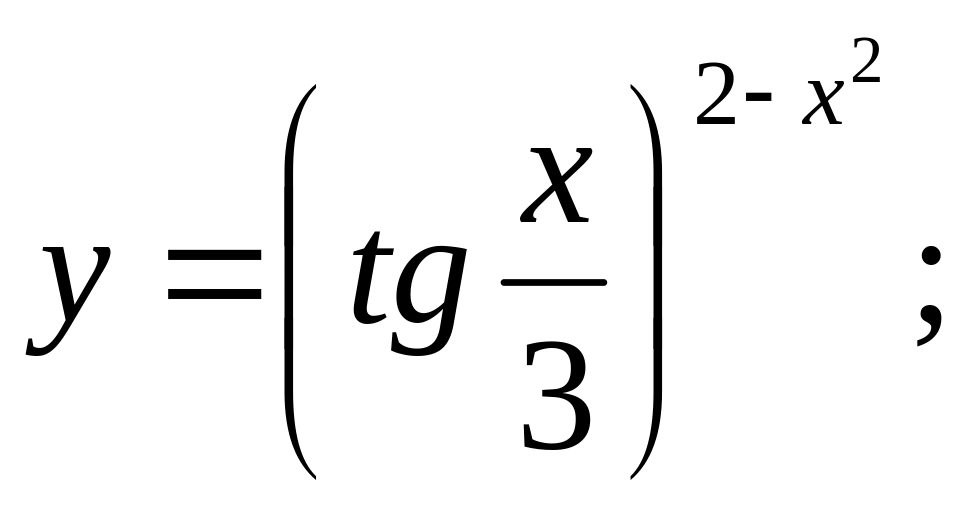 c).
c).

a).
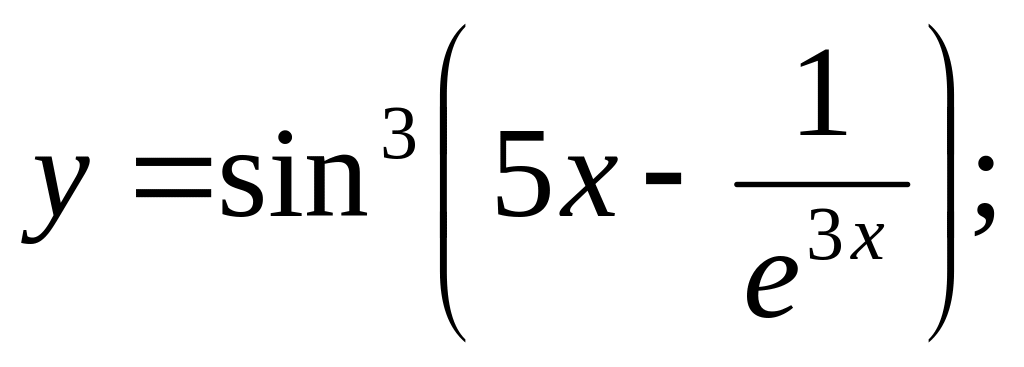 b).
b).
 c).
c).

a).
 b).
b).
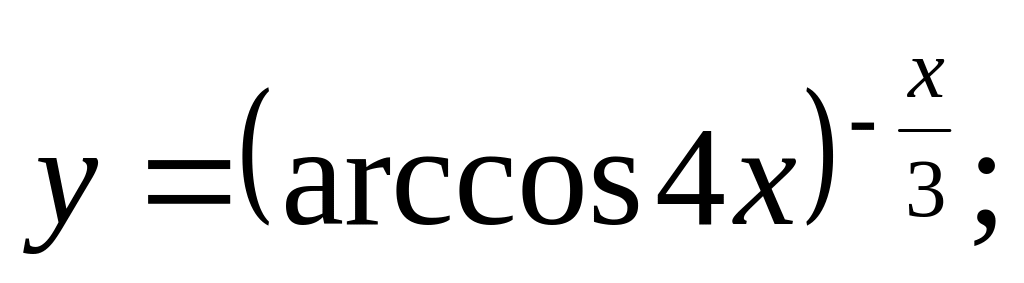 c).
c).

a).
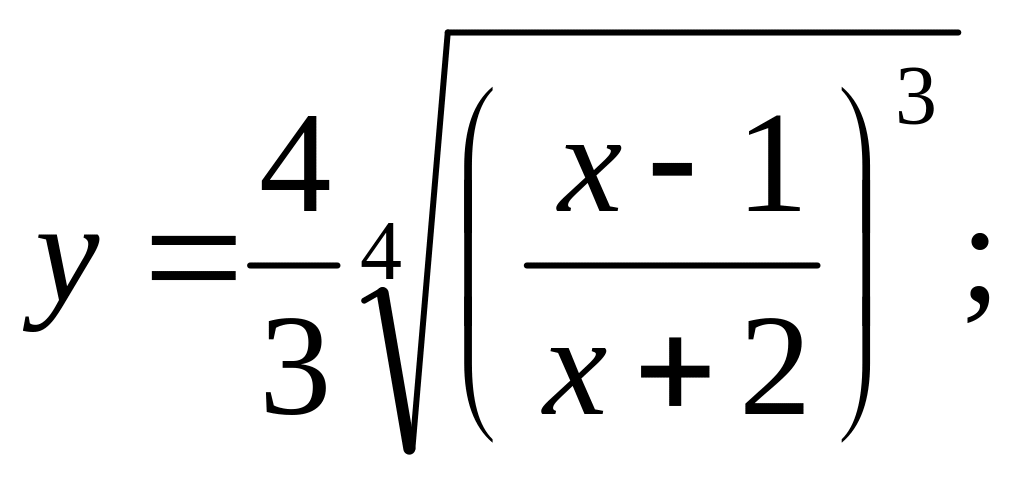 b).
b).
 c).
c).
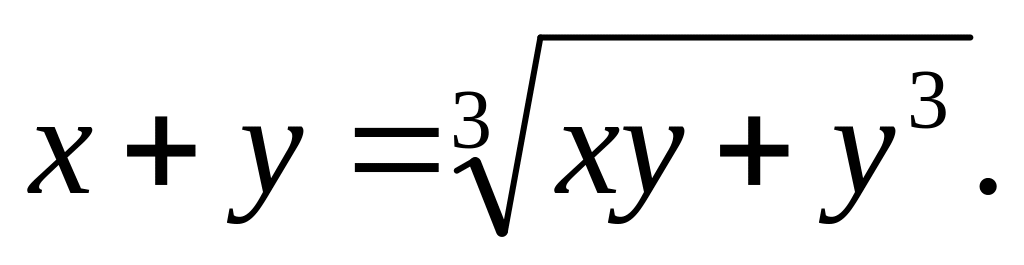
a).
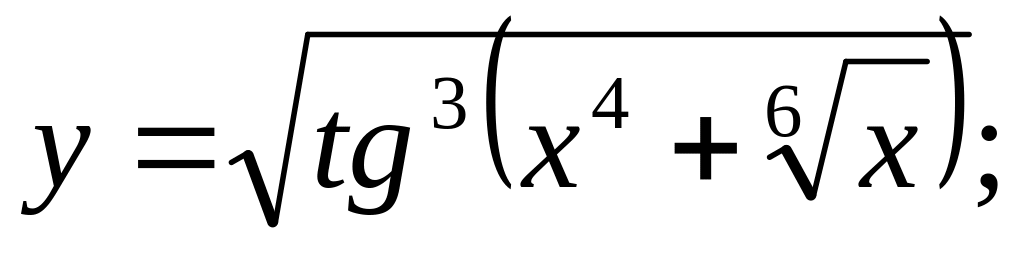 b).
b).
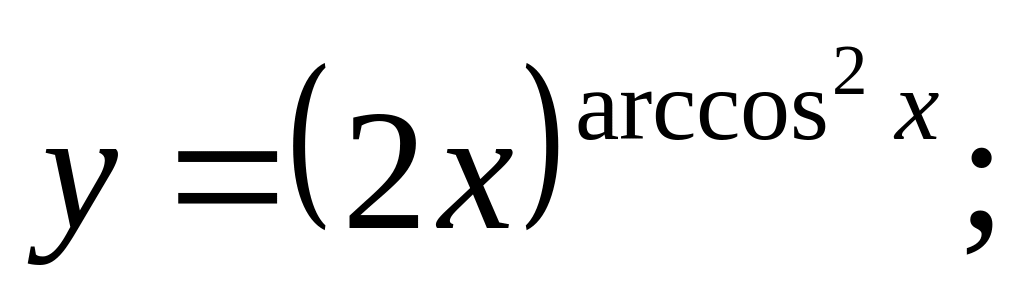 c).
c).

a).
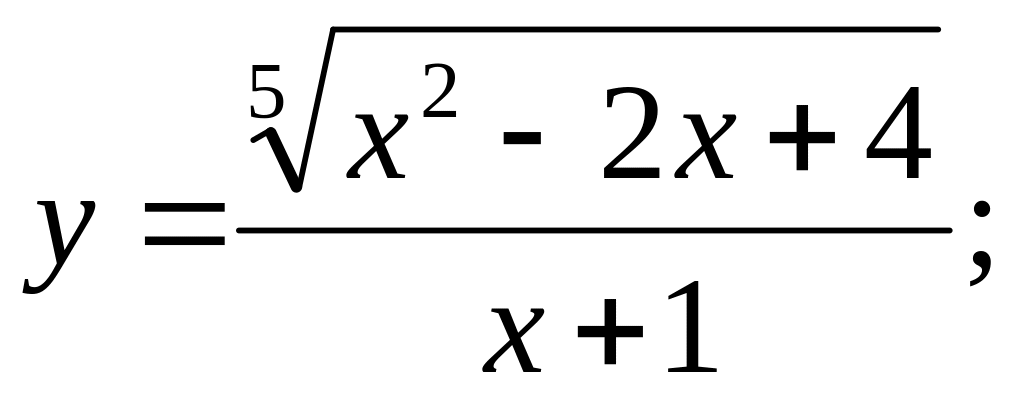 b).
b).
 c).
c).
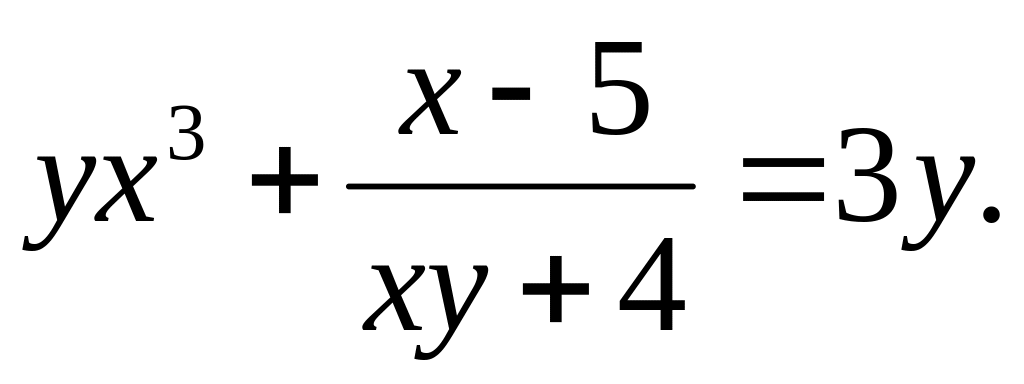
a).
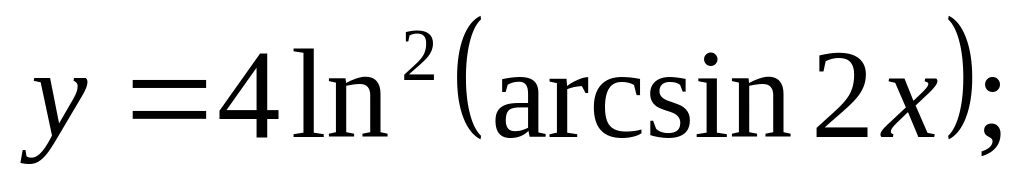 b).
b).
 c).
c).

a).
 b).
b).
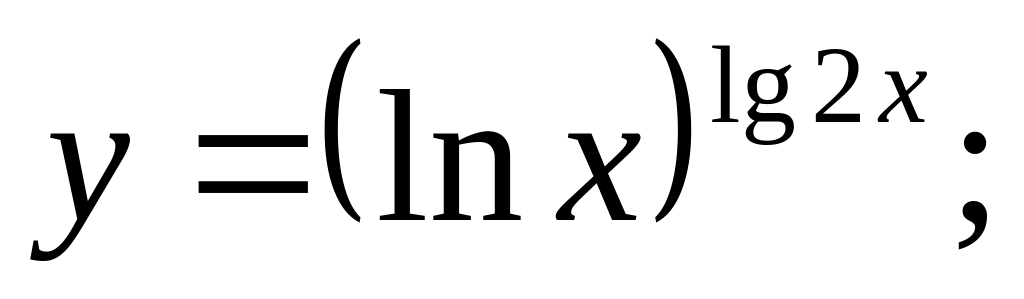 c).
c).
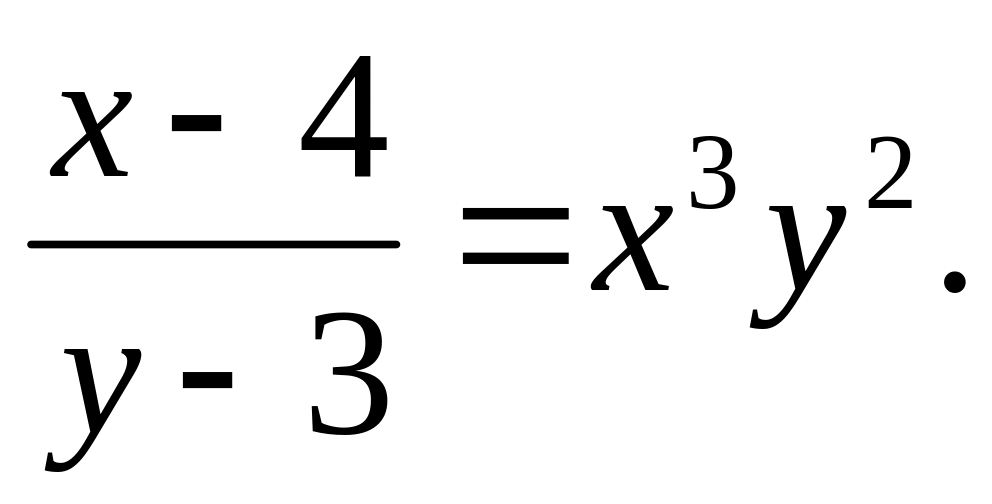
a).
 b).
b).
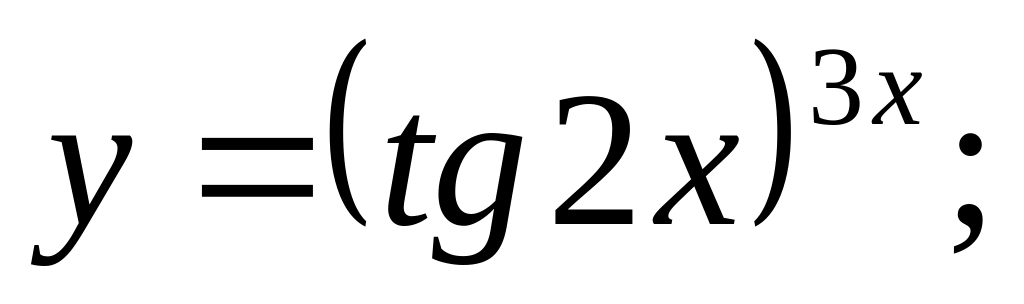 c).
c).
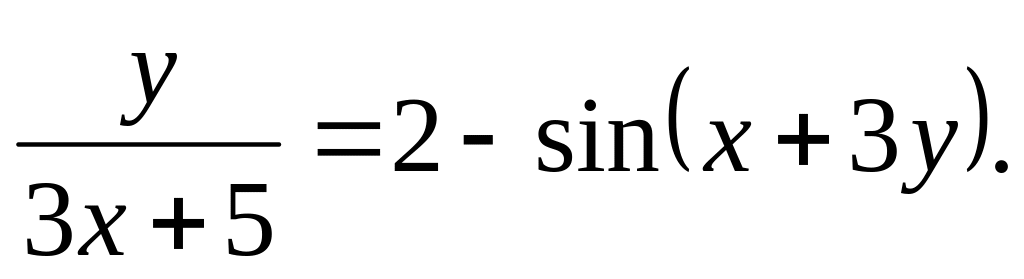
a).
 b).
b).
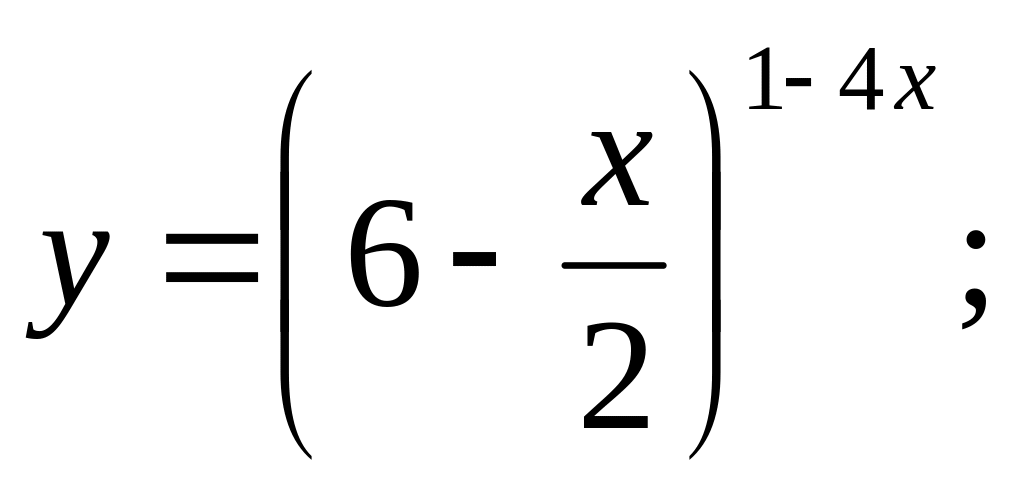 c).
c).
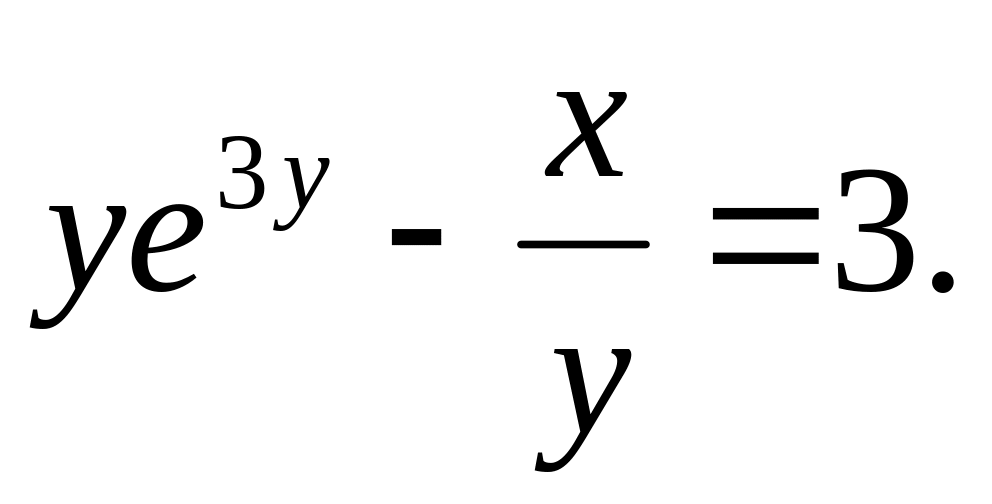
a).
 b).
b).
 c).
c).
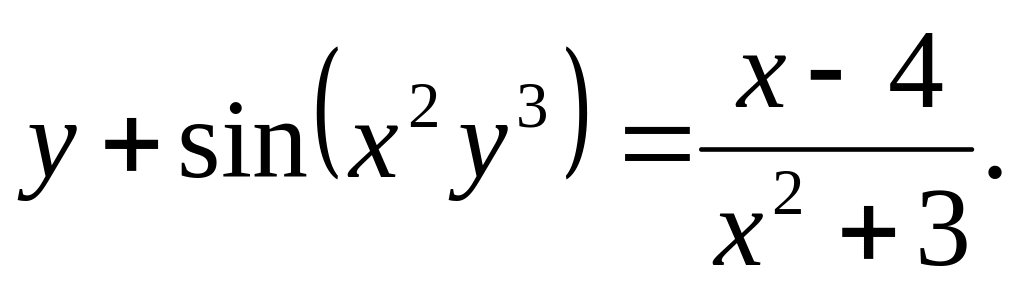
a).
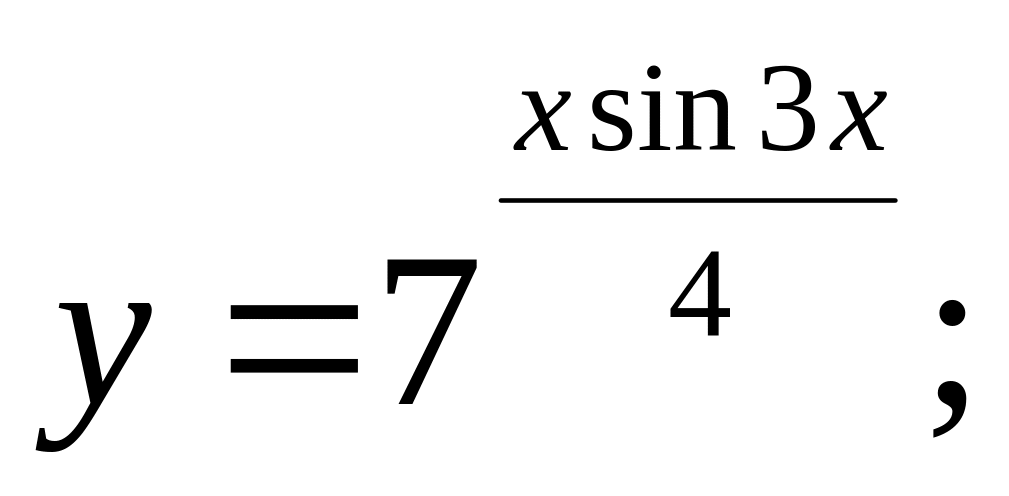 b).
b).
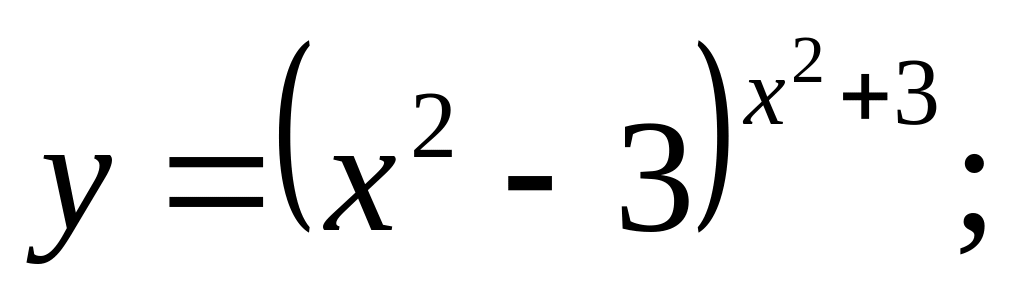 c).
c).
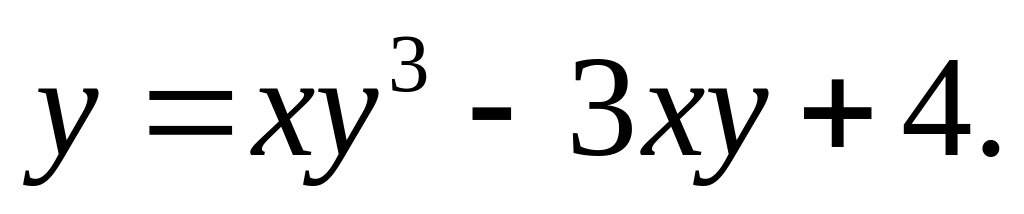
a).
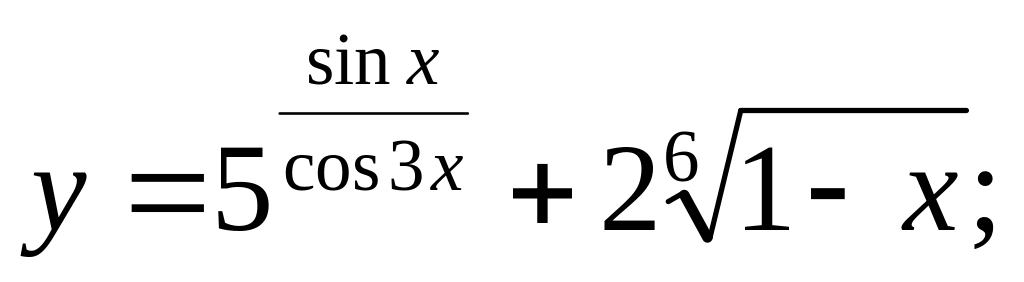 b).
b).
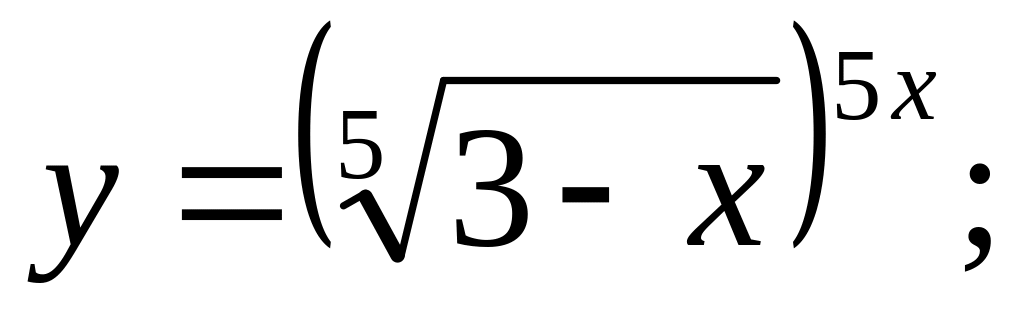 c).
c).
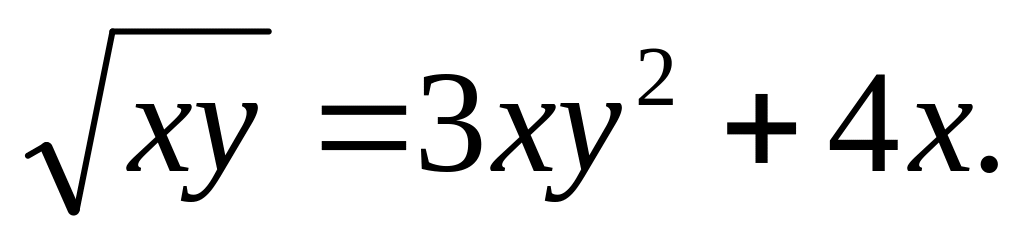
Исследовать методами дифференциального исчисления и построить графики функции:
III.
Найти производную функцию
![]() в точке
в точке
![]() в направлении, составляющем угол
с
градиентом функции
в этой точке.
в направлении, составляющем угол
с
градиентом функции
в этой точке.


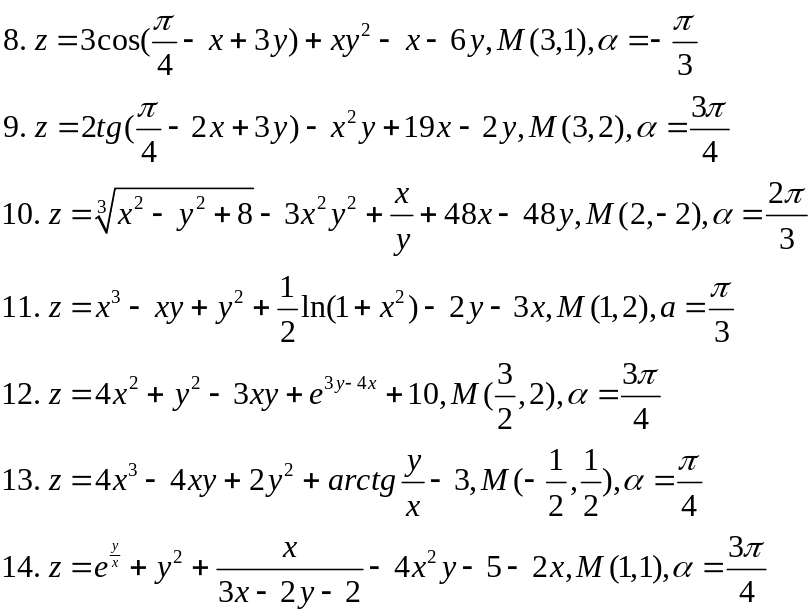

IV. Найти экстремумы функции Z=f(x,y)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
