Методические указания к выполнению контрольной работы №2

Раздел II. Дифференциальное исчисление

Задание 1. Вычисление производных

1). Производная сложной функции

Пусть дана сложная функция =F(φ(X)), причем промежуточная функция U=(φ(X)) имеет в некоторой точке X производную U’=(φ’(X)), а функция Y=F(U) - в соответствующей точке U производную Y’_u=F’(U). Тогда функция Y= F(φ(X)) имеет производную в точке X и Y’_x=F'(U)·φ или Y’_x=F'_u·U’_x, т.е. производная сложной функции равна произведению производной этой функции по промежуточной переменной на производную от промежуточной переменной по независимой переменной.

При вычислении производных удобно пользоваться таблицей производных в следующей форме (U - дифференцируемая функция от некоторой переменной).

1. Y=C Y’=0.

2. Y=U Y’=U’

3. Y=U^α(α=const) Y’=α·U^α-1·U’

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

Пример. Найти производную функцию.

т.е. где

2). Логарифмическая производная

Логарифмическая производная функции y=f(x) называется производная от логарифма этой функции, т.е. при y>0.

Нахождение производной от функций, которые допускают допускают операцию логарифмирования, значительно упрощается, если эти функции предварительно прологарифмировать, а затем воспользоваться логарифмической производной. Заметим, что логарифмическую производную будем применять формально, не учитывая, что формула имеет смысл лишь при y>0.

Пример. Найти y', если

3). Производная неявной функции

Функция y(х) называется неявной, если зависимость между х и y выражена уравнением F(x,y)=0, неразрешенным относительно y.

Чтобы найти производную от неявной функции, надо данное уравнение продифференцировать, считая y функцией от x, и вновь полученное уравнение решить относительно производной y’.

Пример. Найти y’_x, если

Задание 2. Исследование функций и построение графиков.

При построении графика функции следует:

1. Найти, область определения функции,

2. Определить четность (нечетность), периодичность функции,

3. Найти точки разрыва,

4. Определить точки пересечения графика с осями координат,

5. Найти точки экстремума я вычислить значения функции в этих точках,

6. Определить интервалы возрастания и убывания функции,

7. Найти точки перегиба, интервалы выпуклости и вогнутости,

8. Определить асимптоты,

9. Найти предельные значения функции при х стремящимся к граничным точкам области определения.

Разумеется, в процессе исследования функции не обязательно строго придерживаться приведенной схемы, иногда даже удобно изменить порядок плана.

Исследование функций с помощью производных

а). Возрастание и убывание функции

Функция f(x), определенная в некотором промежутке, возрастает в нем, если для любых двух значений x₁, и х₂ из этого промежутка неравенство x₂≥x₁, влечет за собой неравенство f(x₂)≥f(x₁).

Функция f(x), определенная в некотором промежутке, убывает в нем, если для любых двух значений x₁, и х₂ из этого промежутка неравенство x₂>x₁ влечет за собой неравенство f(x₂)≤f(x₁).

Для того чтобы дифференцируемая функция f(x), возрастала в некотором промежутке, необходимо и достаточно, чтобы ее производная была неотрицательна в этом промежутке, f’(x)≥0.

Для того чтобы дифференцируемая функция f(x) убывала в некотором промежутке, необходимо и достаточно, чтобы ее производная была неположительна в этом промежутке, f(x)≤0.

Промежутки, в которых функция возрастает (убывает), называются промежутками монотонности функции. Чтобы найти промежутки монотонности функции, необходимо:

1). Найти область определения функции.

2). Найти производную функции.

3). Приравнять производную к нулю, го есть определить ее корни, а также найти точки, в которых производная не существует, а функция существует.

4). Определить знак производной в каждом из промежутков, на которые разбивается полученными точками область определения функции.

б). Исследование функции нa экстремум

Пусть функция f(x) задана и непрерывна па отрезке [a;b] и не является в нем монотонной. Точка x₀ называется точкой локального максимума, если существует такая δ - окрестность точки x₀, что для всех точек этой окрестности выполняется неравенство f(x₀)≥f(x) (рис.1)

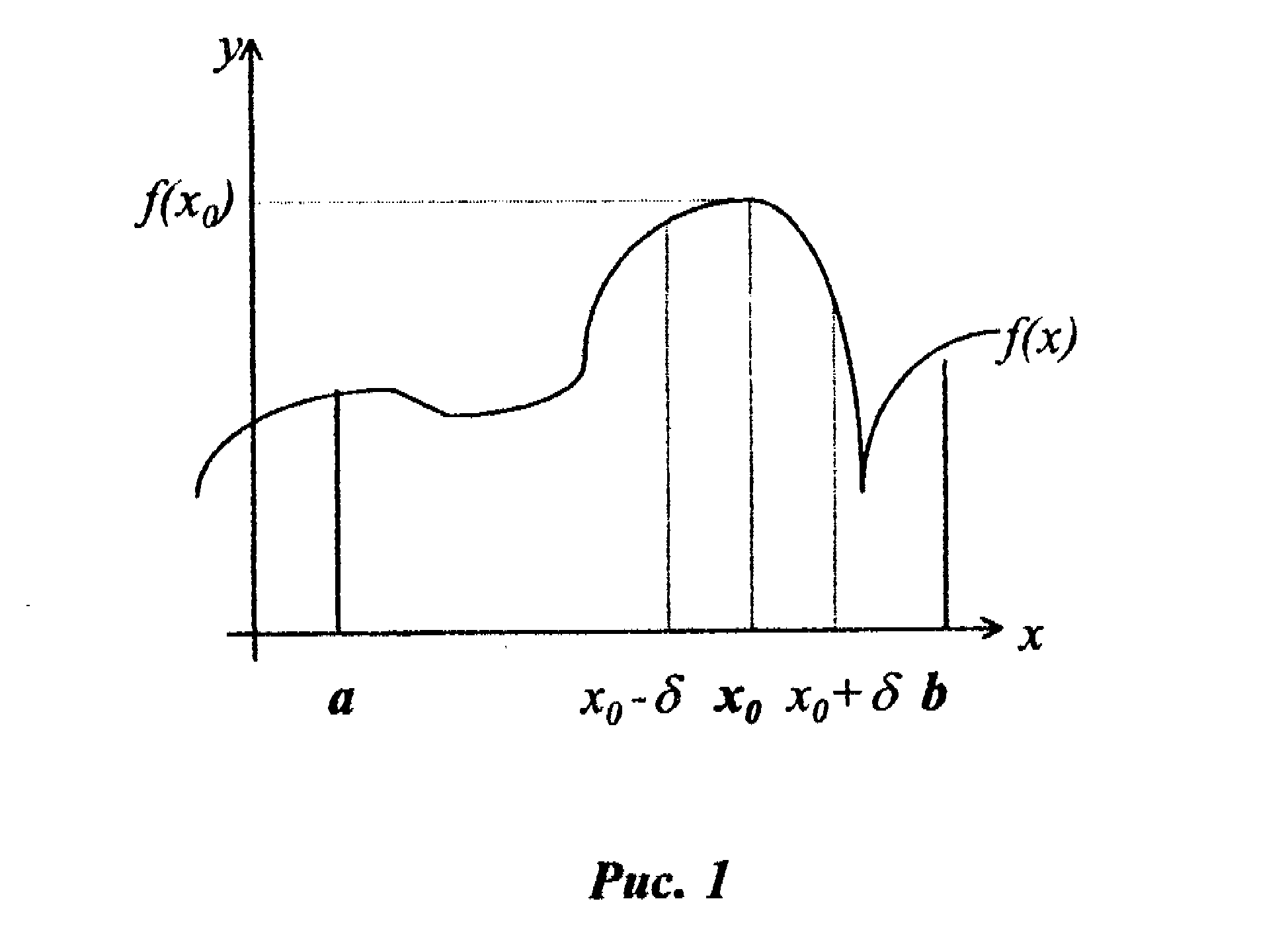
Аналогично определяется точка локального минимума.

Точка х₀ называется точкой локального минимума, если существую такая δ - окрестность точки х₀, что для всех точек этой окрестности выполняется неравенство f(x₀)≤f(x) (рис. 2).

Необходимые условия экстремума

Если функция f(x) в точке x₀, имеет экстремум, то производная f’(x₀) обращается в нуль или не существует.

Точка x₀, в которой f’(x₀)=0, называется стационарной точкой.

Достаточные признаки существования экстремума

Правило 1. Если при переходе (слева направо) через стационарную точку x₀, производная f’(x₀) меняет знак с плюса на минус, то в точке x₀ функция f’(x₀) имеет максимум; если с минуса на плюс, то минимум; если знак не меняет, то экстремума нет.

Правило 2. Пусть функция f(x) дважды дифференцируема и имеет непрерывную вторую производную в точке x₀ и в некоторой ее окрестности, тогда если f’(x₀)=0, a f’’(x₀), то в точке х₀ функция f(x₀) достигает экстремума:

1) максимума, если f’’(x₀)<0.

2) минимума, если f’’(x₀)>0.

в). Выпуклость. Вогнутость. Точки перегиба

График функции y=f(x) называется выпуклым в интервале (а, b), если он расположен ниже касательной. проведенной в любой точке этого интервала (рис. З).

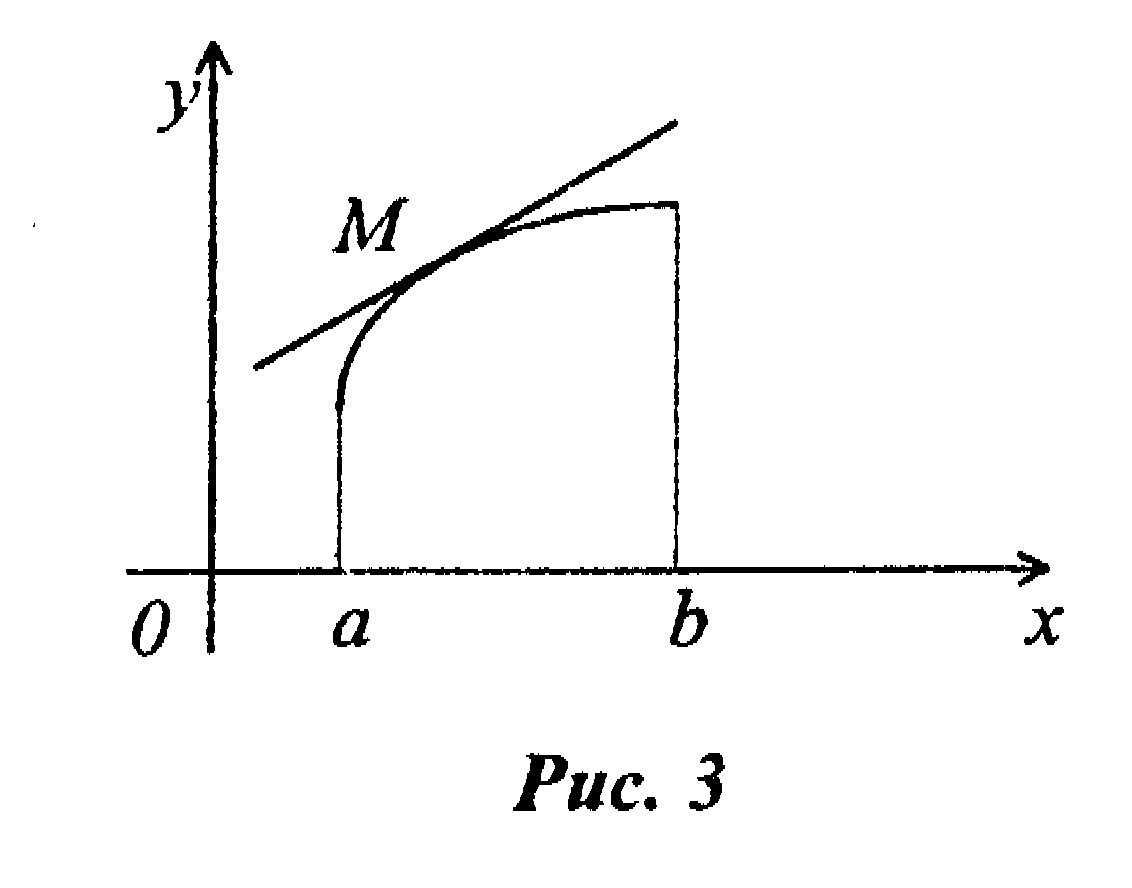
График функции y=f(x) называется вогнутым на интервале (а, b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис. 4).

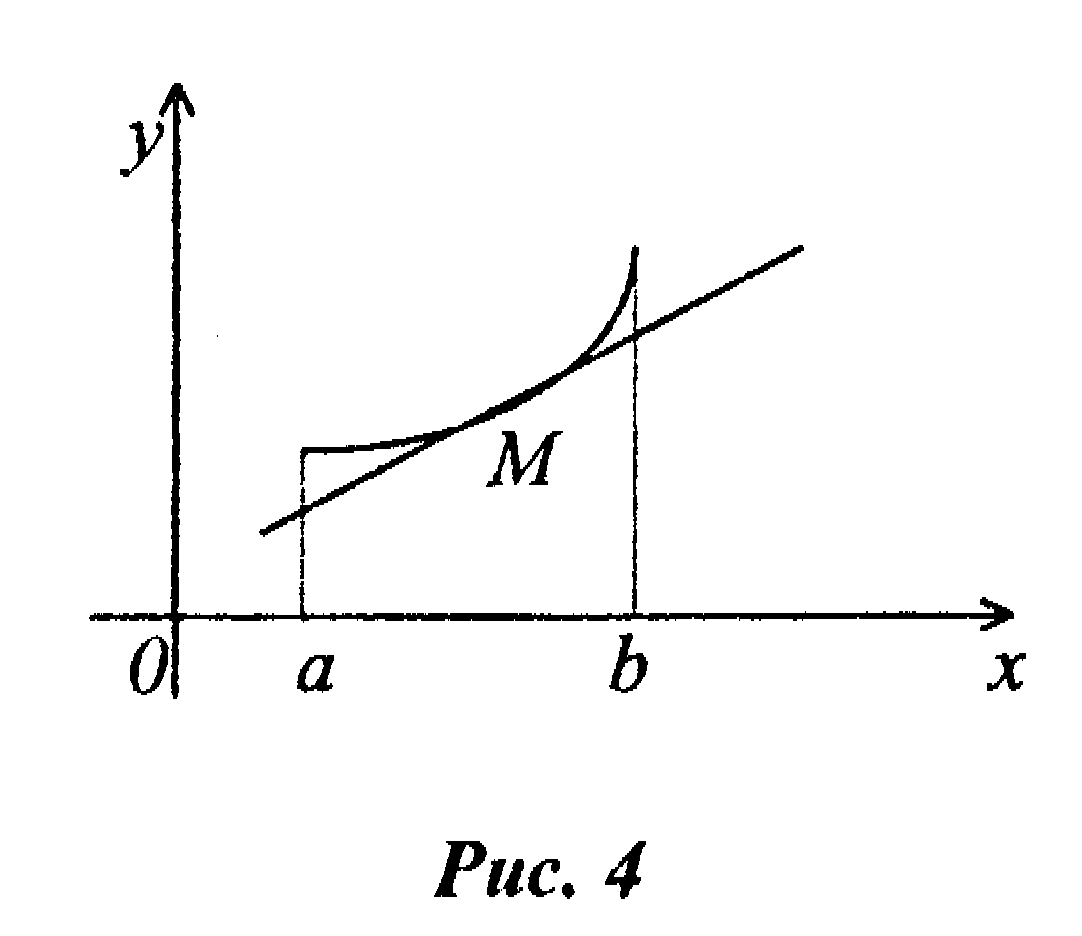
Достаточные условия выпуклости (вогнутости) графика функции.

Если f’’(x)<0 в интервале (a, b), то график функции является выпуклым в этом интервале; если же f’’(x)> 0,то в интервале (a, b) график функции - вогнутый.

Точка (x₀; f(x₀)) графика функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.

Если x₀ - абсцисса точки перегиба графика функции y=f(x₀), то вторая производная равна нулю или не существует в этой точке. Точки, в которых f’’(x₀)=0 или f’’(x₀) не существует, называются критическими точками второго рода.

Если при переходи через критическую точку второго рода x₀, вторая производная меняет знак, то точка (x₀, f(x₀)) есть точка перегиба.

г). Асимптоты

Прямая l называется асимптотой кривой y=f(x), если расстояние точки М(x,у) кривой от прямой l стремится к нулю при неограниченном удалении этой точки от кривой от начала координат, т.е. при стремлении хотя бы одной из координат точки к бесконечности.

Прямая x=а является вертикальной асимптотой кривой y=f(x), если

или .

Прямая y=b является горизонтальной асимптотой кривой y=f(x), если существует предел или

Прямая y=kx+b является наклонной асимптотой кривой у=f(x), если существуют пределы

или

Пример. Найти асимптоты кривой Функция определена при всех

Так как то прямая x=2 является вертикальной асимптотой кривой.

Горизонтальных асимптот кривая не имеет, так и .

Определим, существуют ли наклонные асимптоты. Находим

Следовательно. существует правая наклонная асимптота y=x+1.

Следовательно, существует левая наклонная асимптота у=-x-1.

Пример. Исследовать функцию и построить график.

1. Функция определена и непрерывна на всей оси ОX, за исключением точки x=-1, где она терпит бесконечный разрыв. Следовательно, прямая x=-1 является вертикальной асимптотой.

2. Точка (0;0) является точкой пересечения функции с осями координат.

3. 

Производная обращается в нуль при x=0 и x=-2.

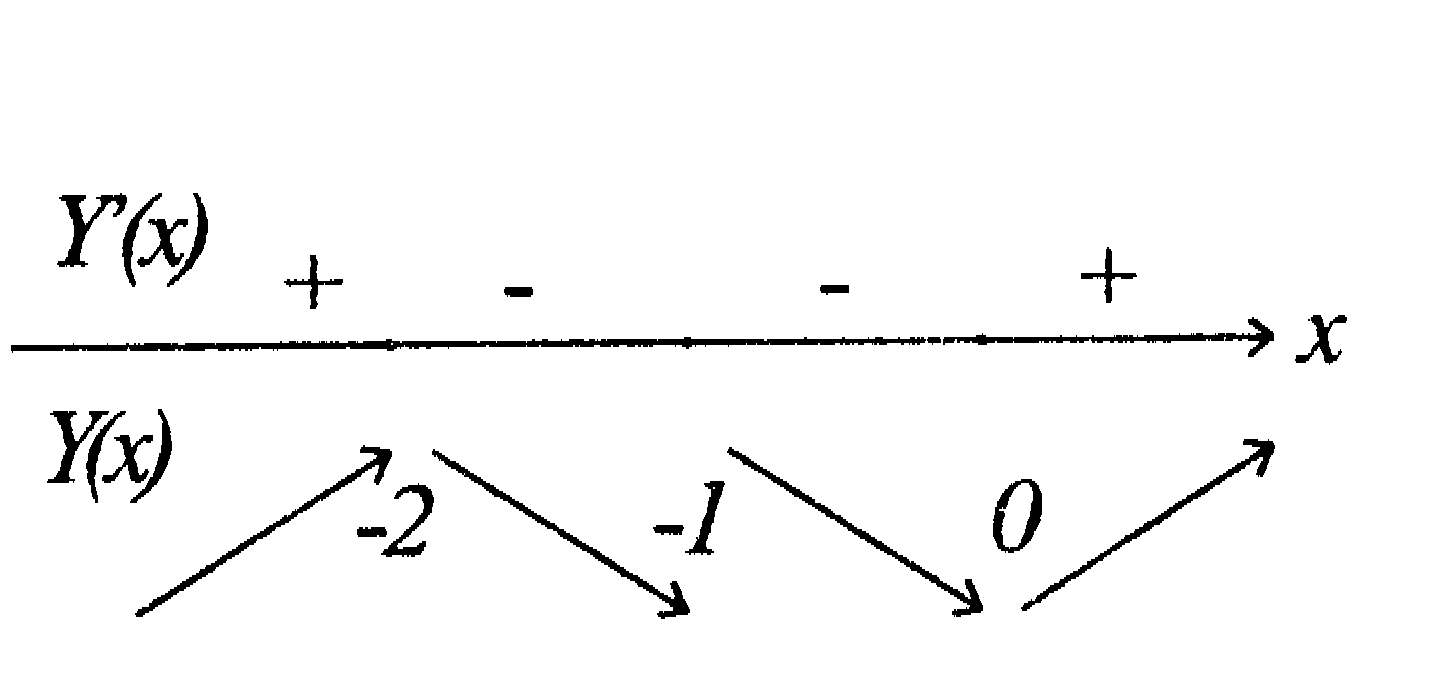
Функция возрастает при а убывает при

(-2;-4) - точка максимума, и (0,0) - точка минимума функции.

4.

Вторая производная в нуль нигде не обращается, но при преходе x через точку x=-1 меняет свой знак с минуса па плюс. Следовательно, в интервале график функции выпуклый, а в интервале - вогнутый. Точек перегиба нет.

5.Наклонные асимптоты y=kx+b, где:

Следовательно, прямая y=x-1 является наклонной асимптотой при , аналогично можно показать, что эта же прямая является наклонной асимптотой при .

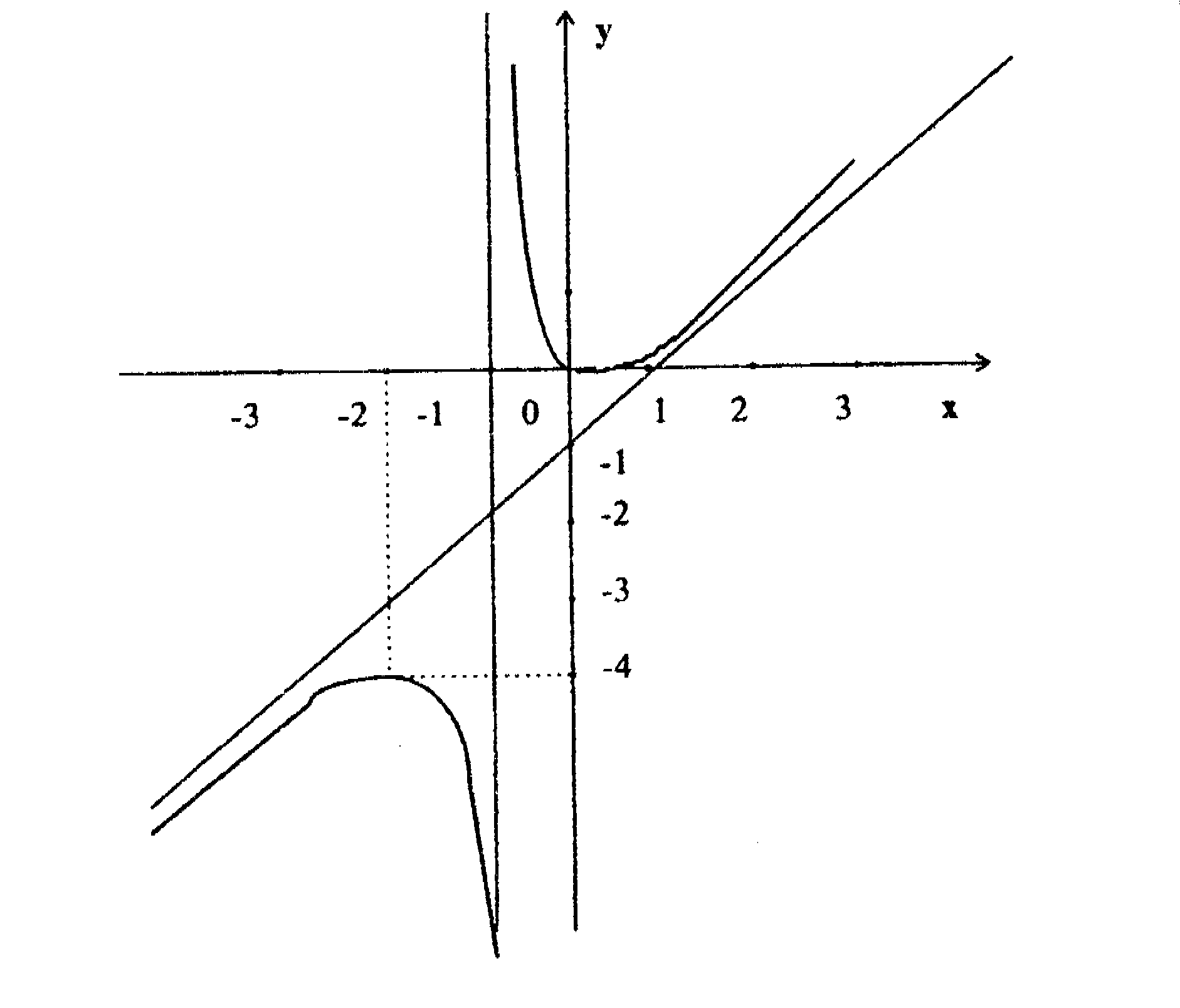
Частные производные первого порядка

Частной производной от функции z=f(x,y) по независимой переменной x называетcя производная.

, вычисленная при постоянном у.

Частной производной по y называется производная

, вычисленная при постоянном x.

Для частных производных справедливы обычные правила и формулы дифференцирования.

Пример: .

Рассматривая y как постоянную величину, дифференцируем функцию по переменной x.

Аналогично, рассматривая x как постоянную величину, получаем