Методические указания к выполнению контрольной работы №1

Указания к задаче 1

Для решения задачи 1 (прямая линия на плоскости) следует использовать следующие сведения:

1). Угол наклона прямой к оси ОХ – это тот угол, на который нужно повернуть ось ОХ, чтобы она совпала с данной прямой (или оказалась параллельной ей). Как обычно, угол положителен, если по­ворачиваем против часовой стрелки, и отрицателен, если поворачи­ваем по часовой стрелке. Будем обозначать его буквой φ.

2). Угловой коэффициент прямой - это тангенс угла наклона пря­мой к оси ОХ. Будем обозначать его буквой k. Следовательно.

k = tgφ (1)

3). Уравнение прямой с угловым коэффициентам

Если прямая не параллельна оси OY (рис. I), то ее уравнение

y=kx+b, (2)

где b - координата точки пересечения прямой с осью OY, k - угловой коэффициент прямой, (x,у) - координаты любой точки на прямой.

Если прямая параллельна оси OY (рис. 2), то ее уравнение

x=a, (3)

где a – абсцисса точки пересечения прямой с осью OX.

4). Уравнение прямой, проходящей через точку М₀(x₀,y₀) и имеющую угловой коэффициент k,

y-y₀₌k(x-x₀), (4)

где (x₀,y₀) - координаты заданной точки на прямой, k - угловой коэффициент прямой, (x,y) - координаты любой точки на прямой.

5 ). Уравнение прямой, проходящей через две заданные, точки М₁(x₁,y₁) и М₂(x₂,y₂):

(5)

где ; (x₁,y₁) - координаты одной точки на прямой, (x₂,y₂) - координаты другой точки на прямой, (x,y) - координаты любой точки на прямой.

6). Общее уравнение прямой:

Ax + By +C=0, (6)

где A, B, С - заданные числа, причем А и В одновременно в нуль не обращаются. (x,y) - координаты любой точки на прямой.

Е сли В не обращается в нуль, то уравнение (6) можно преобра­зовать следующим образом:

(6')

Тогда, сопоставив формулы (6') и (2), имеем:

7). Условие параллельности двух прямых

k₁=k₂; (7)

где k1 и k2 - угловые коэффициенты прямых.

8). Условие перпендикулярности двух прямых

k₁·k₂=-1, (8)

где k₁ и k₂ - угловые коэффициенты прямых.

9). Нахождение координат точки пересечения двух прямых.

Если две непараллельные прямые заданы своим уравнениями:

A₁X+B₁Y+C₁=0 и A₂X+B₂Y+C₂=0,

то координаты точки пересечения этих прямых - есть решение системы уравнений:

(9)

10). Нахождение координат середины отрезка

Если точка А имеет координаты (x_а,y_а), а точка В - (x_ь,y_ь), то координаты середины О отрезка АВ можно найти по формулам:

(10)

11). Нахождение длины отрезка

Е сли точка А имеет координаты (x_а,y_а), а точка В - (x_ь,y_ь), то длину отрезка АВ можно найти по формуле:

(11)

12). Свойства диагоналей параллелограмма и ромба

Диагонали в параллелограмме точкой пересечения делятся пополам. Диагонали в ромбе взаимно перпендикулярны и точкой пересечения делятся пополам.

13). Свойства средней линии треугольника

Средняя линия треугольника соединяет середины двух сторон треугольника и параллельна третьей стороне.

Рассмотрим несколько примеров применения приведенных формул.

Задача 1. Найти уравнение прямой, проходящей через точку пересечения прямых

2x+3y-12=0 и x-y-1=0 и наклонной к оси OX под углом π/4.

Решение. Найдем точку пересечения прямых 2x+3y-12=0 и x-y-1=0. Для этого следует решить систему уравнений (9):

Следовательно прямая проходит через точку М₀(3,2). Прямая наклонена к оси ОX под углом π/4, поэтому по формуле (1) найдем угловой коэффициент k=tgφ=tgπ/4=1.

Прямая проходит через точку М₀(3,2) и имеет угловой коэффициент k=1, поэтому уравнение прямой будем искать в виде (4):

y-y₀=k(x-x₀), где x₀=3, y₀=2, k=1.

Тогда получим: y-2=1(x-3)x-y-1=0.

Задача 2. Найти уравнение прямой, проходящей через точку C(3,2) и середину отрезка АВ, где А(3,5), B(-7, 9).

Решение. Найдем координаты середины отрезка АВ по формулам (10):

Подставляя x_a=3, x_b=-7, y_a=5,

y_b=9, получим: x₀=-2, y₀=7, т.е. O(-2,7) – середина отрезка AB. Прямая проходит через две точки С(3,2) и О(-2, 7), поэтому ее уравнение будем искать в виде (5):

Подставляя x₁=3, x₂=-2, y₁=2, y₂=7, получим:

Задача 3. Найти уравнение прямой, проходящей через точку С(3,2) параллельно прямой 4x+5y-2=0.

Решение. Найдем угловой коэффициент k₁ прямой 4x+5y-2=0. Для этого представим уравнение в виде (2): у=kx+b.

Следовательно,

Используя условие параллельности прямых (7), получим, что угловой коэффициент прямой

Так как прямая проходит через точку С(3,2) и имеет, то уравнение прямой будем искать в виде(4):

y-y₀₌k(x-x₀).

П одставляя x₀=3, y₀=2, получим:

Задача 4. Найти уравнение прямой, проходящей через точку пересечения прямой 2x-3y+12=0 с осью OX, перпендикулярно прямой x+2y+4=0.

Решение. Найдем угловой коэффициент k₁ прямой x+2y+4=0. Для этого представим наше уравнение в виде (2): у=kx+b.

Следовательно, Используя условие перпендикулярности прямых (8),

получим угловой коэффициент прямой

Найдем точку пересечения прямой 2x-3y+12=0 с осью OX. В точке пересечения с осью OX координата y=0 , поэтому 2x+12=0 x=-6. Получаем точку С(-6,0). Прямая проходит через точку С(-6,0) и имеет k=2, поэтому уравнение прямой будем искать в виде (4): y-y₀₌k(x-x₀).

Подставляя x₀=-,6 y₀=0, k=2 получим:

Задача5. При каких значениях «а» прямые (а-3)x+4y+1=0 и 3x+8y+1=0 перпендикулярны?

Решение. Представим уравнения прямых в виде (2): у=kx+b.

Следовательно, Воспользуемся условием перпендикулярности прямых (8):k₁•k₂=-1.

Задача 6. Найти проекцию точки А(1,1) на прямую 2x+3y+12=0.

Решение. Проекция точки на прямую - это точка пересечения данной прямой и перпендикуляра к ней, проведенного через точку А, Найдем угловой коэффициент k₁ данной прямой. Для этого представим уравнение 2х+Зу+12=0 в виде (2): у=k₁x+b.

Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух, прямых (8): k₁•k₂=-1.

Подставляя вместо k₁ угловой коэффициент данной прямой, получим:

Т ак как перпендикуляр проходят через точку А(1,1) и имеет то будем искать его уравнение в виде (4): y-y₀₌k(x-x₀). Подставляя x₀=1,y₀=1, получим:

Найдем точку пересечения прямой 2x+3y+12=0 и перпендикуляра 3x-2y+1=0, решая систему уравнений (9):

Следовательно, точка проекция точки А(1,1) на прямую 2x+3y+12=0.

Задача 7. Точки A(-2,-l), В{5,-2) и С(0,4) являются вершинами треугольника ABC. Найти точку пересечения меридиан треугольника.

Решение. Обозначим середину стороны ВС буквой M, а середину стороны АС буквой N. Тогда координаты точек M и N найдем по формулам деления отрезка пополам.

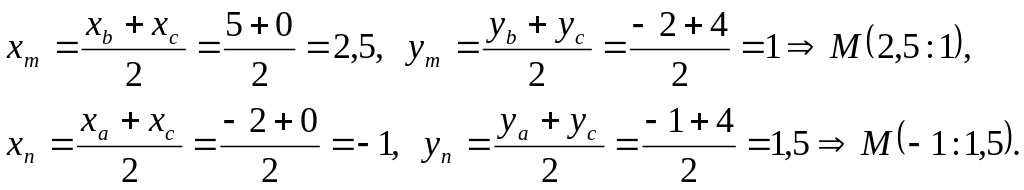
Уравнения медиан AM и AN найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AM проходит через точки

А(-2;1) и М(2,5;1), поэтому:

Медиана BN проходит через точку B(5;-2) и N(-1;1,5), поэтому:

Точку пересечения медиан AM и BN найдем из системы уравнений:

т.е. точка пересечения медиан имеет координаты .

Задача 8. При каком m прямая 5у-mx+m-2=0 проходит через точку

A(-1;2)?

Решение. Так как точка А(-1;2) принадлежит прямой, то ее координаты удовлетворяют

уравнению прямой, поэтому имеем:

Указания к задаче 2

Задача 2 связана с графическим решением системы неравенств с двумя переменными. Для решения этой задачи используются следующие соображения:

1.Любое уравнение вида определяет на плоскости некоторую прямую , делящую плоскость на две части (полуплоскости),лежащие по разные стороны от прямой. В пределах каждой из них левая часть уравнения сохраняет знак: в одной из полуплоскостей она положительна, а в другой отрицательна. Для определения знака выражения в пределах каждой из полуплоскостей достаточно вычислить его в любой точке этой полуплоскости (рис.1)

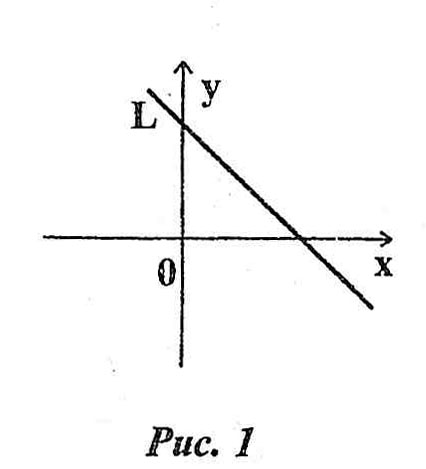
Для решения системы линейных неравенств нужно для каждого из неравенств построить соответствующую прямую и выяснить, в какой из определяемых ею полуплоскостей левая часть имеет нужный знак, а затем определить пересечение (общую часть) всех выделеных полуплоскостей.

Пример. Решить графически систему линейных неравенств и найти координаты вершин полученной области.

Решение. Начнем с рассмотрения неравенства (1) .

Прямая , соответствующая этому неравенству, описывается уравнением : .

Для ее построения найдем две точки, лежащие на прямой. Положим , тогда , т.е. прямая проходит через точку (0;4). Будем откладывать по оси абсцисс, а по оси ординат. Положим теперь , тогда , т.е. прямая проходит через точку (6;0). Нанесем эти точки на рис.2 и проведем через их прямую . В начале координат (0;0) левая часть уравнения (т.е. ) отрицательна : . Следовательно, все точки, в которых , лежат по ту же сторону от прямой , что и начало координат (0;0). На рис.2 это отмечено стрелками. Мы построили множество решений первого неравенства. Аналогично поступим с остальными неравенствами.

Прямая , соответствующая неравенству (2), описывается уравнением : .

Она проходит через точки . Нанесем эти точки на рис. 2 и проведем через них прямую .

В начале координат (0;0) левая часть уравнения (т.е. ) положительна. Следовательно, все точки, в которых , лежат по туже сторону от прямой , что и начало координат. На рис.2 это отмечено стрелками.

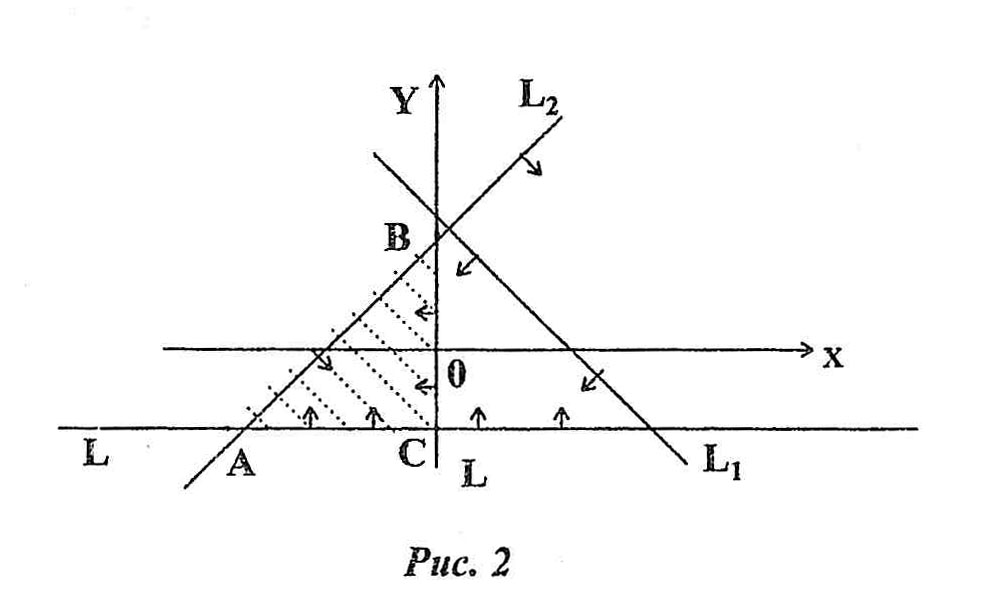
Прямая , соответствующая неравенству (3), описывается уравнением : .

Она проходит через точку и параллельна оси абсцисс. Нанесем ее на рис. 2. Вначале координат (0;0) левая часть уравнения (т.е. ) положительна. Следовательно, все точки, в которых , лежат по туже сторону от прямой , что и начало координат. На рис. 2 это отмечено стрелками.

Прямая , соответствующая неравенству (4), описывается уравнением : .На рисунке- это ось ординат. В точке (1;0) левая часть уравнения (т.е. ) положительна. Следовательно, все точки, в которых , лежат по другую сторону от прямой , чем точка (1;0). На рис.2 это отмечено стрелками.

Теперь заштрихуем ту часть плоскости, которая соответствует всем стрелкам. Получим треугольник . Из рисунка видно, что Точка является точкой пересечения прямых и , поэтому ее координаты найдем решив систему уравнений :

.

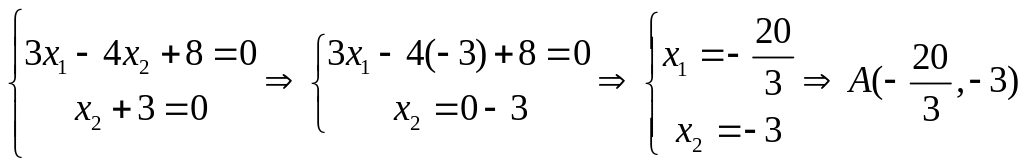Следовательно , координаты вершин нашей области :

Указания к задаче 3

Meтод Жордана

Система линейных алгебраических уравнений называется системой с базисом, если в каждом ее уравнении имеется выделенное неизвестное, не входящее ни в одно из остальных уравнений и входящее в данное уравнение с коэффициентом, равным единице При соответствующей нумерации неизвестных (в k-м уравнении выделенной служит неизвестная x_k) система с базисом имеет вид:

(A)

Выделенные неизвестные x₁, x₂……., x_m называют базисными, а остальные – свободными (небазисными).

Если члены, содержащие свободные неизвестные, перенести в правую часть, то система с базисом запишется в следующем эквивалентном виде:

(B)

Решение системы (В) получается сразу: надо придать свободным неизвестным любые значения и определить из системы (В) отвечающие им значения базисных неизвестных. Ясно, что полученный таким образом набор значений x₁, x₂……., x_m, x_m+1 ,…. x_n ,будет решением системы (В) и, тем самым, решением исходной системы (А). Также ясно, что таким образом может быть получено любое решение исходной системы. Другими словами: соотношения (В) дают общий вид решения системы (А).

П ример

В системе

базисными неизвестными служат x₂, x₅, x₆. Решая систему относительно этих неизвестных, получим:

Эти формулы дают общее решение исходной системы: при любых конкретных значениях свободных неизвестных x₁, x₃, x₄, они дают решение системы, и любое решение может быть получено таким путем. Положив, например, x₁ = x₃ = x₄=0, получим для базисных неизвестных x₂=10, x₅=8, x₆=15 и решение системы - вектор X⁽⁰⁾ = (0;10;0;0,8;15). При x₁=1, x₃=-1, x₄=4 получим значения x₂=10-3+2+2=11 , x₅=8-2-5-4=--3. x₆= 15-4+3+10=24 и решение - вектор. X⁽¹⁾ = (1;11;-1;4;-3;24).

Заметим, что решение, в котором все свободные неизвестные равны нулю, называется базисным. В нашем примере - это X⁽⁰⁾.

Решение общей системы линейных алгебраических уравнений методом Жордана заключается в планомерном преобразовании системы к эквивалентной ей системе с базисом.

А лгоритм метода опишем на конкретном примере системы: (1)

(2)

(3)

(4)

Систему рассматриваем для двух возможных значений правой части b₃, третьего уравнения b₃=15 и b₃=10.

Отдельный шаг преобразования заключается в назначении в одном из уравнений неизвестной, которая должна быть в нем базисной, и исключении ее из остальных уравнений. Этот шаг повторяется до тех пор пока это возможно (см. ниже).

Выделим в первом уравнении неизвестную х₂. Так как коэффициент при базисной неизвестной должен равняться единице, то делим обе части уравнения на коэффициент при х₁ (т.е. на -1). Получим.

-7х₁+x₂-5x₃+х₄-2x₅=-12. (1’)

Пользуясь уравнением (1’), исключим неизвестную х₂ из остальных уравнений. Для этого умножаем (1’) на - 4 и складываем с уравнением (2). Затем умножаем (1’) на 6 и складываем с уравнением (3) Затем умножаем (1') на - 2 и складываем с уравнением (4).

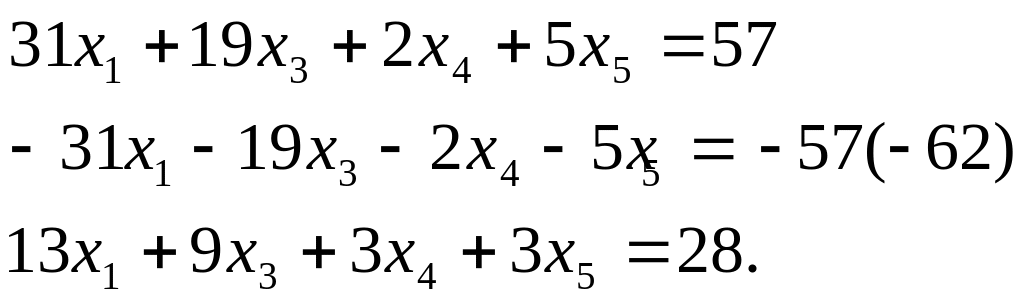(2’)

(3’)

(4’)

Базисная переменная в первом уравнении выделена. При этом получена эквивалентная система (1’) - (4’).

Аналогичным образом выбираем неизвестную х₄, а уравнении (2’) и превращаем ее в базисную и т.д. Весь алгоритм оформляется в виде последовательных преобразований (описанного выше типа) таблицы, в которой записана вся информация о системе, каждая строка таблицы дает запись одного уравнения. В первом столбце записаны правые части уравнений, в остальных - коэффициенты при неизвестных см. на с. 19 Т.1.

Каждый шаг (так называемая большая итерация) требует выполнения следующих действий:

1. Выбор главного (ключевого или ведущего) элемента

За главный элемент можно принять любой отличный от нуля коэффициент при одном из неизвестных. В каждой строке главный элемент может выбираться только один раз. Невозможность выбора главного элемента говорит об окончании вычислений. Выбранный элемент заключается в квадратик. Его строку и столбец будем называть ключевыми.

2. Преобразование ключевой строки

Все элементы ключевой строки делятся на главный элемент. На его месте возникает единица. Полезно ее подчеркнуть.

3. Назначение дополнительных множителей

Каждой не ключевой строке исходной таблицы соотносится множитель равный взятому с обратным знаком ее элементу, стоящему в ключевом столбце. Эти множители приписаны справа от таблицы.

4. Преобразование не ключевых строк

Для преобразования не ключевой строки нужно каждый элемент преобразованной ключевой строки умножить на дополнительный множитель преобразуемой строки и добавить к соответствующему элементу.

5. Если в ходе вычислений появляется строка вида:

b	x1	x2	……	xn
b≠0	0	0	…….	0

т.е. строка, в которой все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля, то система не имеет решений.

Действительно, всякое решение системы должно удовлетворять уравнению, записанному в этой строке, которое имеет вид:

Поскольку его левая часть равна нулю для любых значений x₁, x₂,…, x_n, а правая часть отлична от нуля, то ему не может удовлетворять ни один такой набор.

6. Если в ходе вычислений появляется строка, состоящая из одних нулей, то ее можно удалить из таблицы, так как такая строка отвечает уравнению:

которому удовлетворяет любой набор значений x₁, x₂,…, x_n и поэтому ее можно не учитывать.

Заметим, что появление строки из одних нулей свидетельствует о том, что записанное в ней уравнение является следствием других уравнений системы.

Если при применении алгоритма не возникает противоречивой ситуации, описанной в п.5, то в каждой строке заключительной таблицы (т.е. в каждом уравнении) имеется базисная неизвестная, и система оказывается приведенной к эквивалентной системе с базисом.

Применим описанный алгоритм к системе из примера.

b	x1	x2	x3	x4	x5	Доп.множитель.
12 9 15(10) 4	7 3 11 -1	-1 4 -6 2	5 -1 11 -1	1 6 -8 5	2 -3 7 -1	- -4 6 -2
-12 57 57(-62) 28	-7 31 -31 13	1 0 0 0	- 5 19 -19 9	1 2 -2 3	-2 5 -5 3	-1 - 2 -3
-40,5 28,5 0(-5) -57,5	-22,5 15,5 0 -33,5	1 0 0 0	-14,5 9,5 0 -19,5	0 1 0 0	-4,5 2,5 0 -4,5	4,5 -2,5 - -
17 -31/9 115/9	11 -28/9 67/9	1 0 0	5 -4/3 19/3	0 1 0	0 0 1

Т.1

*

Т.2

*

*

Т.3

*

Т.4*

*

В Т.1 за главный элемент выбран коэффициент при x₂ в 1-м уравнении. В Т.2 соответствующая строка помечена звездочкой в знак того, что в ней выбирался главный элемент. Затем эта строка умножается на соответствующие множители и добавляется к строкам исходной таблицы.

Дальнейшие действия аналогичны и понятны из приведенных таблиц.

В Т.З появляется строка, в которой все коэффициенты при неизвестных равны нулю.

Если в исходной таблице свободный член b₃=10, то появилась противоречивая строка,

Следовательно, система не имеет решений.

Если же b₃ = 15, то третья строка таблицы Т.З состоит из одних нулей и удаляется из таблицы.

Дальнейшее решение (Т.4) касается только этого случая.

В Т.4 все строки помечены звездочками, т.е. главный элемент появлялся, в каждой из них, и выбор его, более невозможен.

Работа алгоритма закончена. Т.4 дает запись системы с базисом, эквивалентной исходной:

Общее решение последней, а значит, и исходной системы даете формулами:

Например, при x₁=1 и x₃=1 получаем x,=1, x₄=1, x₅=1 т.е. получаем решение X=(1;1;1;1;1). Положив x₁=x₃=0 получаем базисное решение X_баз.=(0;17;0;-31/9;ll5/9), В заключение этого пункта отметим, что метод Жордана позволяет полностью исследовать любую систему линейных алгебраических уравнений.

а) если в ходе вычислений появляется «противоречивая строка»

b≠0

0

0

……..

0

то система не имеет решений. Уравнение, отвечающее этой строке, противоречит уравнениям, строки которых помечены звездочками (т.е. в которых выделялся главный элемент);

б) если «противоречивая строка» в ходе вычислении не появлялась, то система имеет решение. Его общий вид получается из последней таблицы. Если есть свободные неизвестные, то система имеет бесконечно много решений. Если свободных переменных нет, то система имеет единственное решение;

в) появление нулевой строки показывает, что соответствующее ей уравнение является следствием уравнений, помеченных звездочками в данной таблице. Число независимых уравнений равно числу ненулевых строк последней таблицы (в случае разрешимости системы).

Указания к задаче 4

Задача 4. связана с действиями над матрицами. Для решения этой задачи следует использовать следующие сведения:

1. Всякая система m·n, расположенных в виде прямоугольной таблицы, содержащей

m строк и n столбцов, называется матрицей размера m×n и записывается в виде:

2). Матрица размера m×m (количество строчек равно количеству столбцов) называется квадратной матрицей порядка m.

3). Диагональ квадратной матрицы, идущая от левого верхнего утла к правому нижнему, называется главной диагональю, а вторая диагональ называется побочной.

4). Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные цифры нули, называется единичной матрицей n, обозначается следующим образом:

5) Две матрицы одной размерности равны друг другу, если равны все элементы этих матриц, стоящие на одинаковых местах, т.е. если

6). Произведением матрицы

на число α называется матрица C_m×n, каждый элемент которой равен произведению соответствующего элемента матрицы A_m×n на число α.

7). Суммой двух матриц одной размерности

называется матрица Cm×n той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц A_m×n и B_m×n , т.е.

8). Умножение матрицы на матрицу

Пусть даны две матрицы A_m×n и B_n×k, таких что число столбцов матрица А равно числу строк матрицы В. Тогда произведением матриц называется матрица C_m×k, каждый элемент которой c_ij равен сумме попарных произведений элементов i–й строки матрицы А на соответствующие элементы j-го столбца матрица В, т.е.

Заметим, что A·B≠B·A

9). Определители квадратных матриц

Каждой квадратной матрице ставится в соответствие число, обозначаемое

Рассмотрим определителя для матриц первого, второго и третьего порядков:

а). Пусть А=(а₁₁), тогда Δ_А=│a₁₁│=a₁₁. (1)

Из формулы (1) следует, что определитель для матрицы первого порядка совпадает с элементами матрицы А_1·1.

б). Пусть (2)

Из формулы (2) следует, что определитель для матрицы второго порядка, равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.

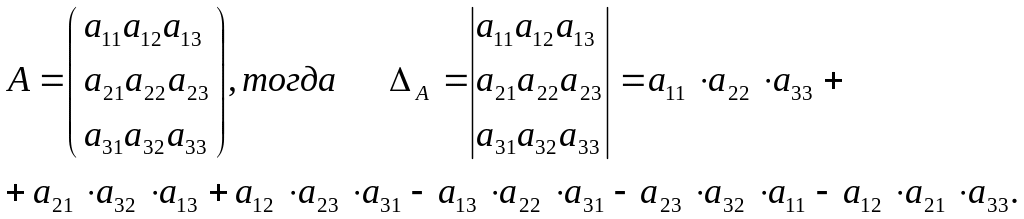
в). Пусть (3)

Формулу (3) запомнить значительно труднее, чем (1) и (2), но это и не требуется, так как существуют различные правила, позволяющие легко подсчитать те шесть слагаемых, из которых состоит определитель для матрицы третьего порядка.

Например, можно использовать «правило треугольников», которое условно показано на схемах 1 и 2.

Первые три слагаемые, входящие в формулу (3) со своим знаком, подсчитываются в соответствии со схемой 1, а следующие три слагаемые, входящие с противоположным знаком, подсчитываются по схеме 2.

10). Алгебраическим дополнением элемента а_ij квадратной матрицы A_m×n называется число А_ij, вычисляемое по формуле:

A_ij=(-1)^i+j·M_ij, где M_ij- определитель, полученный из определителя матрицы A_m×n удалением строки с номером i и столбца с номером j .

11). Обратная матрица

Матрица А^-1 называется обратной к матрице А, если A·A^-1=A^-1·A=E , где Е - единичная матрица. Из определения следует, что матрицы А и А^-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от

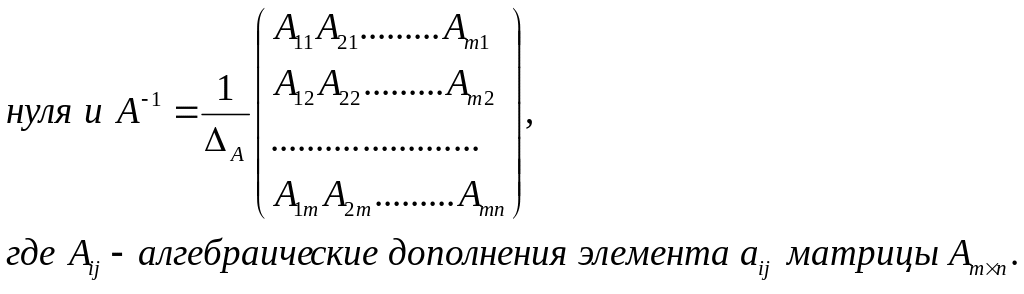
12). Решение простейших алгебраических уравнений

а) А·X=В, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X=А^-1·В.

б) X·А=В, - где ,А и В заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X= А^-1·X.

Примеры

1). Выполнить действия: (А+2В)·С, где

Решение

2). Найти А^-1, если

Решение

Тогда

Проверим, верно ли нашли А^-1. Для этого умножим А на А^-1 и убедимся, что получим единичную матрицу.

3). Решить уравнение AX-B=C, где

Решение

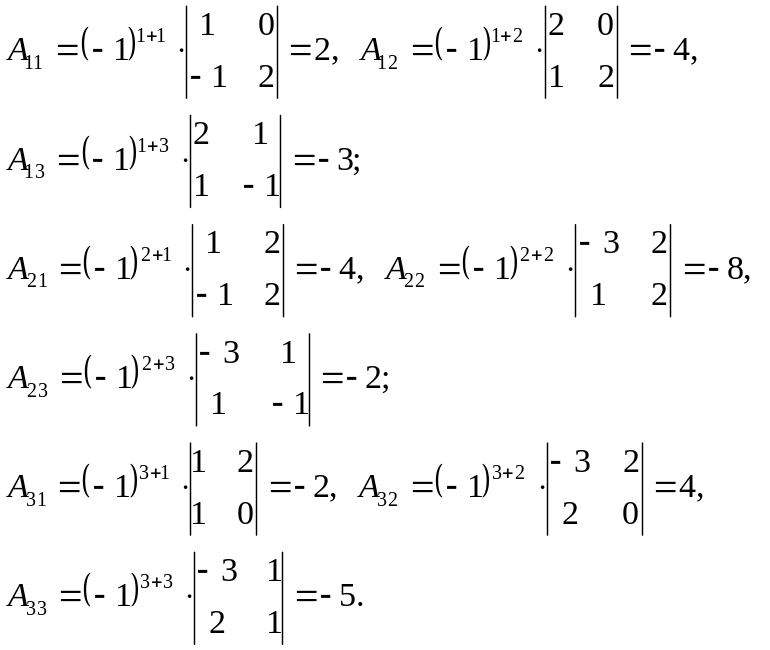
Тогда

Проверка