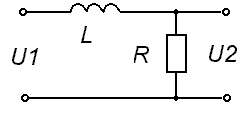
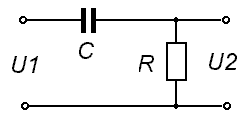
- •8. Для приведенной на рисунке схемы электрической цепи, пользуясь методом контурных токов, записать формулы, по которым рассчитываются элементы матрицы.
- •9. Для приведенной на рисунке схемы электрической цепи, пользуясь методом узловых напряжений, записать формулы, по которым рассчитываются элементы матрицы.
- •10. Для приведенной на рисунке схемы электрической цепи рассчитать операторную передаточную характеристику. Для этой цепи построить ачх.
- •Спектр периодической последовательности прямоугольных импульсов
- •13. Для приведенного на рисунке n – p- n бт, включенного в схеме соб определить все токи и напряжения в схеме.
- •14. Для приведенного на рисунке n – p- n бт, включенного в схеме соэ определить все токи и напряжения в схеме.
- •Упрощенная структура полевого транзистора с управляющим затвором в в виде р –n перехода
- •27. Для приведенной на рисунке схемы простейшего оконечного усилителя рассчитать мощность, выделяемую в нагрузке, потребляемую от источника питания, а также кпд усилительного каскада.
1. Для гармонического колебания, приведенного в алгебраической форме U=4+j4, записать выражение для комплексной амплитуды и изобразить полученную амплитуду на комплексной плоскости в виде вектора и временной диаграммы.
В электротехнике
гармонический процесс характеризуют
с помощью комплексной амплитуды.
Комплексная амплитуда – это вектор на
комплексной плоскости. U=4+j4![]() U=a+jb.
На рисунке Im
– ось мнимых, Re
– ось вещественных.
U=a+jb.
На рисунке Im
– ось мнимых, Re
– ось вещественных.

Находим максимальное значение амплитуды:
Um=![]() (В)
(В)
Находим начальную фазу напряжения:
![]() =
arctg
b/a
= arctg
4/4 = 450
=
=
arctg
b/a
= arctg
4/4 = 450
=
![]()
![]() -
-
комплексная амплитуда.
2. Для варианта графика импульсного сигнала (осциллограммы) u(t) и записать математическую модель сигнала, выраженную через временные отрезки (интервалы).
-
Сигнал S(t)
-2-
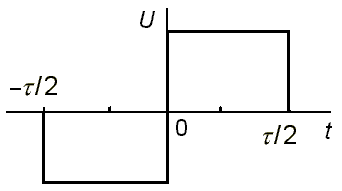
Ответ: Математическая модель может быть задана в виде аналитического выражения, графиков, таблиц. Наиболее часто используется для изучения реальных импульсных сигналов их представление в виде математических зависимостей, аргументом которых является время.
Математическую модель импульсного сигнала в электротехнике и электронике можно записать выражением, представляющим сигнал на временных интервалах (отрезках) в виде системы функций, описывающих зависимость сигнала от времени.
 0,
t
є (
0,
t
є (![]() )
)
U(t)= -Um,
t є
[![]() ;
0]
;
0]
Um,
t є
(0;![]() )
)
0, t
є [![]() )
)
-
Сигнал S(t)
-4-
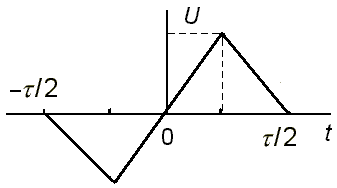
Решение:
 ;
;
 ;
;
![]()

 ;
;
 ;
;

 ;
;
 ;
;

О твет:
0, t
є (
)
твет:
0, t
є (
)
,
t
є
[
;![]() ]
]
U(t)=
,
t
є
(
;![]() )
)
, t є [ ; ]
0, t є ( )
3. Для модели аккумулятора с параметрами
-
№
варианта
Модель аккумулятора
Тип
Энергоемкость (ампер-часы)
Начальное
напряжение, В
Конечное
напряжение, В
-1-
-2-
-3-
-4-
-5-
-6-
1
SNN5636
NiMH
0.8
4.2
3.6
2
APB-34N
NiCd
1.8
5.6
4.8
3
Sony
(графит-2)
Li-ion
1.6
4.2
2.5
4
Sony (кокс)
Li-ion
1.6
4.2
2.5
определить:
а) Номинальный (рекомендуемый) ток заряда батареи. б). Требуемое время заряда батареи. в). Номинальный ток разряда (рабочий ток) батареи.
Решение. а) Для расчета номинального (рекомендуемого) тока заряда батареи воспользуемся формулой:
Iзар = Q/10=0.8/10=0.08 А/ч.
Iзар = Q/10=1.8/10=0.18 А/ч.
Iзар = Q/10=1.6/10=0.16 А/ч.
Iзар = Q/10=1.6/10=0.16 А/ч.
б) При зарядке аккумуляторов требуется, чтобы полученный заряд составлял примерно 140 % от энергоемкости батареи. Поэтому требуемое время заряда батареи можно определить из соотношения:
1) tзар = 1.4Q/Iзар=1.4*0,8/0,08=14ч.
2) tзар = 1.4Q/Iзар=1,4*1,8/0,18=14ч.
3) tзар = 1.4Q/Iзар=1,4*1,6/0,16=14ч.
4) tзар = 1.4Q/Iзар=1,4*1,6/0,16=14ч.
в) Номинальный (рекомендуемый) ток разрядки (рабочий ток) аккумулятора вычисляется по формуле
1) Iраз = 1.4Q/tзар = 1.4*0.8/14 = 0.08А.
2) Iраз = 1.4Q/tзар = 1.4*1.8/14 = 0.18А.
3) Iраз = 1.4Q/tзар = 1.4*1.6/14 = 0.16А.
4) Iраз = 1.4Q/tзар = 1.4*1.6/14 = 0.16А.
4. Для варианта гармонического напряжения, приведенного в алгебраической форме U=10+j10, величины частоты f1=100/6,28 Гц и емкости С= 100 мкФ: а) построить векторную диаграмму тока и напряжения на конденсаторе. б) построить графики зависимости модуля комплексного сопротивления конденсатора от частоты. Расчет выполнить в диапазоне частот от 30 Гц до 1 кГц. Используя графики подтвердить, что емкостной элемент обладает заградительно - шунтирующим свойством.
Решение.
Амплитудное
значение тока:
 .
Сопротивление на емкостном элементе:
.
Сопротивление на емкостном элементе:

Комплексная
амплитуда – это вектор на комплексной
плоскости.
![]() ,
где
,
где
![]() ,
,
а
![]() .
Отсюда, комплексная амплитуда равна:
.
Отсюда, комплексная амплитуда равна:
![]() .
.
Итак,

Строим векторную диаграмму тока и напряжения на конденсаторе.
Im
UC
10
IC
1/10





Re
10
-1/10
Cтроим график зависимости модуля комплексного сопротивления конденсатора от частоты.
ZC



Шунтирующее св-во

w
5. Для варианта гармонического напряжения, приведенного в алгебраической форме U=100+j100, величины частоты f1=100/6,28 Гц и индуктивности L= 100 мкГн: а) построить векторную диаграмму тока и напряжения на индуктивности б) построить графики зависимости модуля комплексного сопротивления индуктивности от частоты. Расчет выполнить в диапазоне частот от 30 Гц до 1 кГц. Используя графики подтвердить, что индуктивность обладает заградительно - шунтирующим свойством.
Решение. Амплитудное
значение тока:
 .
Сопротивление на индуктивном элементе:
.
Сопротивление на индуктивном элементе:

Комплексная
амплитуда – это вектор на комплексной
плоскости.
,
где
![]() ,
,
а
![]() .
Отсюда, комплексная амплитуда равна:
.
Отсюда, комплексная амплитуда равна:
![]() .
.
Итак,

Строим векторную диаграмму тока и напряжения на индуктивности.
Im
IC
104![]()
UC
100


Re
-104
100-
Строим график зависимости модуля комплексного сопротивления индуктивности от частоты.
ZL

w
6. Для приведенной на рисунке схемы пользуясь понятием о делителе напряжения, величину напряжения на резисторе R2 в случае, когда R1=5 Ом, R2=15 Ом, R3=1 Ом, а ЭДС и внутренние сопротивления элементов питания r1=3 Ом, E1=1 В, r2=2 Ом, E2=24 В.
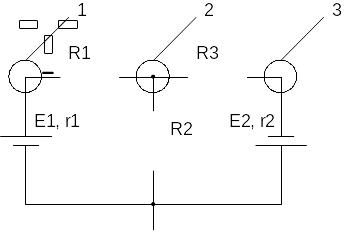

Решение: Два последовательно соединенных элемента образуют простейший делитель напряжения. Так как нам дан реальный источник ЭДС для решения задачи представим его идеальным:

Для анализируемой цепи при гармоническом входном сигнале амплитуда напряжения на резисторе R2 равна
![]()
Для второго случая
R3
R2




r2

E2

![]()
7. Для приведенной на рисунке схемы найти ток, отдаваемый источником в электрическую цепь, а затем, пользуясь понятием о делителе тока, для схемы электрической цепи и величин элементов схемы ( R1=5 Ом, R2=15 Ом, R3=1 Ом, r1=3 Ом, а ЭДС , E1=100 В, рассчитать амплитуду тока, протекающего через резистор R1.
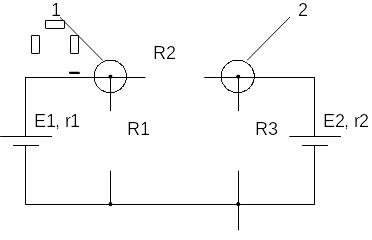
Решение: Два параллельно соединенных элемента образуют простейший делитель тока. Он состоит из двух ветвей. Так как нам дан реальный источник ЭДС для решения задачи представим его идеальным:
R2




r1
R1
R3
Е1


Найдем ток отдаваемый
источником в электрическую цепь
![]() .
Где
.
Где
![]() - общее сопротивление, которое находится
- общее сопротивление, которое находится
![]() .
Тогда
.
Тогда
![]() .
.
Свойство простейшего делителя тока: амплитуда тока в интересующей нас ветви делителя определяется амплитудой входного тока, умноженной на сопротивление другой ветви и деленной на сумму сопротивлений плеч делителя.
Зная ток отдаваемый
источнику можно рассчитать IR1
:
![]()
8. Для приведенной на рисунке схемы электрической цепи, пользуясь методом контурных токов, записать формулы, по которым рассчитываются элементы матрицы.
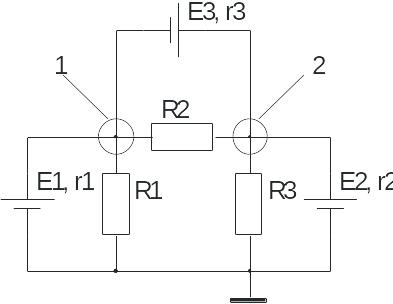
Р
r3
E3
R2
r1
Е1
R1
r2
Е2
R3
I
II
III
IV














Пользуясь методом контурных токов запишем матрицу
Z 11
Z12
Z13
Z14
11
Z12
Z13
Z14
Z21 Z22 Z23 Z24
Z31 Z32 Z33 Z34
Z41 Z42 Z43 Z44
Найдем формулы по которым рассчитывают элементы данной матрицы: Z11=R1+r1; Z22= R1+ R2+ R3; Z33= R2+ r3
Z44= R3+ r2; Z12= Z21=-R1; Z13= Z31=0; Z14= Z41=0;
Z23= Z32=- R2; Z24= Z42= R3; Z34= Z43=0.
9. Для приведенной на рисунке схемы электрической цепи, пользуясь методом узловых напряжений, записать формулы, по которым рассчитываются элементы матрицы.
Метод узловых
напряжений (МУН)
сводится к составлению и решению системы
уравнений только на основании первого
закона Кирхгофа. Количество уравнений,
которое приходится решать определяется
количеством узлов цепи без одного.
R1
R3
1
2
3

r2
R2
E2
E1
r1



4
Y 11
Y12 Y13 Y11=1/r1+1/R1;
11
Y12 Y13 Y11=1/r1+1/R1;
Y21 Y22 Y23 Y22=1/R1-1/R2+1/R3;
Y31 Y32 Y33 Y33=1/r2+1/R3;
Y12=Y21=-1/R1; Y13=0; Y23=Y32=-1/R3
10. Для приведенной на рисунке схемы электрической цепи рассчитать операторную передаточную характеристику. Для этой цепи построить ачх.
Передаточные характеристики RC - звеньев можно получить подстановкой в формулы величин операторных сопротивлений.
S=j![]()
Для этой схемы
операторные сопротивления равны
![]() и
и
![]() ,
,![]() .
Отсюда находим по правилу делителя
напряжения
.
Отсюда находим по правилу делителя
напряжения
![]()
![]()
Для АЧХ рассчитываем:
![]()
При ω
=
0
![]() K(ω)
= 1. При ω
= ∞
K(ω)
= 0
K(ω)
= 1. При ω
= ∞
K(ω)
= 0
1ц
К(w) АЧХ
АЧХ
w
S=j
Для этой схемы
операторные сопротивления равны
![]() ,
,![]() и
и
![]() .
Отсюда находим по правилу делителя
напряжения
.
Отсюда находим по правилу делителя
напряжения
![]()
![]()
Для АЧХ рассчитываем:
![]()
АЧХ
1ц
К(w)

w
Передаточные характеристики RL - звеньев также можно получить подстановкой в формулы величин операторных сопротивлений.
Для этой схемы
операторные сопротивления равны
![]() и
и
![]() .
При этом
.
При этом
![]() .
Отсюда находим
.
Отсюда находим
![]()
![]() ;
;
![]()
АЧХ
1ц
К(w)
w
Для этой схемы
операторные сопротивления равны
![]() и
и
![]() .
При этом
.
Отсюда находим
.
При этом
.
Отсюда находим
![]()
![]()
![]()
АЧХ
1ц
К(w)
w
11. Для периодической последовательности прямоугольных импульсов с заданными параметрами построить график амплитудно – частотного спектра Указать частоты, на которых располагаются дискретные компоненты спектра.
Вариант |
Амплитуда, В |
Частота следования |
Ед. изм. |
Длительность импульса |
Ед. изм |
1 |
0,016 |
4 |
кГц |
0,0625 |
мс |
2 |
0,32 |
80 |
МГц |
0,003125 |
мкс |
3 |
0,08 |
20 |
МГц |
0,0125 |
мкс |
4 |
2 |
400 |
МГц |
0,0005 |
мкс |
5 |
0,064 |
16 |
кГц |
0,015625 |
мс |
6 |
0,4 |
100 |
МГц |
0,0025 |
мкс |
Пример решения задания на варианте 1, остальные решайте сами по аналогии только с другими значениями.