
Московский государственный технический университет гражданской авиации
Кафедра ОРТЗИ
Контрольное домашнее задание по дисциплине «Исследование операций»
Тема: Определение оптимального интервала замены элементов радиотехнических систем с ростом вероятности отказов.
Выполнил: студент 3-го курса
группы. БИ 3-1
Колдаев М.А.
Преподаватель: Емельянов В.Е.
Москва 2010
Введение.
Характерной особенностью современного развития техники является широкое внедрение методов и средств автоматики и телемеханики, вызванное переходом на автоматизированное и автоматическое управление различными производственными и технологическими процессами, создание гибких производственных модулей, систем, комплексов и тому подобное. В условиях современной экономики автоматизация является одним из основных направлений технического прогресса. И, конечно, улучшение эффективности и качества проектируемых АСУ, САУ, ГПМ, ГПС и т.д. невозможно без повышения надежности технических средств управления (ТСУ). Таким образом, выше изложенное является первой причиной возрастания фактора надежности в современных условиях развития техники и, в частности, проектировании технических систем (ТС) различного назначения.
Второй причиной, требующей повышения надежности, является возрастание сложности ТС, аппаратуры их обслуживания, жесткости условий их эксплуатации и ответственности задач, которые на них возлагаются.
Недостаточная надежность ТС приводит к увеличению доли эксплуатационных затрат по сравнению с общими затратами на проектирование, производство и применение этих систем. При этом стоимость эксплуатации ТС может во много раз превзойти стоимость их разработки и изготовления. Кроме того, отказы ТС приводят различного рода последствиям: потерям информации, простоям сопряженных с ТС других устройств и систем, к авариям и т.д. Таким образом, третьей причиной повышения роли надежности в современных условиях является экономический фактор.
И, наконец, последнее. В конечном счете, надежность ТС определяется надежностью комплектующих элементов. Поэтому знание основных вопросов надежности элементной базы является необходимым условием успешной работы в области информатики и управления.
Анализ методов решения. Надежность радиоэлектронных систем при учете внезапных отказов.
Предположим, что радиоэлектронная система состоит из n элементов, вероятность безотказной работы которых задана. В качестве элемента могут быть блок, каскад, узел и т.д. Предположим так же, что элементы отказывают независимо друг от друга, т.е. отказ любого элемента или группы элементов не изменяет надежности других.
Рассмотрим в начале такую систему, в которой элементы соединены последовательно в смысле надежности, т.е. отказ одного из них вызывает отказ всей системы.
Причем будем полагать, что система отказывает только вследствие внезапных отказов.
Тогда для безотказной работы системы
в течении времени необходимо, чтобы
каждый элемент работал безотказно в
течении этого времени. Обозначим через
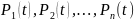 вероятность безотказной работы
соответственно n элементов
системы.
вероятность безотказной работы
соответственно n элементов
системы.
Так как элементы независимы в смысле надежности, то
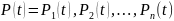 ,
(1.1)
,
(1.1)
А
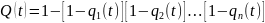 ,
(1.2)
,
(1.2)
Таким образом, при последовательном соединении элементов их вероятности их вероятности безотказной работы перемножаются. Выразим вероятности безотказной работы через интенсивность отказов
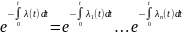
Откуда
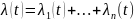 ,
(1.3)
,
(1.3)
Т.е. при последовательном соединении элементов их интенсивности отказов складываются. В частности, для экспоненциального закона, тогда
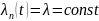
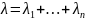
И
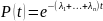 ,
(1.4)
,
(1.4)
Это означает, что надежность системы
также будет подчиняться экспоненциальному
закону. Если обозначить в этом случае
через
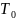 среднее время безотказной работы
системы, а через
среднее время безотказной работы
системы, а через
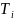 (i=1,2,…,n) –
среднее время безотказной работы i-ого
элемента, то
(i=1,2,…,n) –
среднее время безотказной работы i-ого
элемента, то
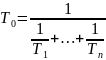 ,
(1.5)
,
(1.5)
В радиоэлектронной системе всегда могут
быть группы одинаковых элементов. Если
эти одинаковые элементы находятся в
примерно одинаковых условиях или
различие условий не влияет существенно
на их надежность. Предположим, что в
первый группе находится
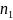 элементов с вероятностью безотказной
работы
элементов с вероятностью безотказной
работы
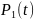 ,
то во второй группе
,
то во второй группе
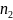 элементов с вероятностью безотказной
работы
элементов с вероятностью безотказной
работы
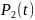 и т.д. Тогда формулы (10.1)-(10.5) запишутся
так:
и т.д. Тогда формулы (10.1)-(10.5) запишутся
так:
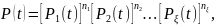
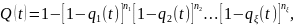 (1.6)
(1.6)
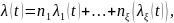
А в случае экспоненциальных законов в виде
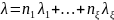
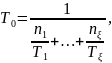
Где ξ – число групп элементов.
В частности, когда все элементы системы
имеют одинаковую надежность
 ,
то:
,
то:
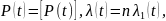 (1.7)
(1.7)
А для экспоненциального закона:
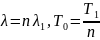 (1.8)
(1.8)
Рассмотрим теперь систему, к которой элементы соединены параллельно, т.е. отказ системы наступает только тогда, когда отказывают все входящие в систему элементы. Так как все элементы независимы в смысле надежности, то для такой системы получим, что
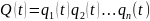 (1.9)
(1.9)
Т.е. при параллельном соединении элементов в системе их вероятности отказа перемножаются. В частности, когда все элементы равнонадежны, то получим
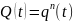 (1.10)
(1.10)
Если надежность каждого элемента подчиняется экспоненциальному закону, то надежность системы уже не будет подчиняться этому закону. Например для случая равных элементов
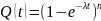 (1.11)
(1.11)
Для этого случая можно найти среднее время безотказной работы системы
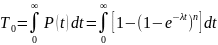 (1.12)
(1.12)
Сделаем замену
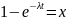
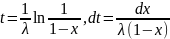
Тогда
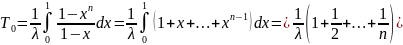
Таким образом,
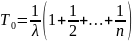 (1.13)
(1.13)
При большом n можно использовать следующее приближенное равенство:
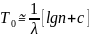 ,
где с=0,577 (1.14)
,
где с=0,577 (1.14)
При оценке надежности рассмотренных выше радиоэлектронных систем предполагалось, что элементы систем независимы в смысле надежности. Это допущение в реальных радиоэлектронных системах иногда может не выполняться. Так, например, могут быть случаи, когда отказы одних элементов, могут влиять на надежность других элементов, изменяя параметры , определяющие их надежность.
В случае параллельного соединения отказы одних элементов приводят к увеличению функциональной нагрузки на оставшиеся не отказавшие элементы и их надежность, естественно, уменьшается.
В общем случае задачи об определении надежности радиоэлектронных систем с зависимыми элементами не решена. Основная трудность при оценке надежности таких систем состоит в том, что не известны условные вероятности отказа одних элементов при условии отказа других, а опытное определение этих вероятностей требует необходимого объема экспериментов и вычислений.
