2.1.3. Оценка аннуитетов

Частный случай денежного потока, в котором денежные поступления в каждом периоде одина­ковы по величине, носит название аннуитета. Если число равных временных интервалов ограни­чено, аннуитет называется срочным. В этом случае

С1=С2=...=Сn=А.

Для оценки будущей и настоящей стоимости аннуитета можно пользоваться вышеприведенными формулами, вместе с тем благодаря специфике аннуитетов, заключающейся в равенстве денежных поступлений эти формулы могут быть существенно упрощены. Если в формулах настоящей и будущей стоимости денежного потока заменить на А и вынести этот множитель за знак суммы, то под знаком суммы останется сумма первых n членов геометрической прогрессии. Применив известную из алгебры формулу, можно получить следующие упрощенные формулы для оценки аннуитета:

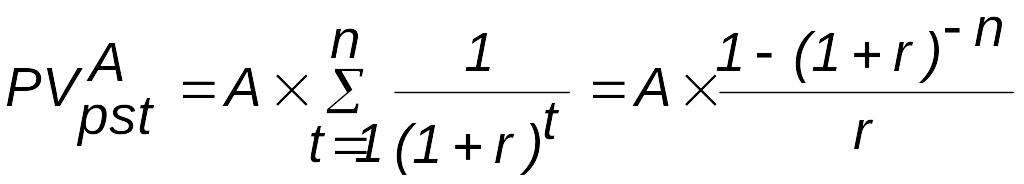(2.1.15)

(2.1.16)

(2.1.17)

(2.1.18)

Аннуитет называется бессрочным, если денеж­ные поступления продолжаются достаточно длительное время (в западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет).

Настоящая стоимость бессрочного аннуитета определяется с использованием формулы для расчета суммы членов бесконечной геометрической прогрессии:

PV = A / r (2.1.19)

Эта формула служит для оценки целесообразности приобретения бессрочного аннуитета. В данном случае известен размер годовых по­ступлений; в качестве ставки дисконтирования r обычно прини­мают гарантированную процентную ставку (например, процент, предлагаемый государственным банком).

2.2. Методы оценки финансовых активов

2.2.1. Внутренняя стоимость финансового актива

Финансовые активы – важнейший объект управления финансового менеджера. Финансовые активы обращаются на специально создаваемых рынках. Финансовый актив, рассмотренный как товар, характеризуется стоимостью, ценой, доходностью и риском. Именно эти характеристики лежат в основе управле­ния финансовыми активами, которое сводится к принятию решений кратко- и долгосрочного характера в отношении целесообразности их приобретения, прода­жи и сочетания при конструировании требуемых инструментов и операций. Знание существа указанных рыночных индикаторов, а также алгоритмов их расчета, является необходимым условием принятия эффективных финансовых решений.

Несмотря на складывающуюся на рынке вполне определенную текущую цену, любой финансо­вый актив может иметь разную степень привлекательности для потенциальных инвесторов и разную ценность.

Оценка ценности финансового актива с позиции определенного участника рынка определяет его внутреннюю стоимость.

Таким образом, каждый финансовый актив имеет столько оценок значений внутренней стоимости, сколько имеется инвесторов на рынке, заинтересованных в данном активе.

Цена (P) и внутренняя стоимость (V) – абсолютные величины, которые не только меняются в динамике, но, с позиции конкретного инвестора, нередко могут не совпадать. Различие цены и стоимости финансового актива проявляется в следующих моментах:

• стоимость – это расчетный показатель; цена – декларированный, т. е. объяв­ленный, который можно видеть в прейскурантах, котировках;

• в любой момент времени цена однозначна; стоимость многозначна, при этом число оценок стоимости зависит от числа профессиональных участников рынка;

• в условиях равновесного рынка цена, во-первых, количественно выражает внутренне присущую активу стоимость; во-вторых, стихийно устанавливается как среднее из оценок стоимости, рассчитываемых инвесторами.

Очевидно, в каждый данный момент возможны три ситуации:

1) P > V, 2) P < V, 3) P = V.

В первом случае приобретение данного финансового актива нецелесообразно. Если же в распоряжении финансового менеджера такие активы имеются, то их следует продать.

Во втором случае есть смысл купить финансовый актив.

Если имеет место третье соотношение, то спекулятивные операции теряют смысл.

Каждый участник рынка полагает, что он владеет более качественной информацией и методами ее обработки, чем другие участники, а потому может обоснованно оценить соответст­вие Р и V и принять соответствующее решение.