Методы анализа сетей Петри.

Дерево достижимости.

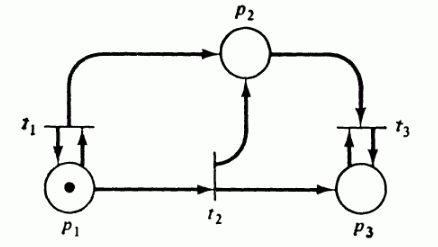
Рис 4.4: Маркированная сеть Петри, для которой строится дерево достижимости.

Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис. 4.4. Её начальная маркировка – (1, 0, 0). Это – корневая вершина дерева достижимости. Непосредственно достижимые из неё маркировки – это вершины второго уровня и т.д.

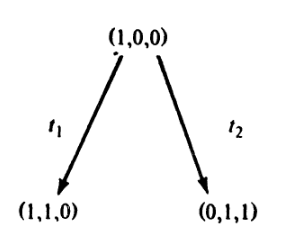
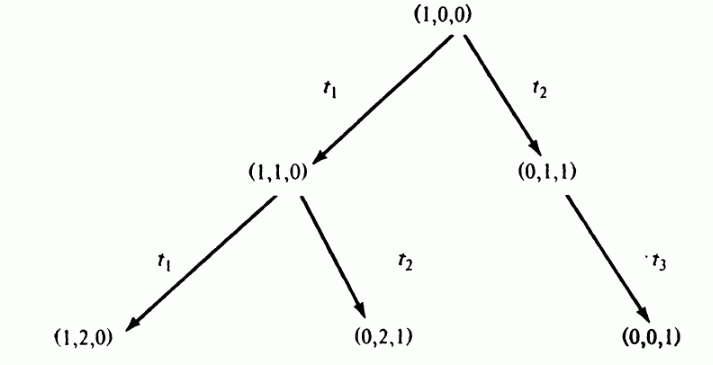
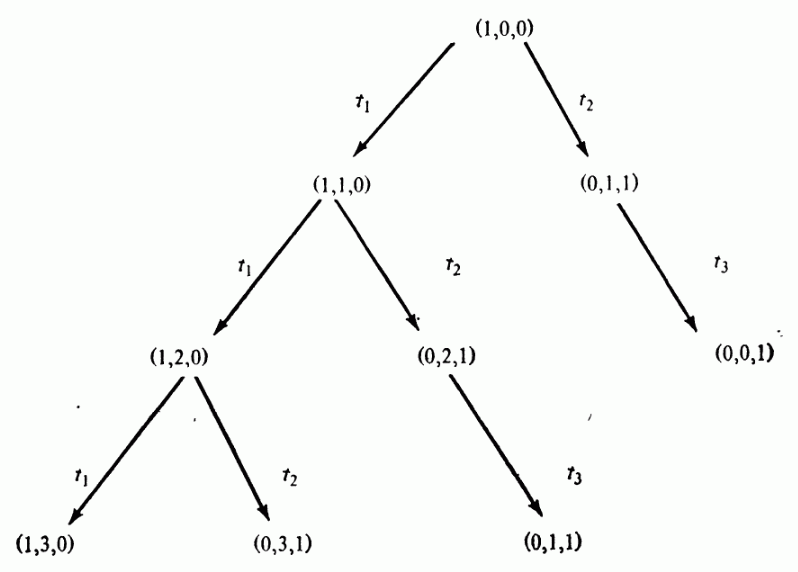
Рис 4.5: Первые три шага построения дерева достижимости для сети Петри на рис 4.4.

Получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево.

Пассивные маркировки – маркировки, в которых нет разрешенных переходов. Они называются терминальными вершинами. Другой класс маркировок – это маркировки, ранее встречавшиеся в дереве. Они называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды – все они будут порождены из места первого появления дублирующей маркировки в дереве. Таким образом, в дереве на рис.4.5 маркировка (0, 1, 1), получившаяся в результате выполнения последовательности 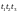, не будет порождать какие-либо новые вершины, поскольку она ранее встречалась в дереве в результате выполнения перехода 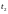из начальной маркировки.

Для сведения дерева достижимости к конечному представлению используется еще одно средство. Рассмотрим последовательность запусков переходов σ, начинающуюся в начальной маркировке  и кончающуюся в маркировке ' > ,. Маркировка ' совпадает с маркировкой , за исключением того, что имеет некоторые «дополнительные» фишки в некоторых позициях. Теперь, поскольку на запуски переходов лишние фишки не влияют, последовательность σ можно запустить снова, начиная в ' и приходя к маркировке ". В общем случае можно запустить последовательность σ n раз, получив в результате маркировку 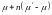. Следовательно, для тех позиций, которые увеличивают число фишек последовательностью σ, можно создать произвольно большое число фишек, просто повторяя последовательность σ столько, сколько это нужно. В сети Петри на рис. 4.4, например, можно запустить переход 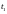столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в р₂. Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа ω, который обозначает «бесконечность». Для любого постоянного а определим

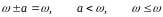. (4.5)

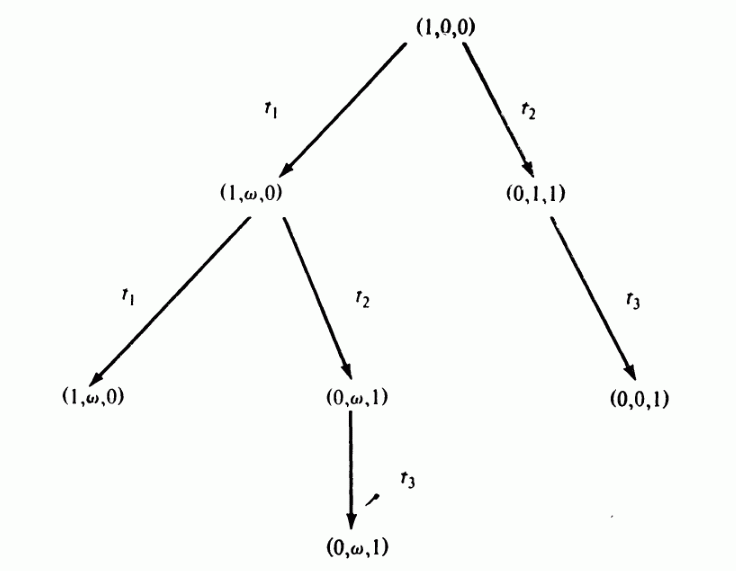
Рис 4.6: Дерево достижимости для сети Петри изображённой на рис 4.4.

Можно показать, что алгоритм построения дерева достижимости заканчивает работу.

Лекция 5. Анализ сетей Петри (продолжение).

Безопасность и ограниченность.

Сеть Петри ограниченна тогда и только тогда, когда символ 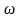отсутствует в ее дереве достижимости. Если сеть Петри ограниченна дерево достижимости будет содержать вершину, соответствующую всякой достижимой маркировке. Это позволяет решить вопросы анализа простым перебором и проверкой конечного множества всех достижимых маркировок. Например, чтобы определить границу для заданной позиции, нужно построить дерево достижимости и найти наибольшее значение компоненты маркировки, соответствующей этой позиции. Найденное значение является границей числа фишек для заданной позиции. Если граница для всех позиций равна 1, сеть безопасна.

Сохранение.

Если маркировка имеет в качестве маркировки некоторой позиции тогда для того, чтобы сеть была сохраняющей, вес этой позиции должен быть равным 0. Если сеть сохраняющая, существуют взвешенная сумма, обозначим её s, и вектор весов w = (w₁, w₂, .., w_n). Для каждой маркировки дерева достижимости имеем

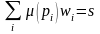. (5.1)

Если система (5.1) имеет решение, то сеть сохраняющая с весом.

Покрываемость.

Данная задача решается проверкой дерева достижимости. Строим для начальной маркировки дерево достижимости. Затем ищем любую вершину с " '. Если такой вершины не существует, маркировка ' не покрывается никакой достижимой маркировкой; если она найдена, то это и есть искомая маркировка. Путь от корня к покрывающей маркировке определяет последовательность переходов, которые приводят из начальной маркировки к покрывающей маркировке. Символ вновь должен рассматриваться как обозначение бесконечного множества значений. Если компонента покрывающей маркировки — , то в пути от корня к покрывающей маркировке имеется цикл. Для увеличения соответствующей компоненты с тем, чтобы она была не меньше, чем в данной маркировке, необходимо достаточное число раз повторить этот цикл.

Ограниченность дерева достижимости.

Дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, а также для определения возможной последовательности запусков. Решение этих задач ограничено существованием символа . Символ означает потерю информации; конкретные количества фишек отбрасываются, учитывается только существование их большого числа.