Решение линейных алгебраических уравнений в матричной форме

Маткад позволяет решать системы линейных алгебраических уравнений в матричной форме. Решение можно получить двумя способами.

1. Способ.

Система линейных алгебраических уравнений в матричной форме имеет вид:

AX=B, где

A – квадратная матрица коэффициентов,

X – вектор - столбец неизвестных,

B – вектор - столбец правых частей.

Решение системы в матричной форме : X= A^-1 B.

Решим в матричной форме систему

11x+12y+31z = 9

4x+52y+69z = 8

7x+86y+93z = 7

Для этого (см. рисунок 11):

1. Наберем ORIGIN:=1. Как говорилось выше, это означает, что счет элементов будет производиться не от нуля, а с единицы.

2. Введем матрицу А.

3. Введем вектор – столбец В.

4. Набор выражения для Х желательно выполнять, используя соответствующую кнопку матричной панели.

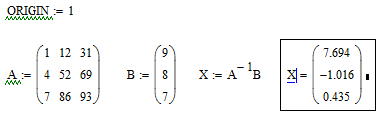5. После этого наберем X= и сразу получим вектор ответа.

Рис.11.Решение системы линейных уравнений в матричной форме

1. способ

Возможно получения решения матричного уравнения с помощью специальной функции lsolve, как показано на рис. 12.

Р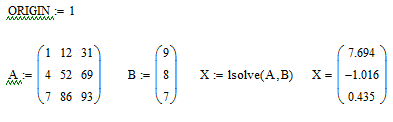 ис.12.Решение системы линейных алгебраических уравнений с использованием встроенной функции lsolve

Решить системы уравнений, представленные в таблице 5, матричным способом в соответствии с номером бригады.

Численное решение нелинейных алгебраических уравнений.

В Маткаде корни алгебраических уравнений и систем определяются с помощью следующих встроенных функций:

1. Функция root (expr, var) вычисляет действительное значение переменной var, при котором выражение expr равно нулю, т.е. она вычисляет один действительный корень уравнения. При этом необходимо задать его начальное приближение. Ниже приведен пример использования этой функции для нахождения действительного корня уравнения

x²+2x+1=0.

Р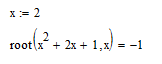 ис.13. Нахождение одного корня полинома.

2. Функция polyroots (v) позволяет вычислять все корни полинома.

Например, для решения уравнения

8х² + 2х + 3 = 0

набираем или считываем из таблицы функций (кнопка f(x)) функцию polyroots и в скобках заполняем вектор, вставляя коэффициенты уравнения. Нажимаем клавишу = и получаем ответ:

Р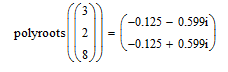 ис.14. Вычисление корней с помощью функции Polyroots.

Вычислить все корни многочленов, представленных в таблице 6, в соответствии с номером бригады.

Таблица 6

Номер бригады	Исходные многочлены
	5x5 +6x3 +8x2 +2x=0; 5x4 +8x3 +3x2 +9x+8=0; 4x4 +8x-3=0
	5x6 +6x5 +8x2 +2x=0; 15x4 +8x3 +31x2 +9x+8=0; 4x4 +8x2-3=0
	5x6 +6x5 +8x3 +2x=0; 25x4 +84x3 +3x2 +9x-8=0; 4x5 +8x2-3=0
	5x6 +6x4 +8x3 +20x=0; 2x4 +4x3 +3x2 +95x-8=0; 6x5 -8x3+4=0
	5x6 +6x4 +8x2 -10x=0; 12x4 +4x3 +3x2 +9x-81=0; 6x4 -8x3+4=0
	5x6 - 6x3 +8x2 -10x=0; x4 +4x3 +30x2 +9x-8=0; 6x5 -81x3+48=0
	5x5 - 6x4 +8x3+10x=0; 10x4 -40x3 +30x2 +9x-8=0; 6x4 -81x2+8=0
	5x5 - 6x3 +8x2+10x=0; 10x4 -4x3 +3x2 +9x-4=0; 6x4 -8x3+8=0
	5x5 + 6x4 +8x2+10x=0; 3x4 - x3 +3x2 +9x-4=0; 6x5 -81x2+8=0
	5x5 + 6x3 +8x2+10x=0; 3x4 - 15x3 +3x2 +29x-4=0; 6x5 -18x3+8=0