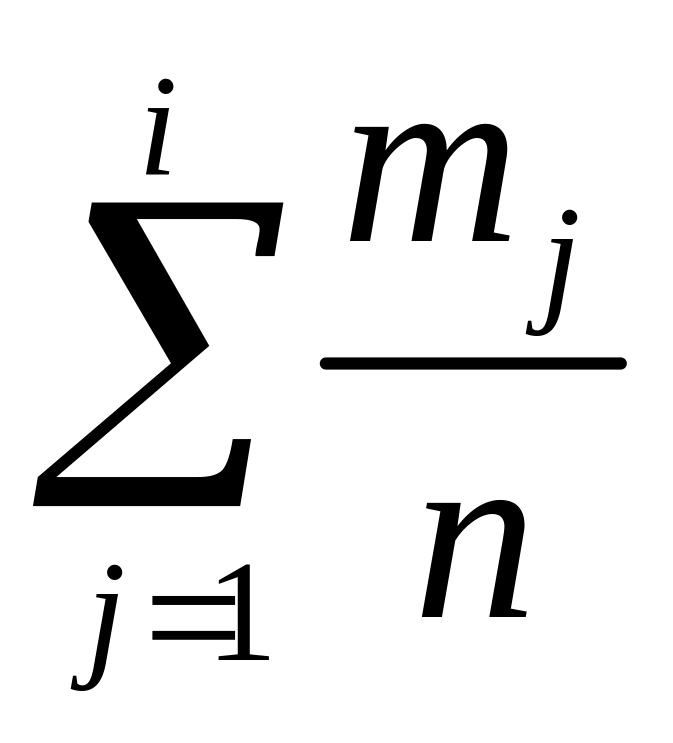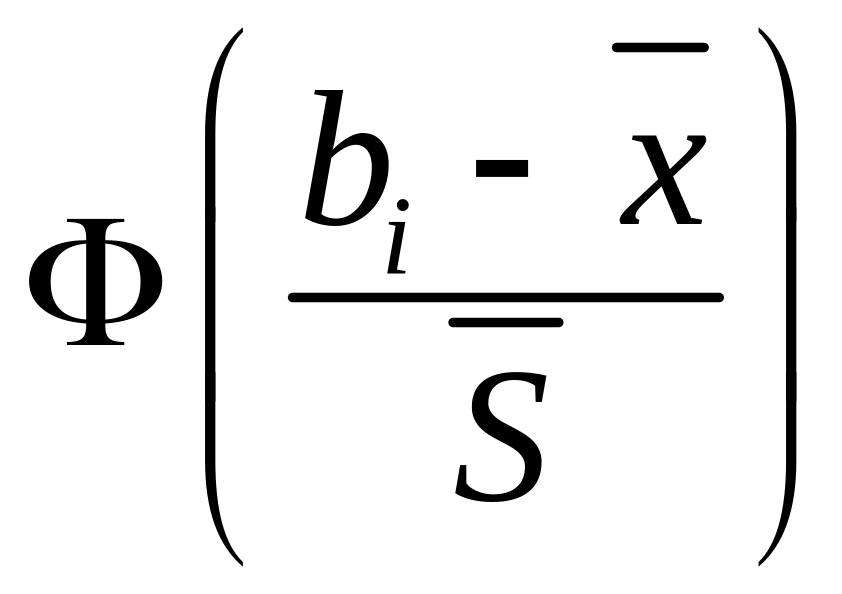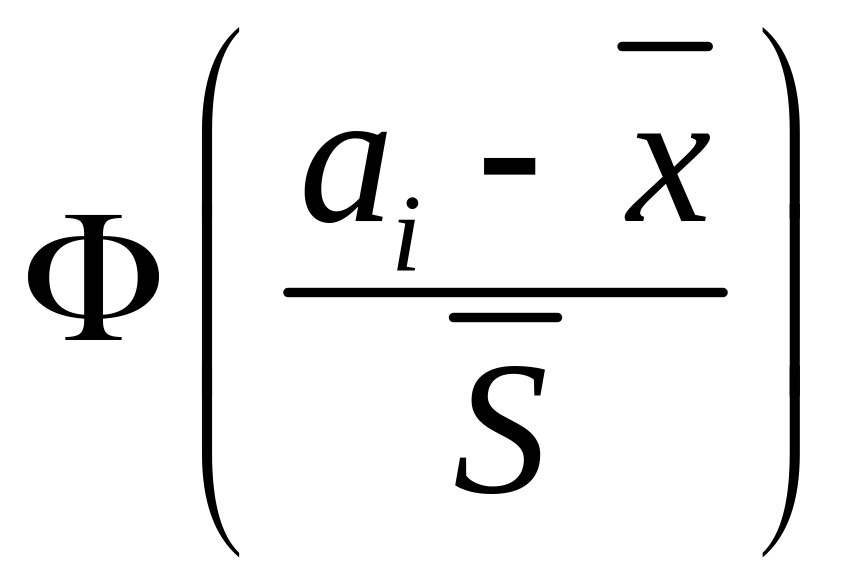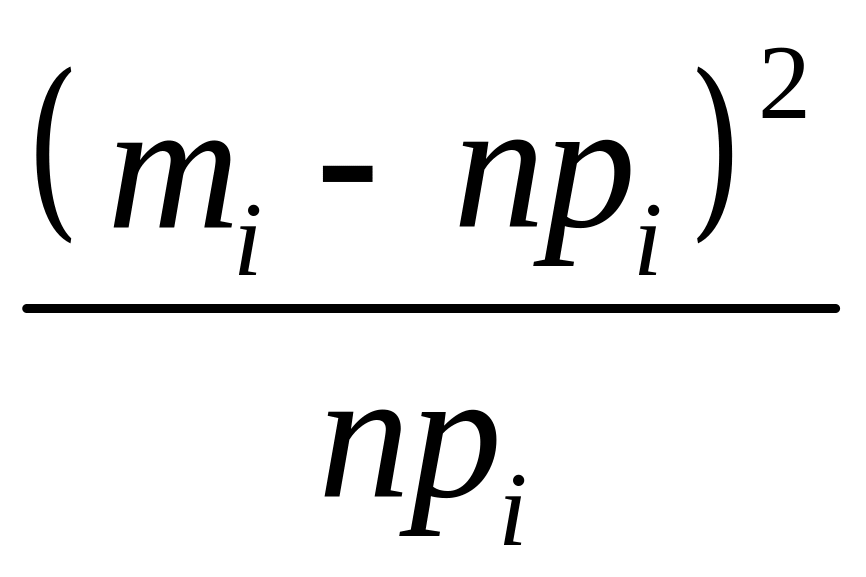- •Оглавление
- •Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •Рекомендуемая литература
- •Краткие теоретические сведения для выполнения контрольной работы № 1 и решение типовых задач
- •1.1. Матрицы и действия над ними
- •Действия над матрицами
- •1.2. Определители 2-го и 3-го порядков
- •Вычисление определителей 2-го и 3-го порядка
- •Свойства определителей
- •1.3. Обратная матрица
- •1.4. Решение систем линейных алгебраических уравнений (слаУр)
- •Матричный метод решения слаУр
- •Формулы Крамера для решения слаУр
- •Решить систему по формулам Крамера. Решение Формулы Крамера: . Вычислим определители:
- •Ранг матрицы
- •Рассмотрим матрицу специального вида
- •Метод Гаусса решения слаУр
- •Краткие теоретические сведения для выполнения контрольной работы № 2 и решение типовых задач
- •2.1. Прямая на плоскости
- •Условие параллельности двух прямых
- •Условие перпендикулярности двух прямых
- •2.2. Элементы векторной алгебры и аналитической геометрии в пространстве
- •Краткие теоретические сведения для выполнения контрольной работы № 3 и решение типовых задач
- •3.1. Раскрытие неопределенности вида .
- •3.2. Раскрытие неопределенности вида
- •3.3. Вычисление пределов с использованием второго замечательного предела
- •3.4. Непрерывность функции
- •Классификация точек разрыва
- •3.5. Правила дифференцирования
- •Правила дифференцирования
- •3.6. Производная сложной функции
- •3.7. Метод логарифмического дифференцирования
- •3.8. Производная функции, заданной неявно
- •3.9. Дифференцирование функций, заданных параметрически
- •- Параметр.
- •3.10. Исследование функций и построение графиков функций
- •Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
- •4.1. Метод интегрирования подведением под знак дифференциала
- •4.2. Метод интегрирования по частям
- •4.3. Интегрирование тригонометрических выражений
- •4.4. Вычисление площадей с помощью определенного интеграла
- •4.5. Несобственные интегралы 1-го рода
- •Краткие теоретические сведения для выполнения контрольной работы № 5 и решение типовых задач
- •5.1. Классическое определение вероятности
- •5.2. Формула полной вероятности
- •5.3. Формула Бернулли и ее следствия
- •Следствия формулы Бернулли
- •5.4. Дискретные случайные величины
- •Числовые характеристики дсв
- •5.5. Непрерывные случайные величины
- •Свойства функции распределения
- •Свойства плотности распределения
- •Числовые характеристики нсв
- •Краткие теоретические сведения для выполнения контрольной работы № 6 и решение типовых задач
- •6.1. Выборка из одномерной генеральной совокупности
- •Числовые характеристики выборки
- •Проверка статистической гипотезы о нормальном законе распределения генеральной совокупности с помощью критерия Пирсона
- •6.2. Выборка из двумерной генеральной совокупности
- •1. Элементы линейной алгебры
- •2. Элементы векторной алгебры и аналитической геометрии
- •3. Предел и производная функции одной переменной
- •4. Интегральное исчисление функции одной переменной
- •5. Теория вероятностей
- •6. Математическая статистика
- •Значения функции Лапласа
- •Сборник заданий по математике и статистике
- •191015, Г. Санкт-Петербург, ул. Кавалергардская, 7
Проверка статистической гипотезы о нормальном законе распределения генеральной совокупности с помощью критерия Пирсона
Постановка задачи. Относительно некоторой генеральной совокупности Х высказывается гипотеза Н (о возможных значениях числовых характеристик, о виде закона распределения…) которую называют статистической гипотезой. Из этой генеральной совокупности извлекается выборка . Требуется указать правило, при помощи которого можно было бы по каждой данной выборке решить вопрос о том, следует ли отклонить гипотезу Н или принять ее.
Нулевой
гипотезой
(основной) называют основную выдвигаемую
гипотезу
![]() .
.
Конкурирующей (альтернативной) называют гипотезу , которая противоречит нулевой гипотезе .
Для проверки нулевой гипотезы используют специально подобранную случайную величину, которая рассчитывается по экспериментальной выборке, точное или приближенное распределение которой известно. Эту случайную величину К называют статистическим критерием.
Зная
закон распределения К
можно определить вероятность попадания
К
в любой интервал, т.е.
![]() для любых значений а
и b.
для любых значений а
и b.
Обозначим:
![]() .
.
Уровнем значимости
называют условное достаточно малое
значение вероятности
![]() ,
соответствующее практически невозможному
событию
,
соответствующее практически невозможному
событию
![]() .
При этом область
.
При этом область
![]() называют критической
областью.
называют критической
областью.
Областью допустимых
значений
считают область
![]() ,
так как
,
так как
![]() достаточно велика при малых .
достаточно велика при малых .
Итак: при выбранном
значении
для данной гипотезы
известна критическая область
![]() ,
в которую с вероятностью
,
в которую с вероятностью
![]() критерий К
попасть не должен.
критерий К
попасть не должен.
Если вычисленный по выборке критерий К оказался в критической области , говорят о несоответствии гипотезы фактическим данным, т.е. об отсутствии оснований принять гипотезу . Если критерий К оказался вне критической области , говорят о соответствии гипотезы фактическим данным, т.е об отсутствии оснований отвергать гипотезу .
При статистической проверке правильности выдвигаемой гипотезы могут быть допущены ошибки двух родов: ошибка первого рода состоит в том, что гипотеза отвергнута, а она верна; ошибка второго рода состоит в том, что гипотеза принята, а она не верна.
Критерием согласия называют критерий проверки статистической гипотезы о предполагаемом законе неизвестного распределения СВ.
Критерий согласия Пирсона (критерий ).
Пусть выдвигается простая гипотеза , полностью определяющая вид функции распределения исследуемой СВ Х. При этом имеется выборка достаточно большого объема, которой соответствует определенный статистический ряд.
В качестве критерия проверки справедливости гипотезы выбирается СВ:
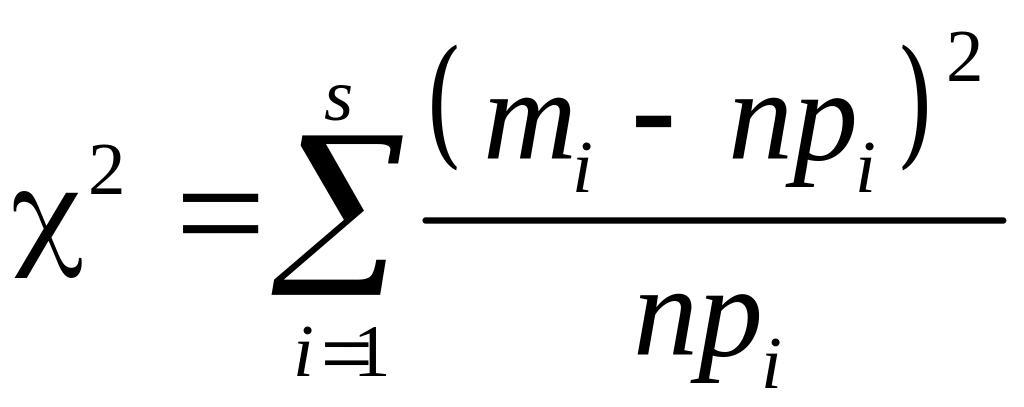 ,
,
где
– теоретические относительные частоты
появления величины
,
вычисленные в предположении гипотезы
по известной плотности распределения
вероятностей
;
![]() – теоретические абсолютные частоты
появления
.
– теоретические абсолютные частоты
появления
.
Эта
величина при
![]() распределена по закону
с
r
степенями свободы
распределена по закону
с
r
степенями свободы
![]() ,
,
где s – число различных значений СВ Х (количество интервалов группированной выборки), l – число параметров предполагаемого закона распределения.
Распределение
не
обладает симметрией, поэтому критическая
область выбирается односторонней
![]() ,
значение
,
значение
![]() полностью определяются по уровню
значимости
и данному значению
полностью определяются по уровню
значимости
и данному значению
![]() по таблице распределения
(приложение 2).
по таблице распределения
(приложение 2).
Критерий
использует тот факт, что случайная
величина
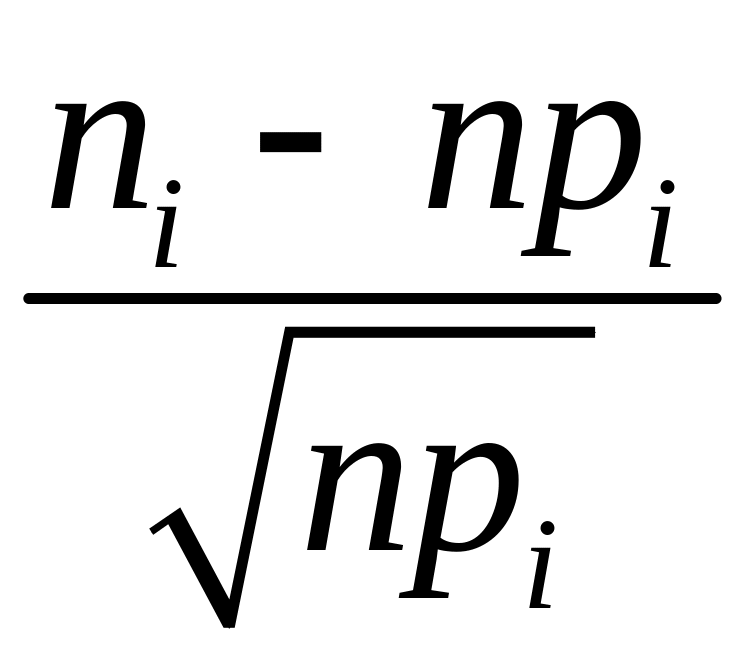 имеет распределение, близкое к нормальному
имеет распределение, близкое к нормальному
![]() .
Чтобы это утверждение было достаточно
точным, необходимо, чтобы для всех
интервалов группированного статистического
ряда выполнялось условие
.
Чтобы это утверждение было достаточно
точным, необходимо, чтобы для всех
интервалов группированного статистического
ряда выполнялось условие
![]() .
Если в некоторых интервалах это условие
не выполняется, то их следует объединять
с соседними. Так как после объединения
остается меньше интервалов, то число
степеней свободы следует вычислять,
используя число вновь полученных
интервалов.
.
Если в некоторых интервалах это условие
не выполняется, то их следует объединять
с соседними. Так как после объединения
остается меньше интервалов, то число
степеней свободы следует вычислять,
используя число вновь полученных
интервалов.
Пример
Результаты измерений некоторой физической величины представлены в таблице:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1;3,5 |
3,5;6 |
6;8,5 |
8,5;11 |
11;13,5 |
13,5;16 |
16;18,5 |
|
3 |
8 |
14 |
27 |
20 |
16 |
7 |
5 |
1. Найти функцию распределения выборки и построить ее график.
2. Построить гистограмму относительных частот.
3. Найти числовые характеристики выборки: выборочное среднее и исправленную выборочную дисперсию .
4. Используя функцию
Лапласа, построить доверительный
интервал для математического ожидания,
соответствующий доверительной вероятности
![]() .
.
5. С помощью критерия (Пирсона) проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости .
Решение
Объем выборки
,
длина интервала
![]() .
Для нахождения эмпирической функции
распределения
,
построения гистограммы относительных
частот и вычисления числовых характеристик
выборки дополним заданную таблицу
следующими строками: строкой, в которой
расположим средние точки
каждого интервала, строкой относительных
частот
,
строкой накопленных относительных
частот
.
Для нахождения эмпирической функции
распределения
,
построения гистограммы относительных
частот и вычисления числовых характеристик
выборки дополним заданную таблицу
следующими строками: строкой, в которой
расположим средние точки
каждого интервала, строкой относительных
частот
,
строкой накопленных относительных
частот
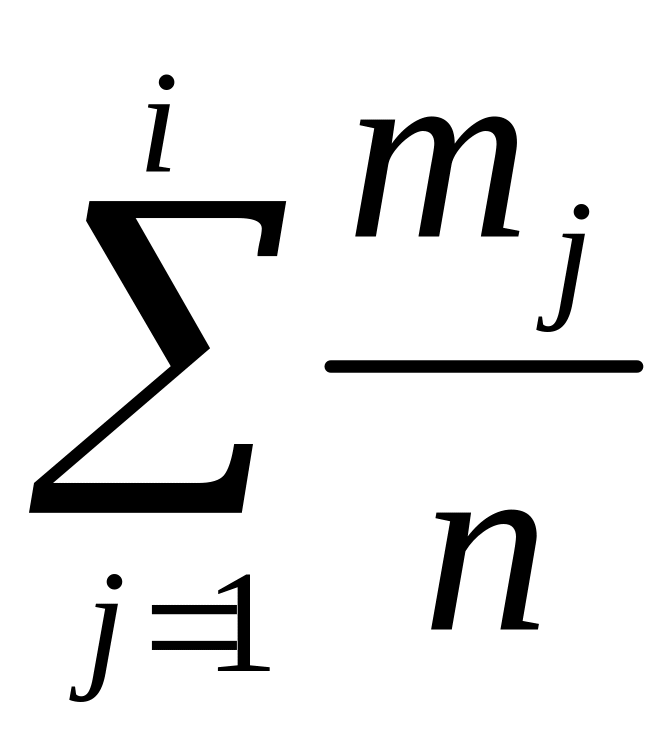 и строкой, в которой вычислим высоты
столбиков гистограммы относительных
частот
и строкой, в которой вычислим высоты
столбиков гистограммы относительных
частот
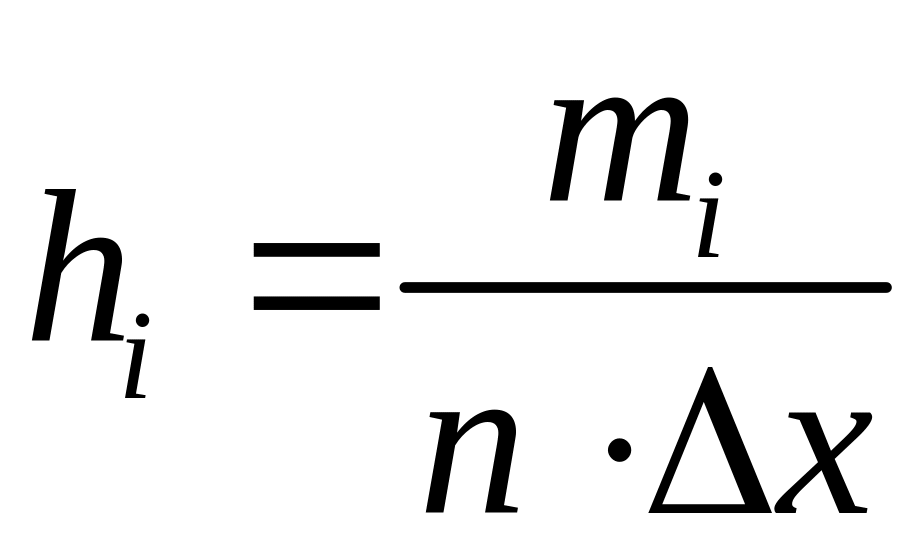 .
.
Таблица 1
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1;3,5 |
3,5;6 |
6;8,5 |
8,5;11 |
11;13,5 |
13,5;16 |
16;18,5 |
|
3 |
8 |
14 |
27 |
20 |
16 |
7 |
5 |
|
|
2,25 |
4,75 |
7,25 |
9,75 |
12,25 |
14,75 |
17,25 |
|
0,03 |
0,08 |
0,14 |
0,27 |
0,2 |
0,16 |
0,07 |
0,05 |
|
0,03 |
0,11 |
0,25 |
0,52 |
0,72 |
0,88 |
0,95 |
1 |
|
0,012 |
0,032 |
0,056 |
0,108 |
0,08 |
0,064 |
0,028 |
0,02 |
1. Эмпирическая функция распределения определяется по значениям накопленных относительных частот, которые расположены в шестой строке таблицы 1. Эта функция имеет скачки в точках – серединах интервалов группированного статистического ряда.
Аналитическое выражение эмпирической функции распределения имеет вид:
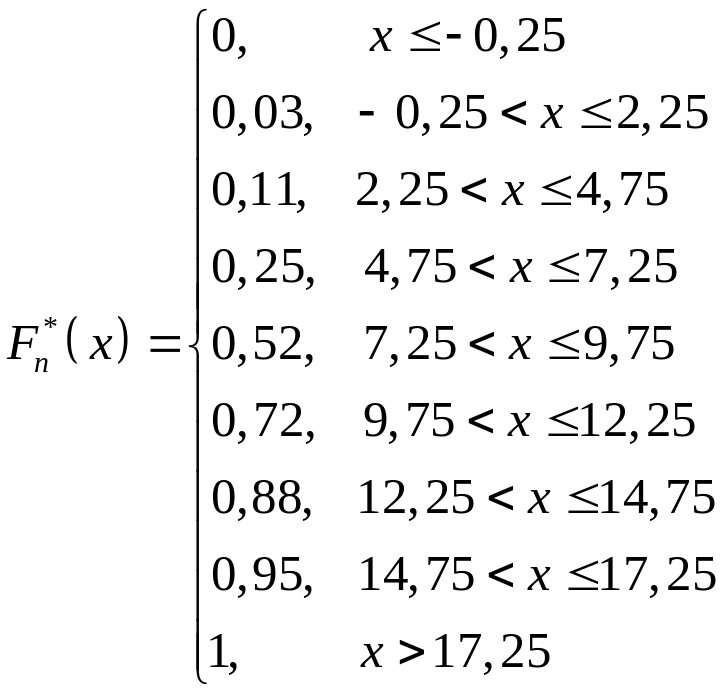 .
.
График эмпирической функции распределения изображен на рис. 1.
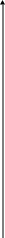
0,88
0,72
0,52
0,25
0,11
0,03














 1
1 0,95
0,95
Рис. 1
2. Построим гистограмму относительных частот, для этого на каждом интервале группированной выборки строим столбики, высоты которых вычислены в седьмой строке таблицы 1. График гистограммы изображен на рис. 2.
0





0,108


 0,08
0,08
 0,064
0,064

0,032 0,028


0,02

 0,012
0,012



Рис. 2
3. Найдем числовые характеристики выборки. Выборочное среднее находим по формуле , в нашем случае
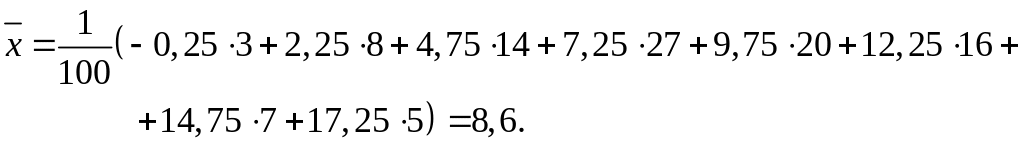
Исправленную выборочную дисперсию находим по формуле , в нашем случае
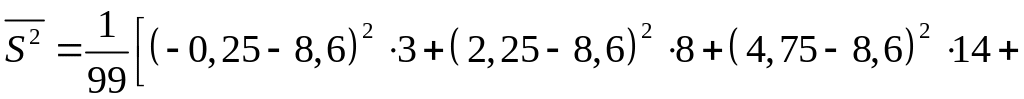
![]()
![]() .
.
4. При большом объеме выборки доверительный интервал для математического ожидания имеет вид
.
Используя таблицу
значений функции Лапласа (приложение
1) находим
![]() .
.
Вычислим
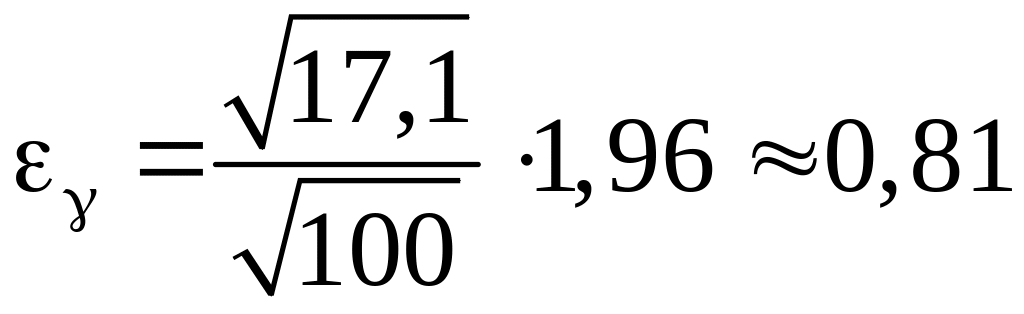 ,
тогда доверительный интервал для
математического ожидания имеет вид
,
тогда доверительный интервал для
математического ожидания имеет вид
![]()
или
![]() .
.
5. Выдвигаем простую гипотезу о нормальном распределении генеральной совокупности. В качестве критерия проверки справедливости гипотезы выбирается случайная величина
,
где находятся по формуле вероятности попадания случайной величины в интервал в предположении гипотезы о нормальном законе
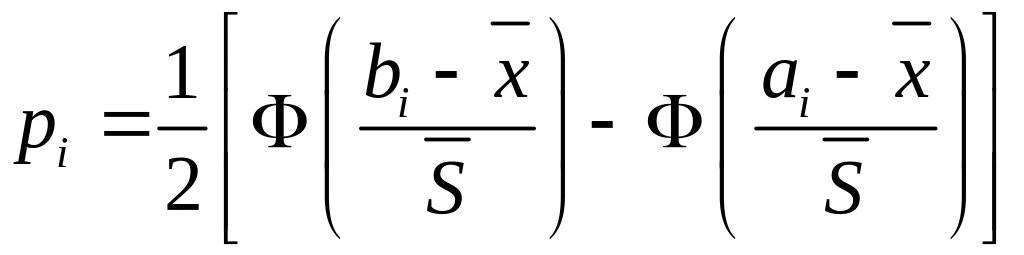 ,
,
где – функция Лапласа.
Замечание. Если
использовать таблицу значений функции
Лапласа
,
то вероятности попадания случайной
величины в интервал в предположении
гипотезы о нормальном законе распределения
находится по формуле
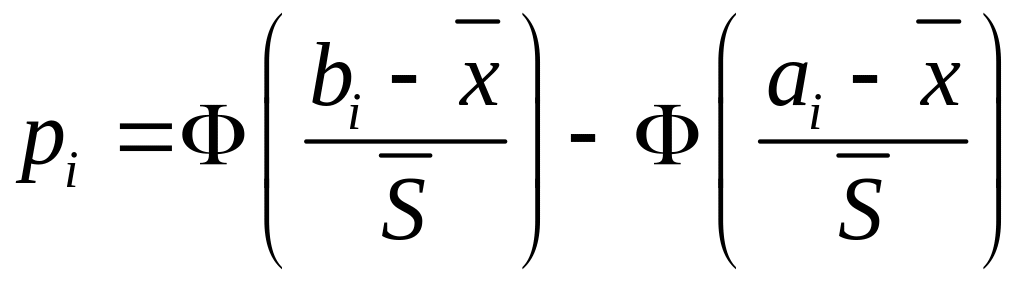 .
.
Для
соблюдения условия
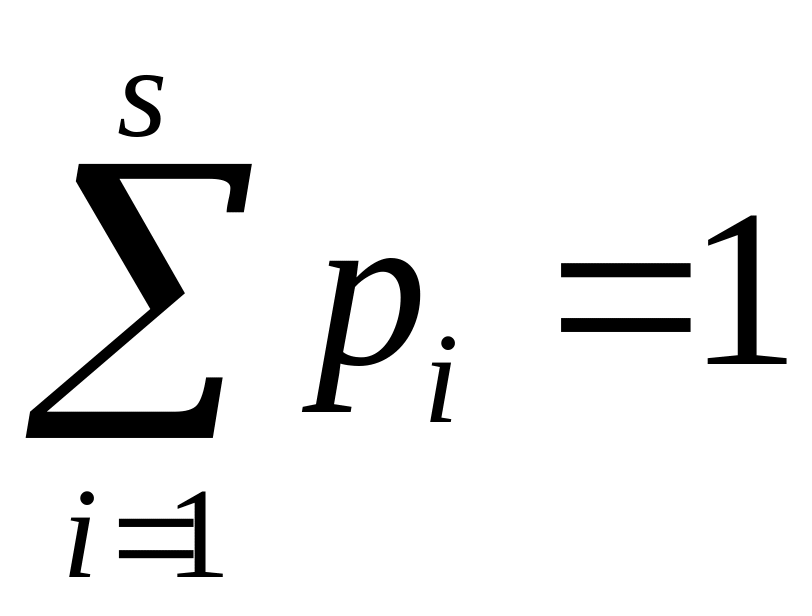 полагают
полагают
![]() ,
,
![]() .
.
Для вычисления критерия составим расчетную таблицу:
Таблица 2
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1;3,5 |
3,5;6 |
6;8,5 |
8,5;11 |
11;13,5 |
13,5;16 |
16;18,5 |
|
3 |
8 |
14 |
27 |
20 |
16 |
7 |
5 |
|
|
2,25 |
4,75 |
7,25 |
9,75 |
12,25 |
14,75 |
17,25 |
|
1 |
3,5 |
6 |
8,5 |
11 |
13,5 |
16 |
|
|
|
1 |
3,5 |
6 |
8,5 |
11 |
13,5 |
16 |
|
|
|
|
|
0,5803 |
1,1849 |
1,7895 |
|
|
|
|
|
|
|
0,5803 |
1,1849 |
1,7895 |
|
|
|
|
|
0,438 |
0,764 |
0,926 |
1 |
|
|
|
|
|
|
0,438 |
0,764 |
0,926 |
|
0,033 |
0,0755 |
0,1565 |
0,2255 |
0,2285 |
0,163 |
0,081 |
0,037 |
|
3,3 |
7,55 |
15,65 |
22,55 |
22,85 |
16,3 |
8,1 |
3,7 |
|
|
10,85 |
15,65 |
22,55 |
22,85 |
16,3 |
11,8 |
|
|
|
0,15 |
|
4,45 |
|
|
0,2 |
|
|
|
0,0225 |
2,7225 |
19,8025 |
8,1225 |
0,09 |
0,04 |
|
|
|
0,0020 |
0,1739 |
0,8781 |
0,3554 |
0,0055 |
0,0033 |
|
Находим сумму
элементов 11-ой и 12-ой строк таблицы 2,
получаем
 .
.
Критерий равен сумме элементов последней строки таблицы 12:
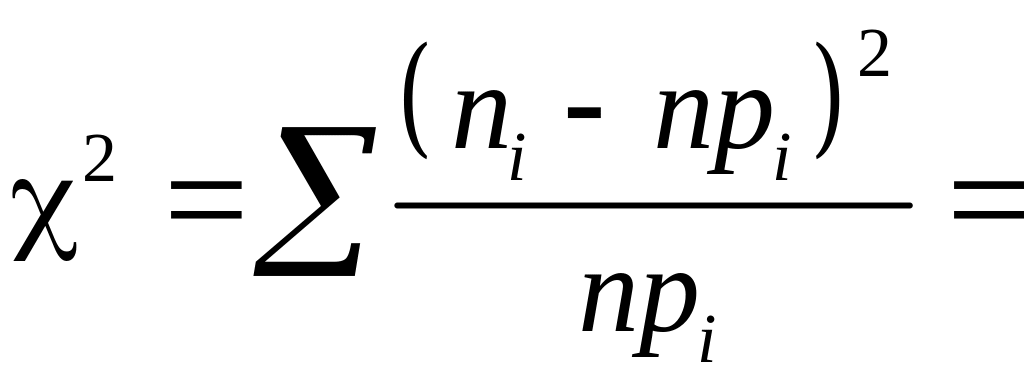
![]() .
.
Находим критическую
область
![]() .
Так как уровень значимости
по условию, число степеней свободы
.
Так как уровень значимости
по условию, число степеней свободы
![]() ,
то согласно таблице распределения
-
,
то согласно таблице распределения
-
![]() ,
критическая область имеет вид
,
критическая область имеет вид
![]() .
.
Так как критерий
![]() не попал в критическую область
не попал в критическую область
![]() ,
то нет оснований отвергать гипотезу о
нормальном законе распределения
генеральной совокупности.
,
то нет оснований отвергать гипотезу о
нормальном законе распределения
генеральной совокупности.