
- •Оглавление
- •Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •Рекомендуемая литература
- •Краткие теоретические сведения для выполнения контрольной работы № 1 и решение типовых задач
- •1.1. Матрицы и действия над ними
- •Действия над матрицами
- •1.2. Определители 2-го и 3-го порядков
- •Вычисление определителей 2-го и 3-го порядка
- •Свойства определителей
- •1.3. Обратная матрица
- •1.4. Решение систем линейных алгебраических уравнений (слаУр)
- •Матричный метод решения слаУр
- •Формулы Крамера для решения слаУр
- •Решить систему по формулам Крамера. Решение Формулы Крамера: . Вычислим определители:
- •Ранг матрицы
- •Рассмотрим матрицу специального вида
- •Метод Гаусса решения слаУр
- •Краткие теоретические сведения для выполнения контрольной работы № 2 и решение типовых задач
- •2.1. Прямая на плоскости
- •Условие параллельности двух прямых
- •Условие перпендикулярности двух прямых
- •2.2. Элементы векторной алгебры и аналитической геометрии в пространстве
- •Краткие теоретические сведения для выполнения контрольной работы № 3 и решение типовых задач
- •3.1. Раскрытие неопределенности вида .
- •3.2. Раскрытие неопределенности вида
- •3.3. Вычисление пределов с использованием второго замечательного предела
- •3.4. Непрерывность функции
- •Классификация точек разрыва
- •3.5. Правила дифференцирования
- •Правила дифференцирования
- •3.6. Производная сложной функции
- •3.7. Метод логарифмического дифференцирования
- •3.8. Производная функции, заданной неявно
- •3.9. Дифференцирование функций, заданных параметрически
- •- Параметр.
- •3.10. Исследование функций и построение графиков функций
- •Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
- •4.1. Метод интегрирования подведением под знак дифференциала
- •4.2. Метод интегрирования по частям
- •4.3. Интегрирование тригонометрических выражений
- •4.4. Вычисление площадей с помощью определенного интеграла
- •4.5. Несобственные интегралы 1-го рода
- •Краткие теоретические сведения для выполнения контрольной работы № 5 и решение типовых задач
- •5.1. Классическое определение вероятности
- •5.2. Формула полной вероятности
- •5.3. Формула Бернулли и ее следствия
- •Следствия формулы Бернулли
- •5.4. Дискретные случайные величины
- •Числовые характеристики дсв
- •5.5. Непрерывные случайные величины
- •Свойства функции распределения
- •Свойства плотности распределения
- •Числовые характеристики нсв
- •Краткие теоретические сведения для выполнения контрольной работы № 6 и решение типовых задач
- •6.1. Выборка из одномерной генеральной совокупности
- •Числовые характеристики выборки
- •Проверка статистической гипотезы о нормальном законе распределения генеральной совокупности с помощью критерия Пирсона
- •6.2. Выборка из двумерной генеральной совокупности
- •1. Элементы линейной алгебры
- •2. Элементы векторной алгебры и аналитической геометрии
- •3. Предел и производная функции одной переменной
- •4. Интегральное исчисление функции одной переменной
- •5. Теория вероятностей
- •6. Математическая статистика
- •Значения функции Лапласа
- •Сборник заданий по математике и статистике
- •191015, Г. Санкт-Петербург, ул. Кавалергардская, 7
5.5. Непрерывные случайные величины
Непрерывная СВ (НСВ) – это величина, множество возможных значений которой – непрерывное множество, т.е. сплошь заполняет некоторый промежуток (определение не строгое). Можно показать, что вероятность отдельного значения НСВ равна нулю. Из этого не следует, что событие невозможное. Это означает, что при неограниченном повторении опыта это событие будет появляться сколь угодно редко.
Универсальным законом распределения, пригодным как для ДСВ, так и для НСВ, который полностью характеризует СВ с вероятностной точки зрения, является функция распределения .
Свойства функции распределения
Функция распределения
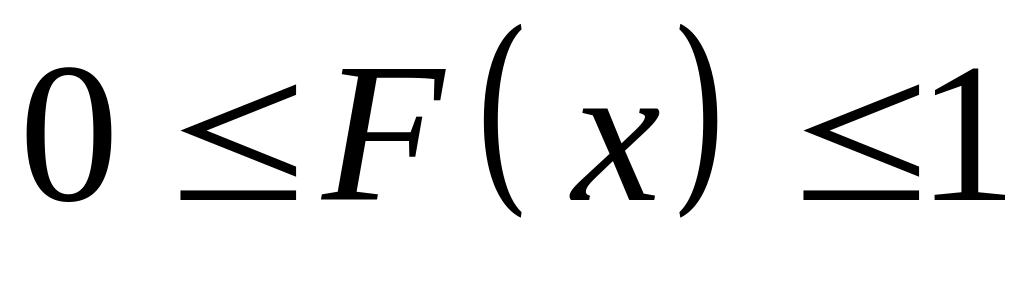 ,
что следует из определения функции
распределения, как вероятности события
,
что следует из определения функции
распределения, как вероятности события
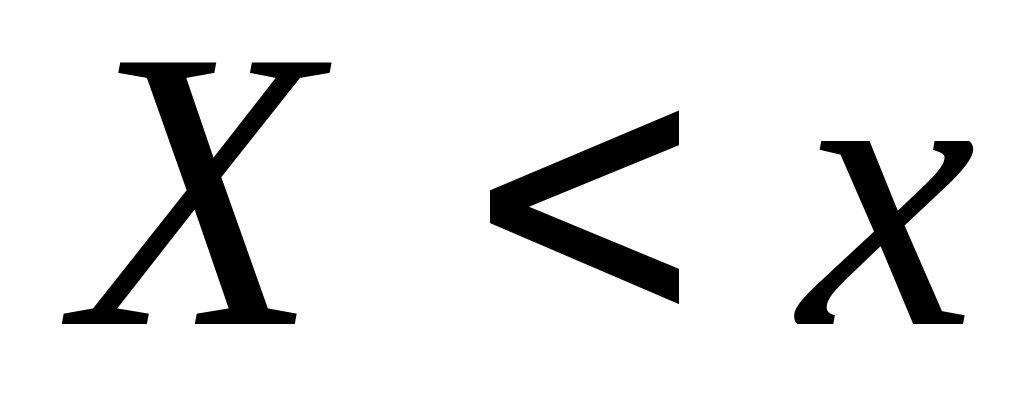 ,
а вероятность любого события
,
а вероятность любого события
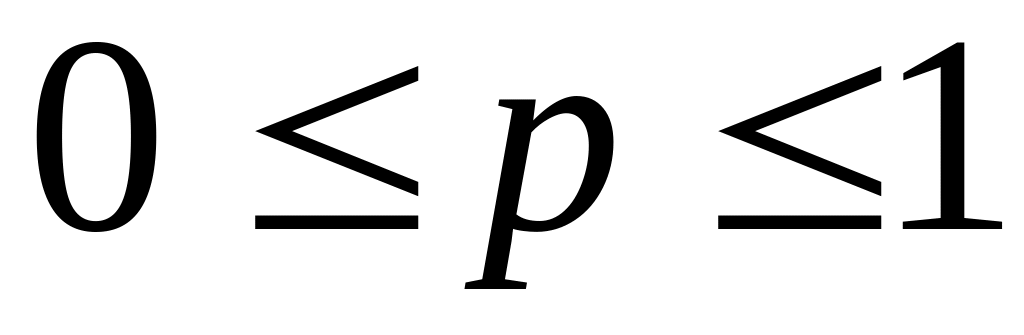 .
.Функция распределения неубывающая функция своего аргумента, т.е. если
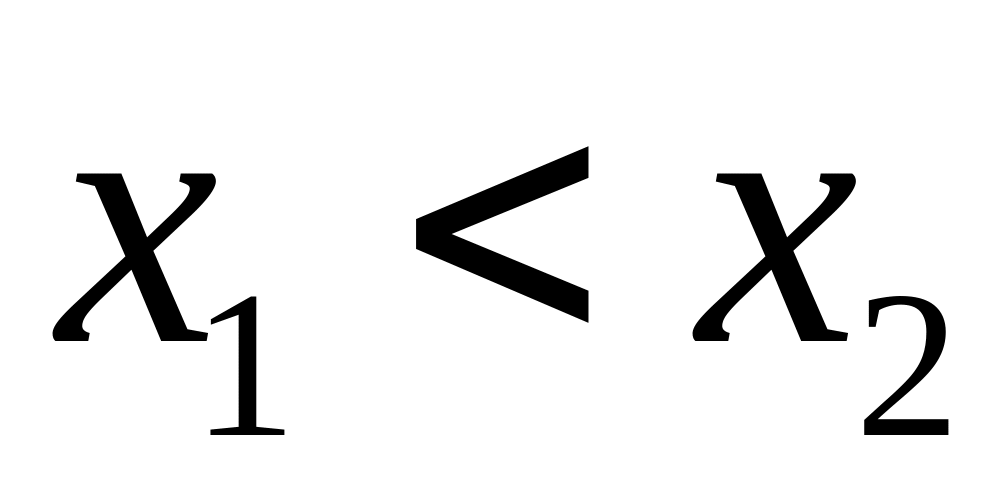 ,
то
,
то
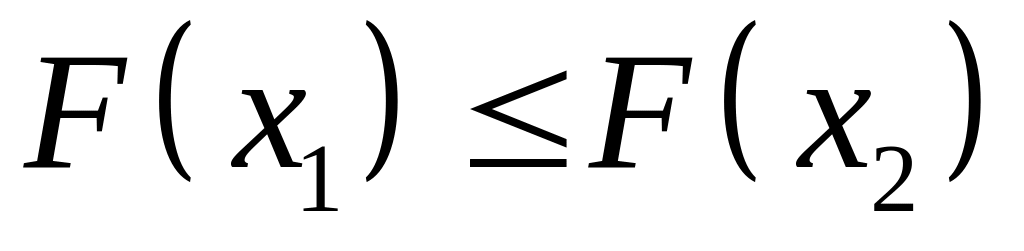 .
.Вероятность попадания СВ в промежуток
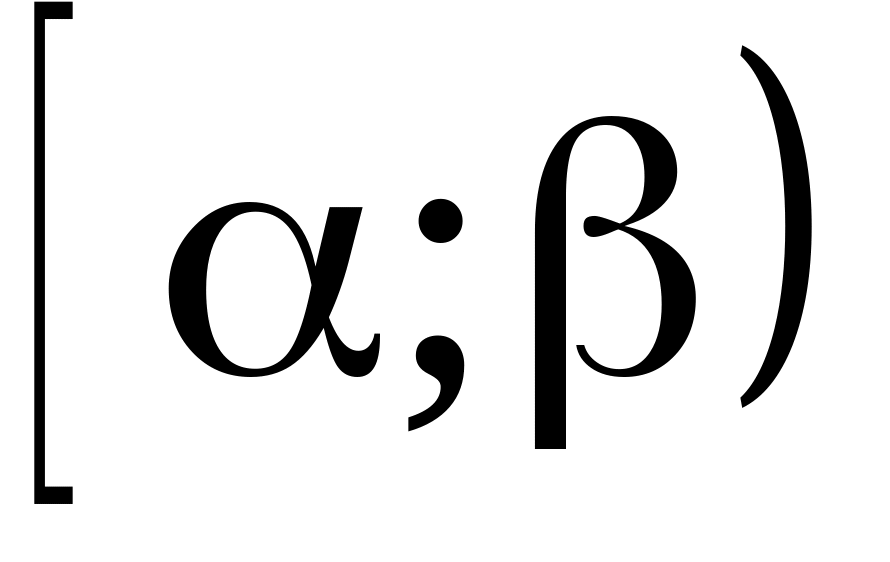 равна приращению функции распределения
на этом интервале
равна приращению функции распределения
на этом интервале
![]() .
.
Если возможные значения СВ принадлежат интервалу
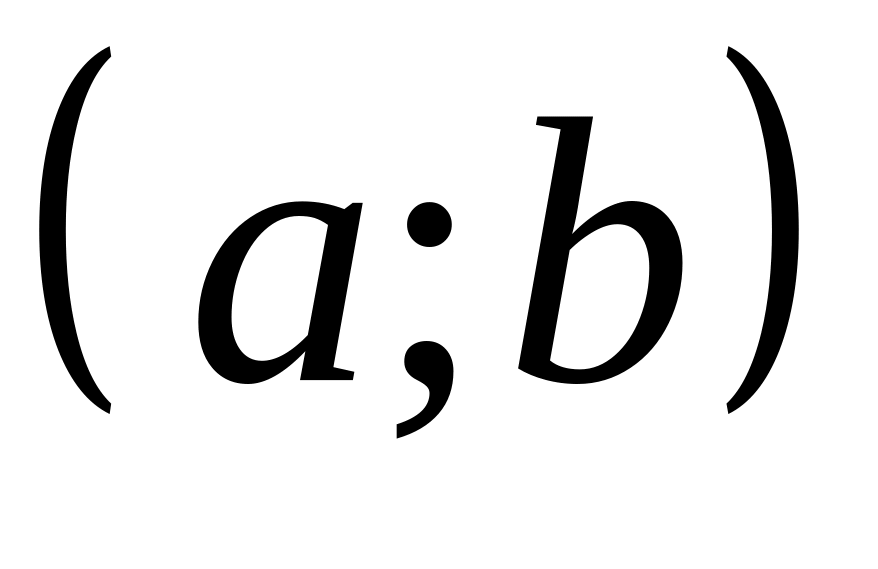 ,
то
,
то
1)
![]() при
при
![]() ,
2)
,
2)
![]() при
при
![]() .
.
Если возможные значения НСВ расположены на всей оси Ох, то
![]() ,
,
![]() .
.
Функция непрерывна слева, т.е.
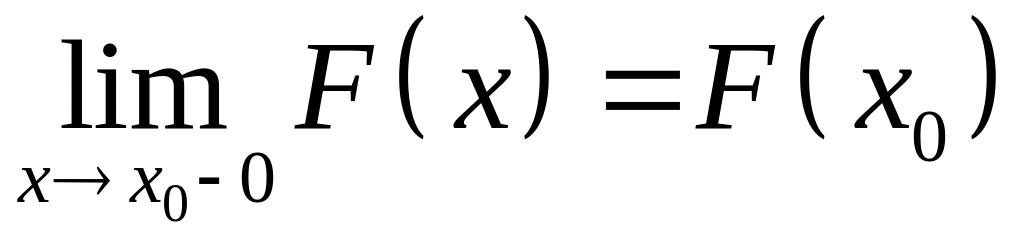 .
Для непрерывной СВ функция распределения
непрерывна всюду.
.
Для непрерывной СВ функция распределения
непрерывна всюду.
Замечание. Так как вероятность каждого отдельного значения НСВ равна нулю, то для НСВ справедливы равенства
![]() .
.
Плотностью распределения (или плотностью вероятности, или плотностью) НСВ Х в точке х называется производная ее функции распределения в этой точке:
![]() .
.
График плотности распределения называется кривой распределения. Плотность распределения существует только для НСВ.
Плотность распределения называют дифференциальной функцией распределения или дифференциальным законом распределения.
Свойства плотности распределения
Плотность распределения – неотрицательная функция, т.е.
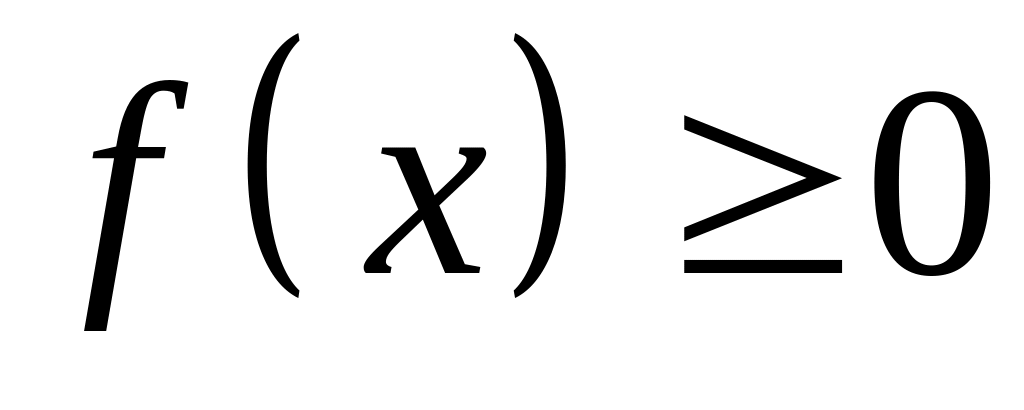 .
.
Вероятность попадания СВ с плотностью распределения в данный интервал
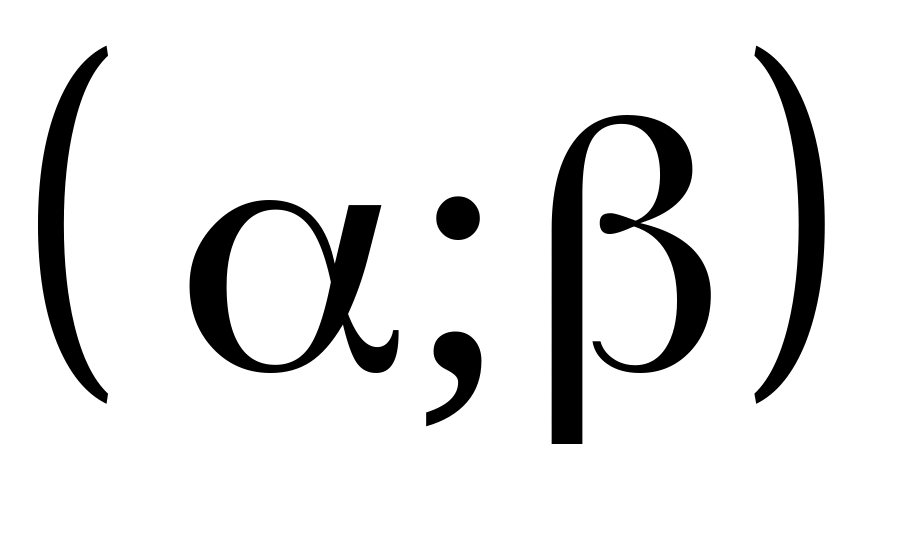 выражается формулой:
выражается формулой:
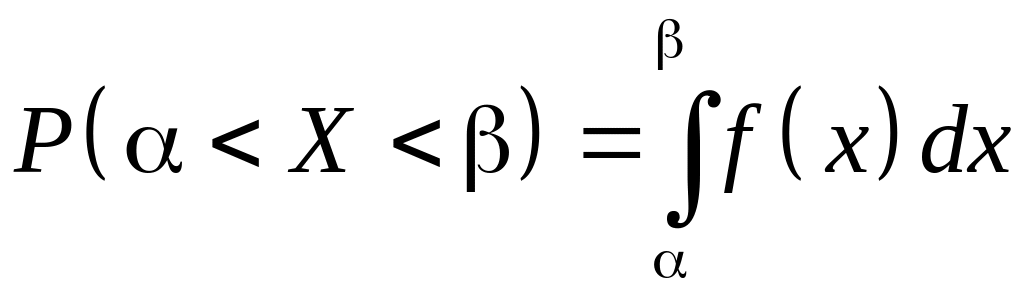 .
.
Функция распределения выражается через плотность распределения формулой:
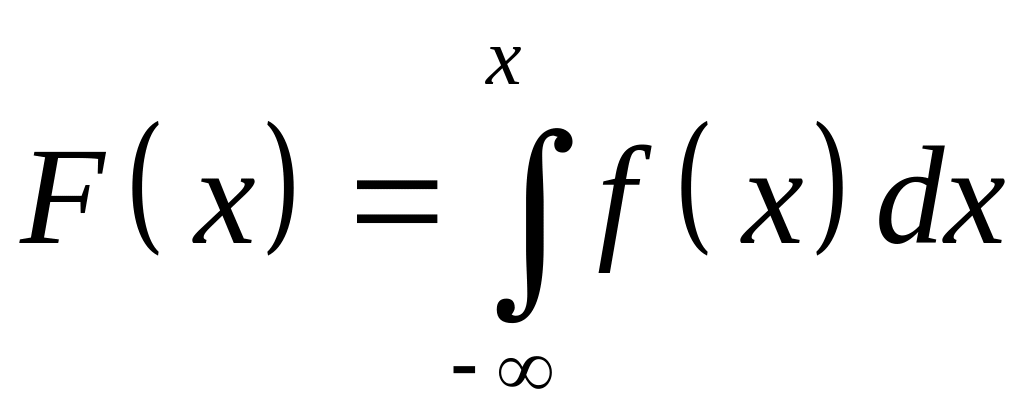 .
.
Интеграл в бесконечных пределах от плотности распределения равен единице (свойство нормированности):
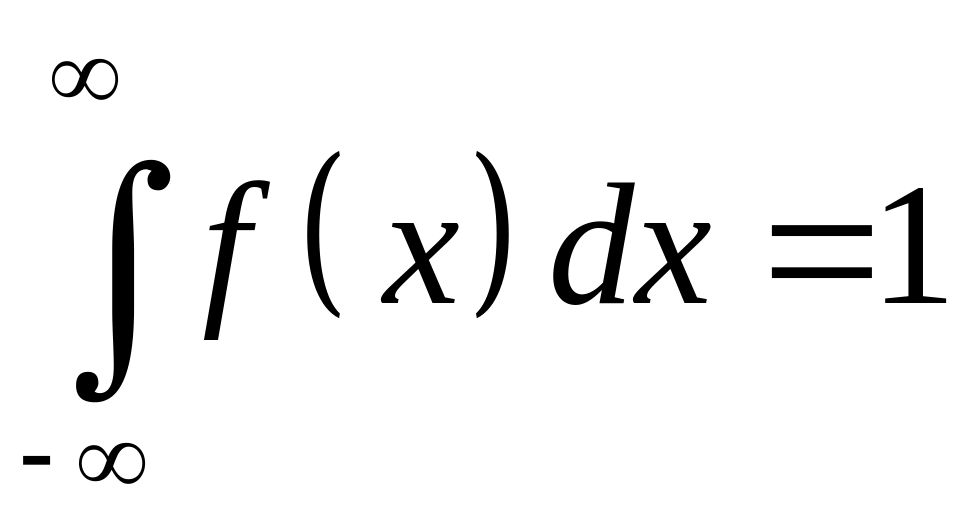 .
.
Замечание. Если функция не удовлетворяет свойству 4, то она не может быть плотностью распределения какой-либо случайной величины.
Числовые характеристики нсв
Математическое
ожидание для НСВ,
все значения которой принадлежат отрезку
![]() определяется
формулой:
определяется
формулой:
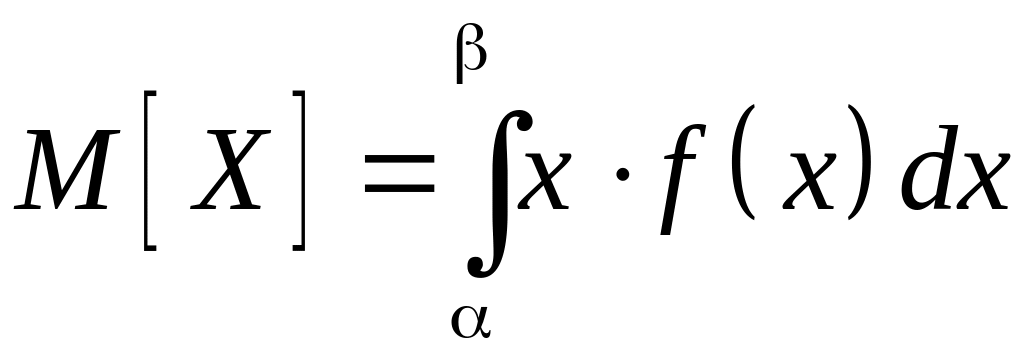 .
.
Если
все значения непрерывной случайной
величины принадлежат промежутку
![]() ,
то математическое ожидание определяется
формулой:
,
то математическое ожидание определяется
формулой:
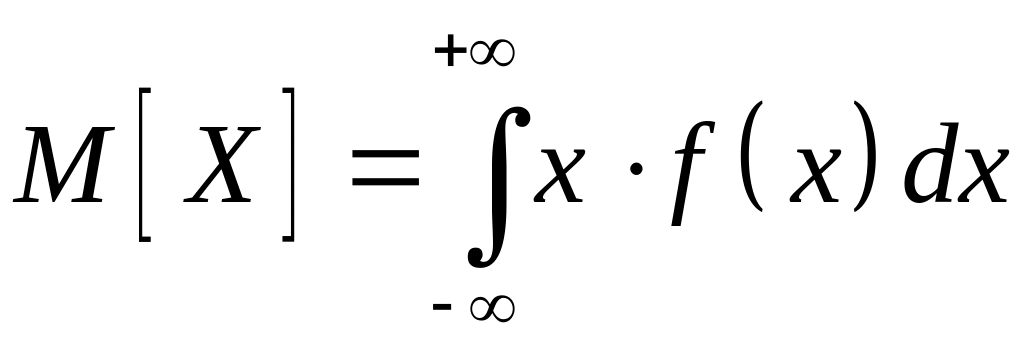 ,
,
если несобственный интеграл сходится абсолютно
Дисперсия НСВ, все значения которой принадлежат отрезку , определяется формулой
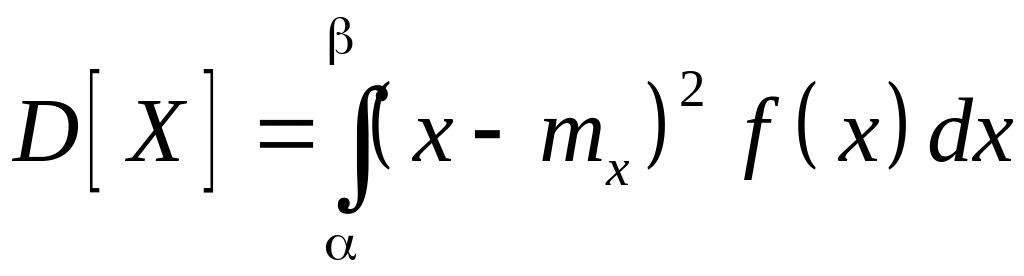 .
.
Если непрерывная случайная величина принимает значения, принадлежащие промежутку , то ее дисперсия определяется формулой
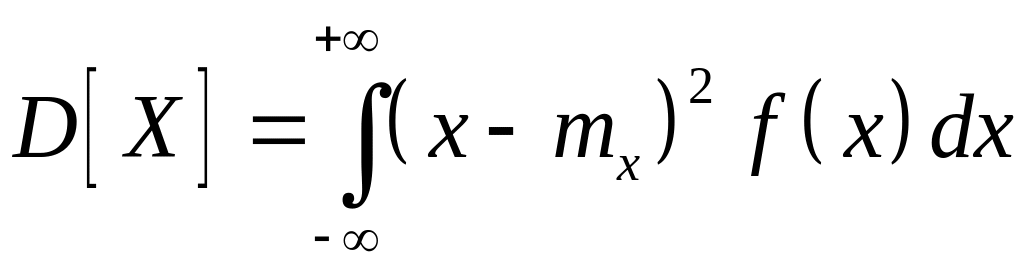 ,
,
если несобственный интеграл сходится абсолютно.
Среднее квадратическое отклонение случайной величины находится по формуле
.
Пример
Плотность распределения непрерывной случайной величины Х имеет вид
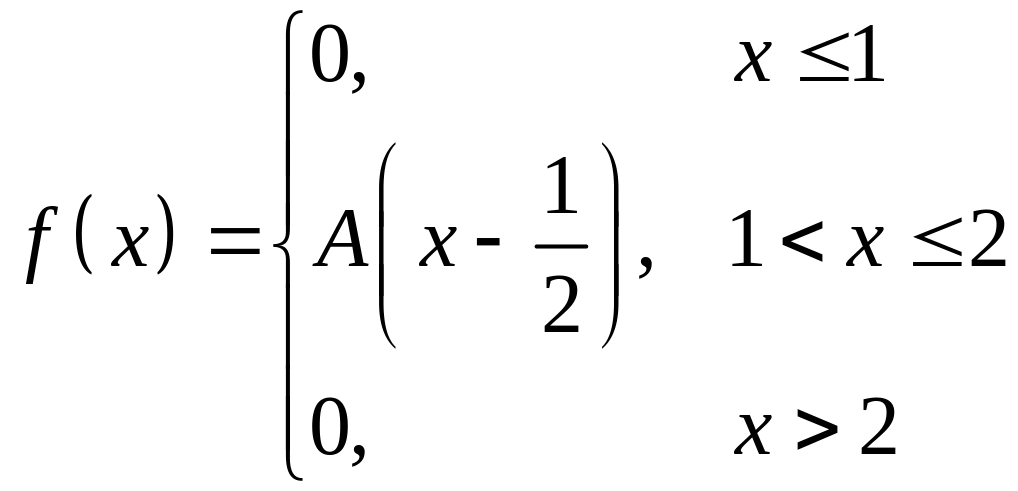 .
.
Найти:
параметр А,
функцию распределения
,
вероятность попадания случайной величины
Х
в интервал
![]() ,
математическое ожидание
,
математическое ожидание
![]() и дисперсию
и дисперсию
![]() .
.
Решение
Для определения
значения А
воспользуемся условием
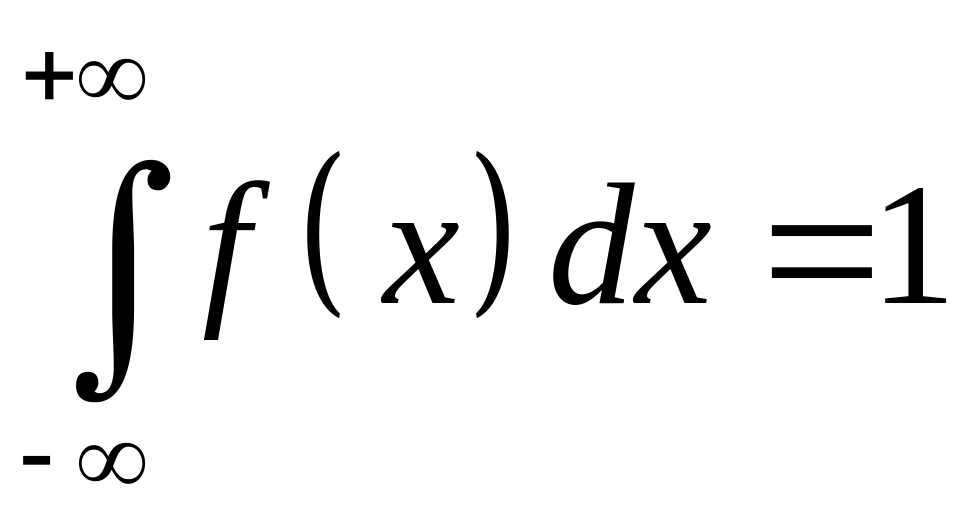 .
Вычислим интеграл
.
Вычислим интеграл
 ,
,
плотность распределения случайной величины Х примет вид
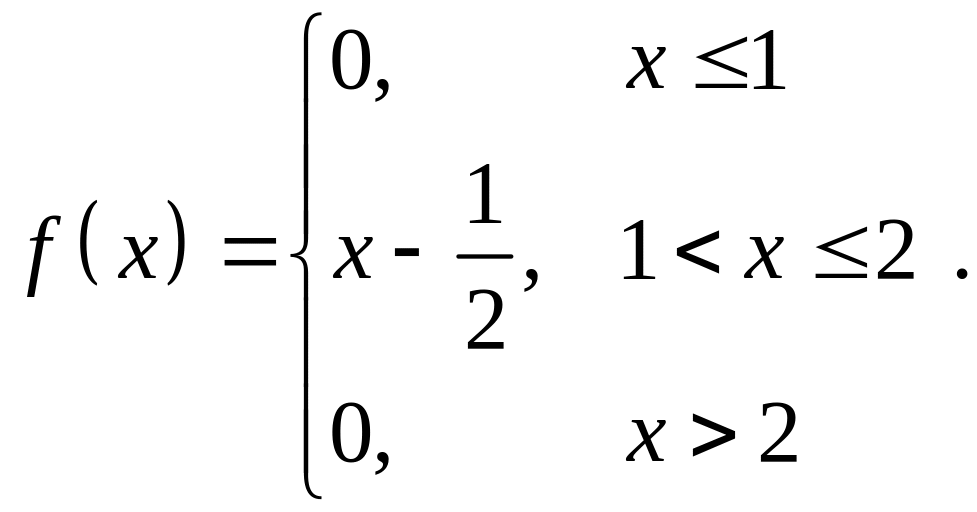
Для того, чтобы найти функцию распределения , воспользуемся формулой .
При
![]() получаем
получаем
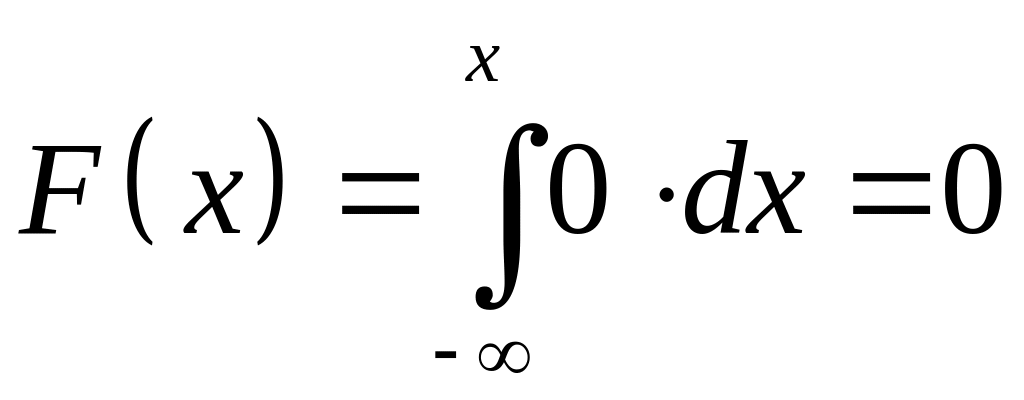 ,
,
при
![]() находим
находим
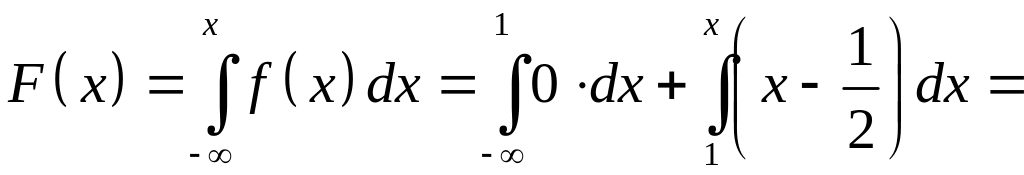
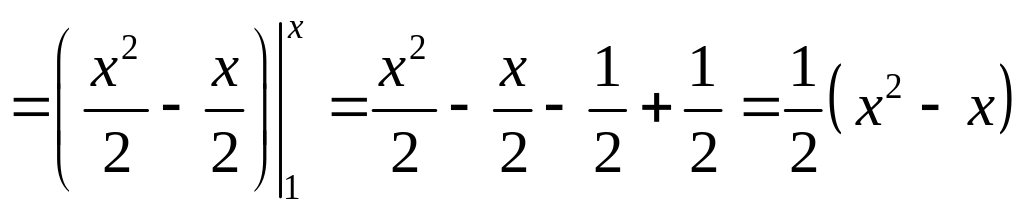 ,
,
при
![]() :
:
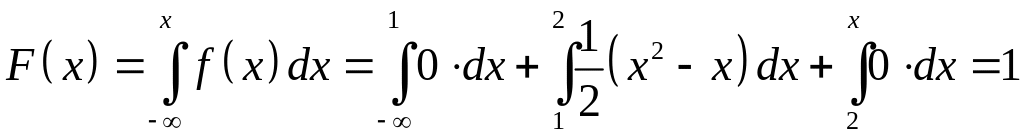 .
.
Таким образом, искомая функция распределения имеет вид

Вероятность попадания СВ Х в интервал найдем по формуле , она будет равна
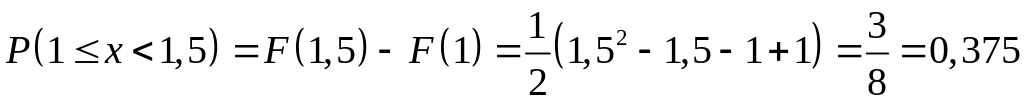 .
.
Математическое ожидание находим по формуле :
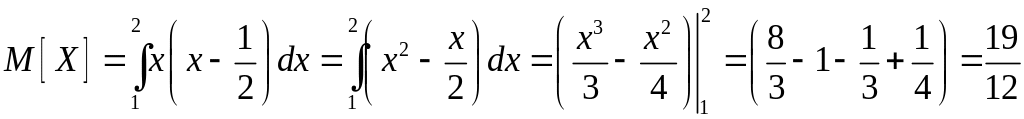 .
.
Дисперсию найдем по формуле :
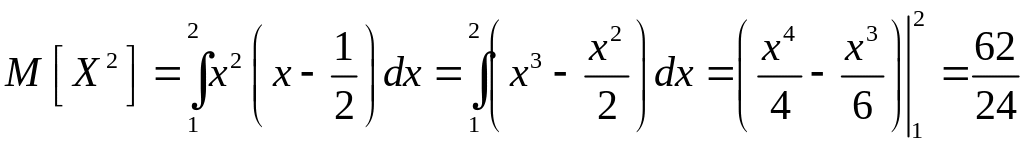 ,
,
тогда
 .
.
Контрольная работа № 6. Элементы математической статистики
Результаты измерений некоторой физической величины представлены в таблице:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
4 |
7 |
13 |
|
|
16 |
6 |
3 |
где i
– номер интервала,
![]() – границы интервала,
– границы интервала,
![]() ,
,
![]() ,
– частота.
,
– частота.
6.1.1. Найти функцию
распределения выборки
![]() и построить ее график.
и построить ее график.
6.1.2. Построить гистограмму относительных частот.
6.1.3. Найти числовые
характеристики выборки: выборочное
среднее
![]() и исправленную выборочную дисперсию
и исправленную выборочную дисперсию
![]() .
.
6.1.4. Используя
функцию Лапласа, построить доверительный
интервал для математического ожидания,
соответствующий доверительной вероятности
![]() .
.
6.1.5. С помощью
критерия
![]() (Пирсона) проверить гипотезу о нормальном
распределении генеральной совокупности
при уровне значимости
(Пирсона) проверить гипотезу о нормальном
распределении генеральной совокупности
при уровне значимости
![]() .
.
Двумерная выборка результатов совместных измерений признаков х и у объемом
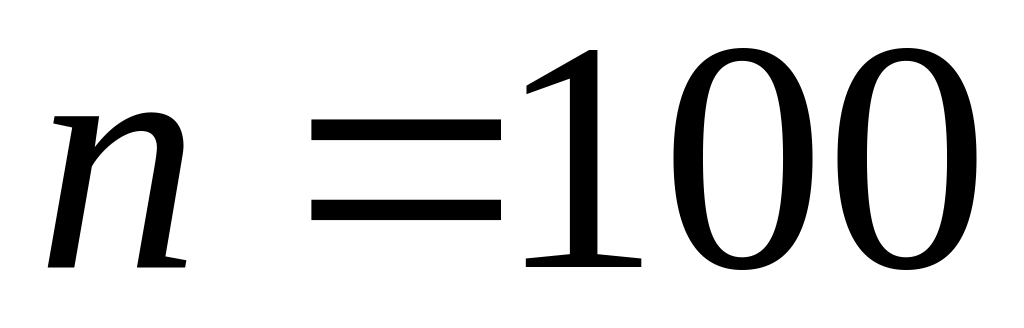 измерений задана корреляционной
таблицей:
измерений задана корреляционной
таблицей:
|
|
|
|
|
|
|
|
2 |
3 |
– |
– |
– |
5 |
|
3 |
8 |
2 |
– |
– |
13 |
|
– |
|
|
– |
– |
|
|
– |
– |
|
|
– |
|
|
– |
– |
9 |
10 |
– |
19 |
|
– |
– |
3 |
6 |
1 |
10 |
|
– |
– |
– |
1 |
2 |
3 |
|
5 |
|
|
|
3 |
|
где
![]() ,
,
![]() .
.
6.2.1. Найти выборочные
средние
![]() и выборочные дисперсии
и выборочные дисперсии
![]() .
.
6.2.2. Построить
уравнение линии регрессии Y
на Х
в виде
![]() .
.
6.2.3. На графике
изобразить корреляционное поле, т.е.
нанести точки
![]() и построить прямую
.
и построить прямую
.
