5.4. Дискретные случайные величины

Случайной величиной (СВ) называется величина, которая в результате испытания (опыта) может принять то или иное значение, причем заранее неизвестно – какое именно.

Условимся обозначать случайные величины прописными буквами:

X, Y, Z,…,

а их возможные значения строчными буквами: .

Законом распределения СВ называют любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной.

Дискретная СВ (ДСВ) – это величина, множество возможных значений которой дискретно, т.е. состоит из отдельных, изолированных точек, которые можно записать в виде конечной или бесконечной последовательности. ДСВ принимает свои возможные значения с определенными вероятностями.

Рядом распределения ДСВ Х называется таблица, в верхней строке которой перечислены в порядке возрастания все возможные значения СВ Х: , а в нижней – вероятности этих значений: , где – вероятность того, что в результате опыта СВ Х примет значение .

Ряд распределения записывается в виде таблицы:

Х			…		…
р			…		…

Так как в одном испытании СВ принимает одно и только одно возможное значение, то события несовместны и образуют полную группу. Следовательно, сумма всех вероятностей, стоящих в нижней строке ряда распределения, равна 1:

.

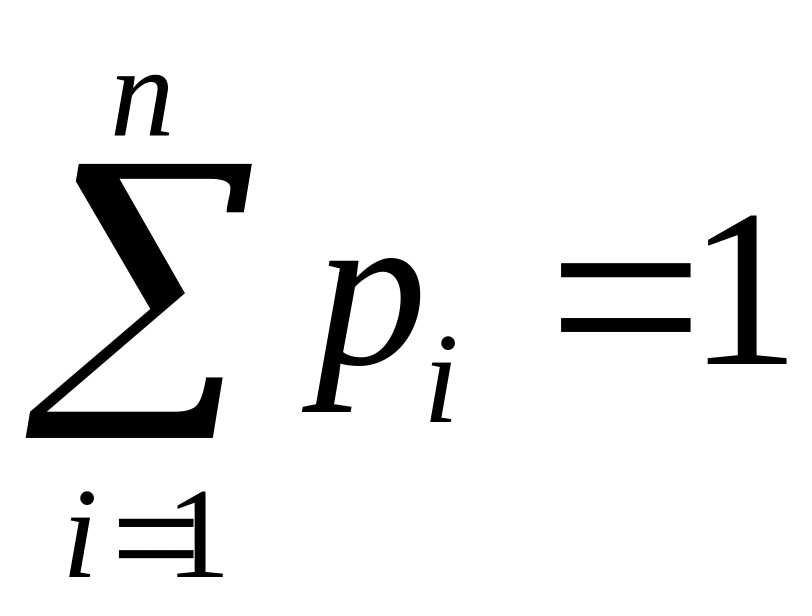Пусть ДСВ принимает бесконечную последовательность значений (множество значений ДСВ бесконечно, счетно). Тогда ряд распределения ДСВ примет вид:

Х			…		…		…
р			…		…		…

В этом случае ряд, составленный из чисел , сходится и его сумма равна единице.

Такой способ задания закона распределения ДСВ (в виде ряда распределения) называется табличным.

Графическое изображение ряда распределения называется многоугольником распределения. Строится он так: на оси абсцисс откладывают возможные значения СВ, на оси ординат – вероятности этих значений, таким образом, получаем точки . Полученные точки (пусть из будет четыре), для наглядности, соединяют отрезками прямых (рис. 1).

0

Рис. 1

Этот способ задания закона распределения ДСВ называют графическим.

Можно также задавать закон распределения ДСВ аналитически. Например, формула Бернулли: аналитически задает закон распределения, называемый биномиальным.

Функцией распределения СВ Х называется функция , , которая определяется формулой

(т.е. вероятность того, что СВ Х примет значение меньше наперед заданного значения х, где х любое вещественное число).

В случае ДСВ:

,

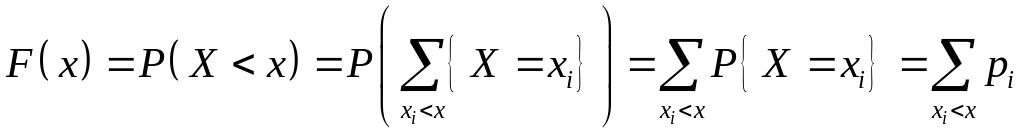где суммирование проводится по всем значениям , которые строго меньше х.

Функцию распределения называют интегральной функцией распределения или интегральным законом распределения.