4.5. Несобственные интегралы 1-го рода

Пусть дана функция , которая определена и непрерывна на промежутке . Пусть интеграл существует для любого конечного b и пусть

Предел интеграла при называется несобственным интегралом 1-го рода от функции на и обозначается символом .

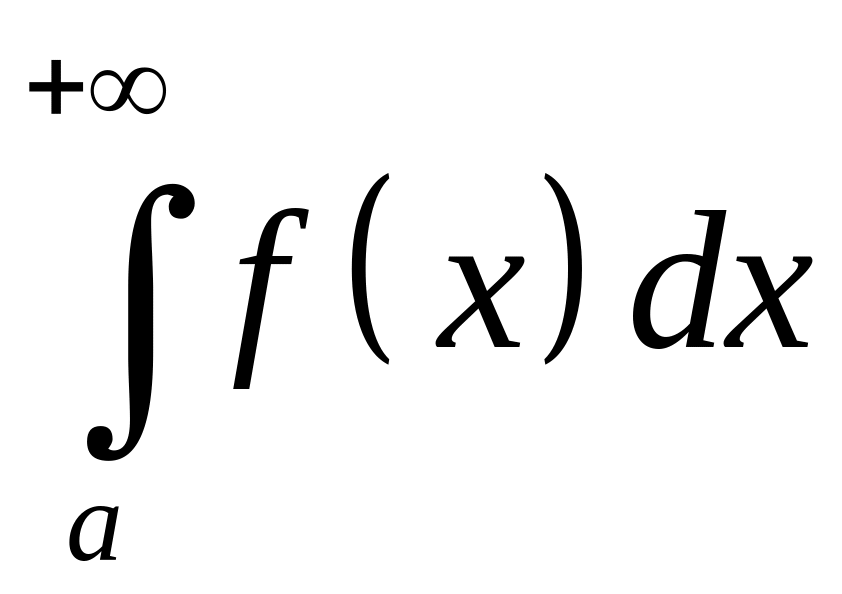Итак, .

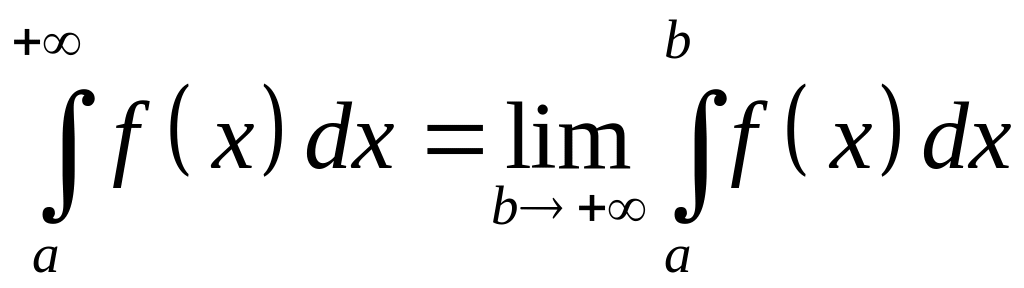Если этот предел конечен, то говорят, что интеграл сходится, а функцию называют интегрируемой на Если предел бесконечен или не существует, то про интеграл говорят, что он расходится.

Вычислить несобственный интеграл 1-го рода можно по определению.

Пример

Вычислить интеграл или установить его расходимость .

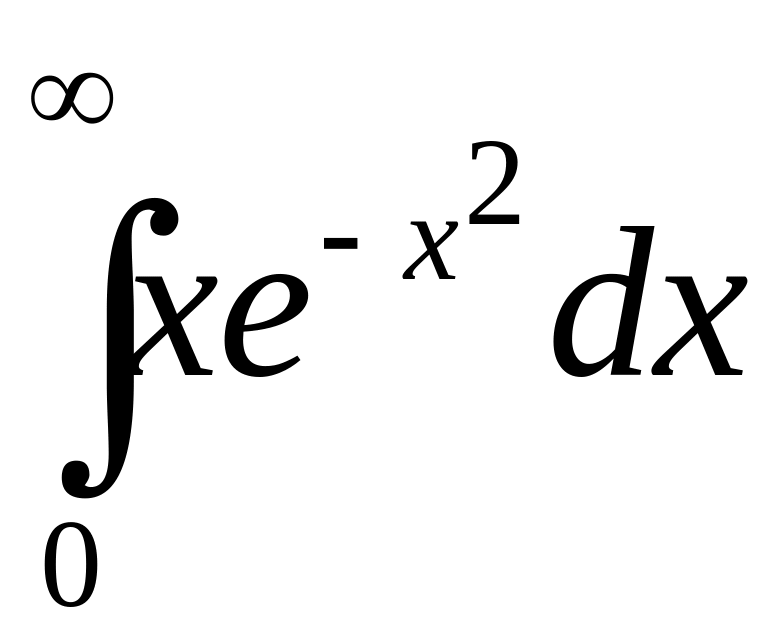Решение

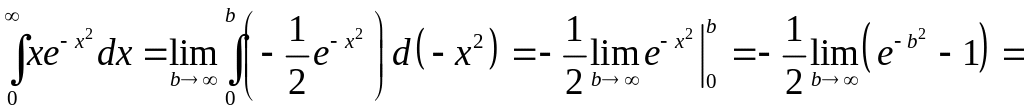
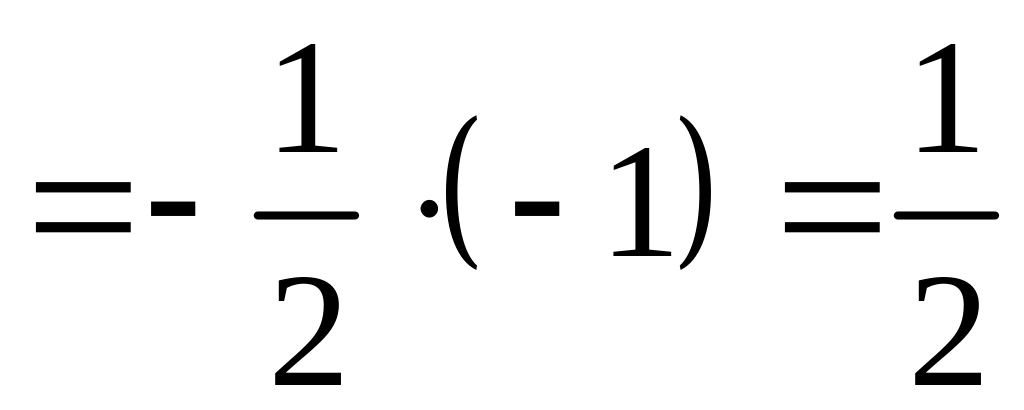, интеграл сходится.

Аналогично определяются еще два вида несобственных интегралов 1-го рода: 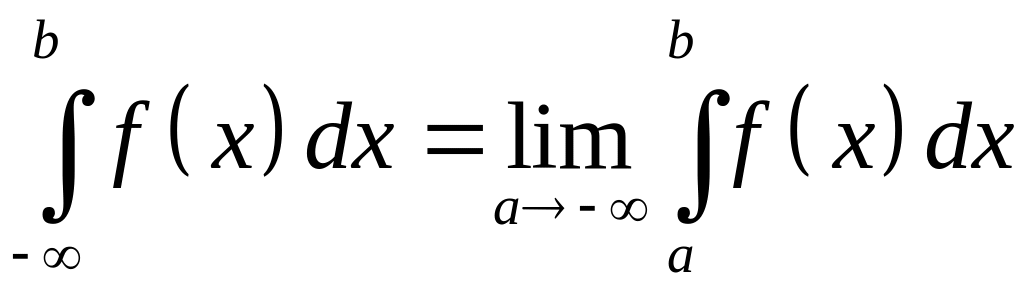и 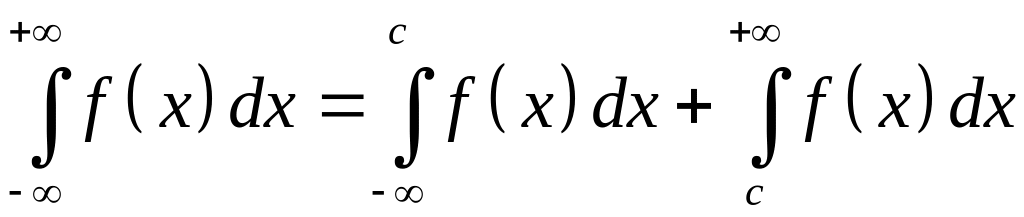, с – любое число.

Контрольная работа № 5. Элементы теории вероятностей

1. В коробке находится 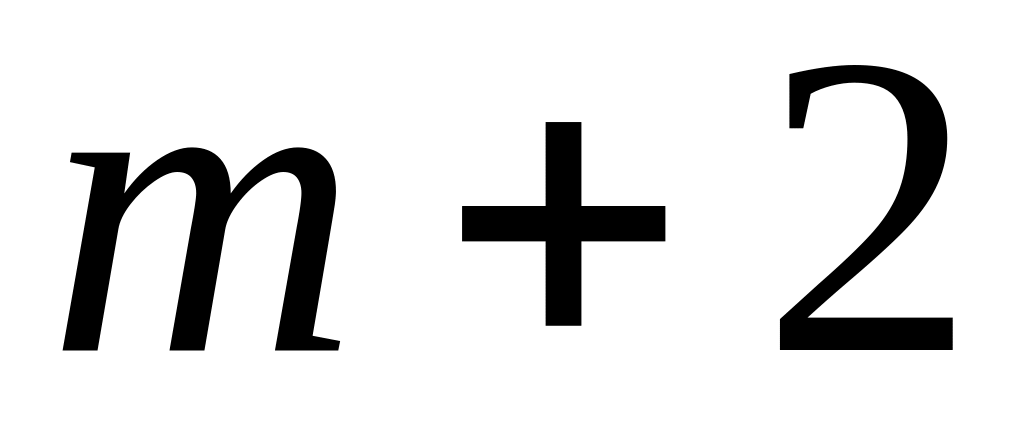синих, 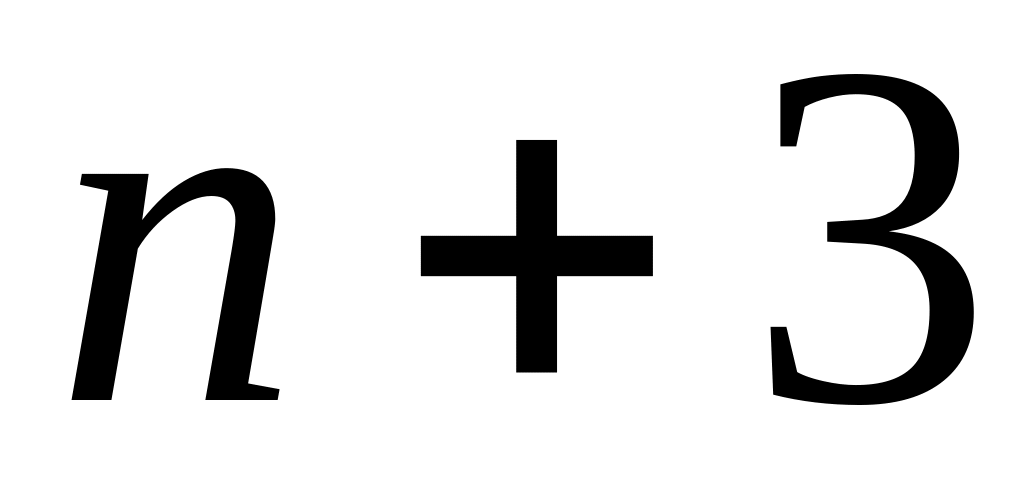красных и 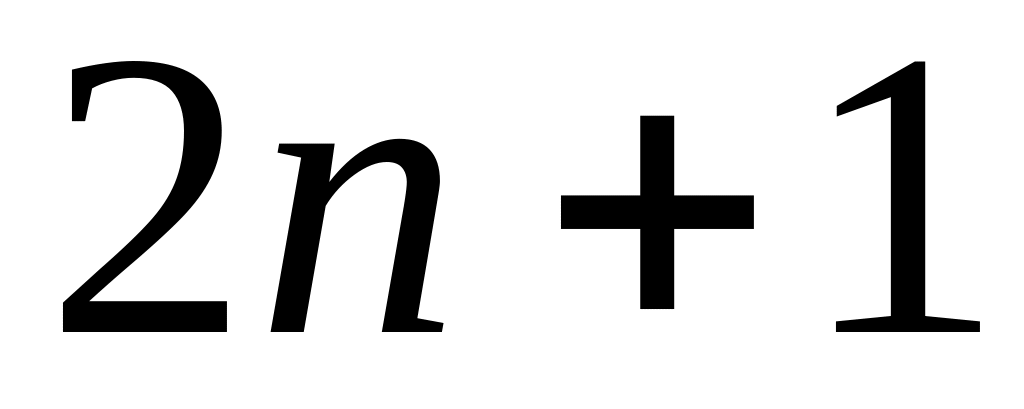зеленых карандашей. Одновременно вынимают 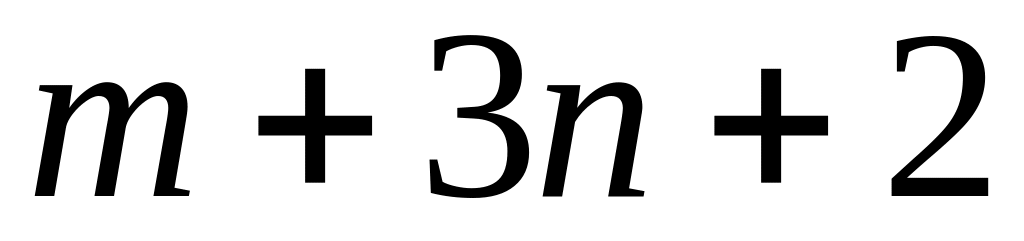карандашей. Найти вероятность того, что среди них будет 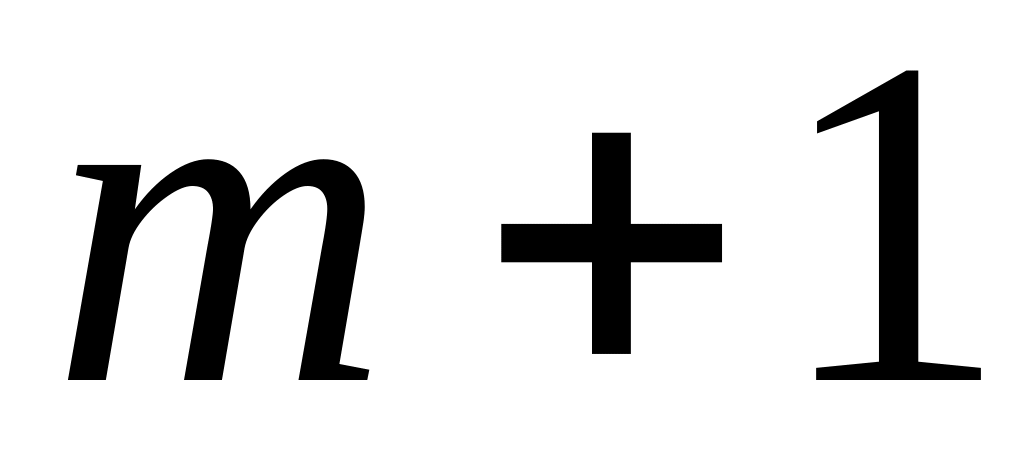синих и 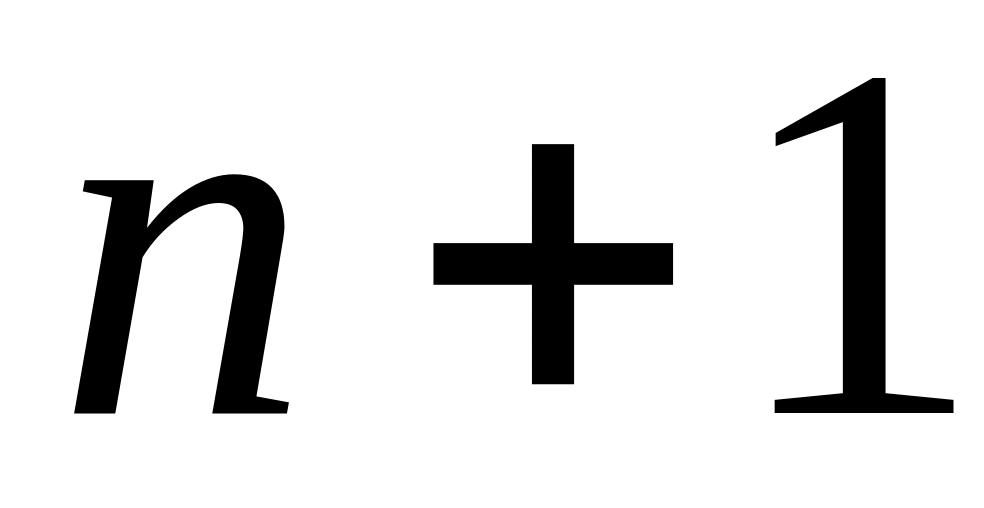красных карандашей.

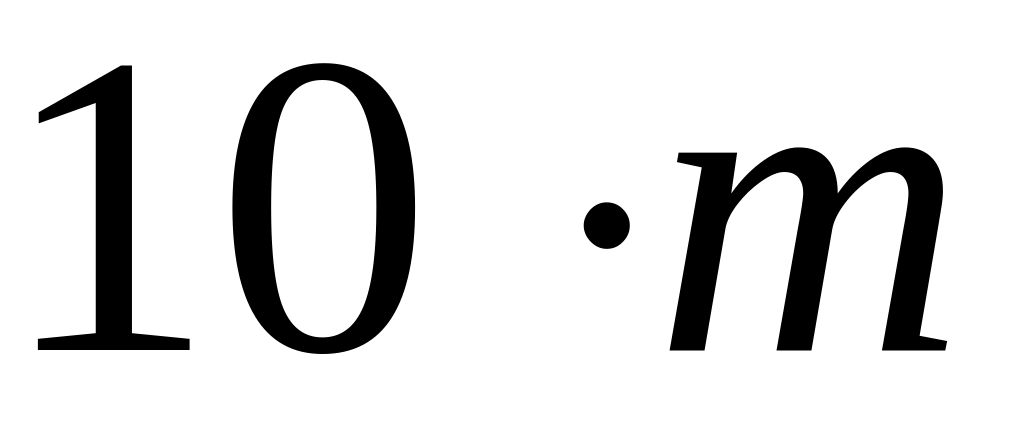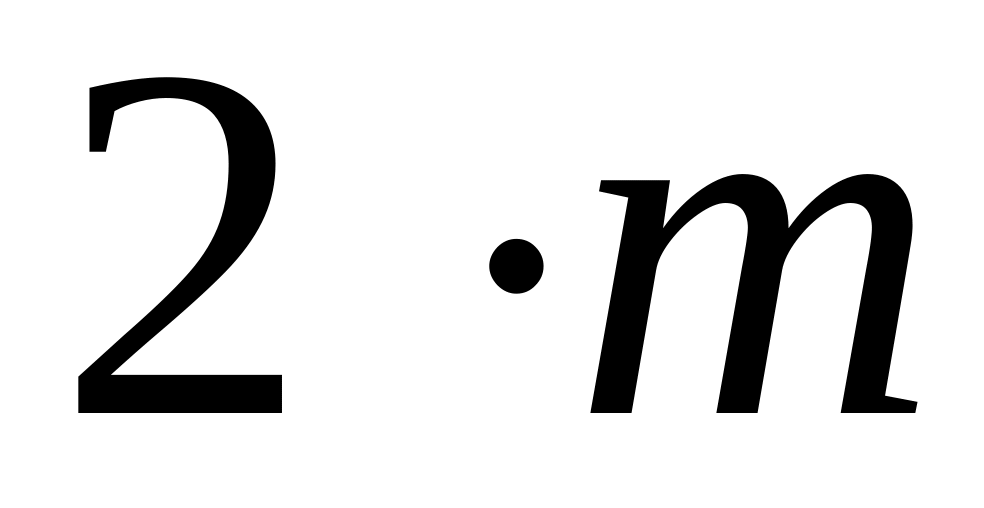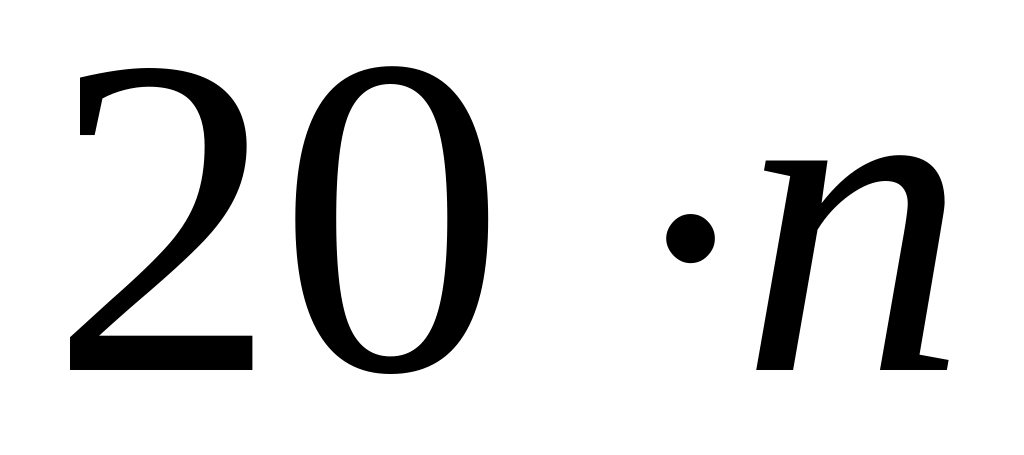2. На склад поступили ящиков, в которых содержится по годных деталей и бракованных и ящиков, в которых содержится по годных деталей и 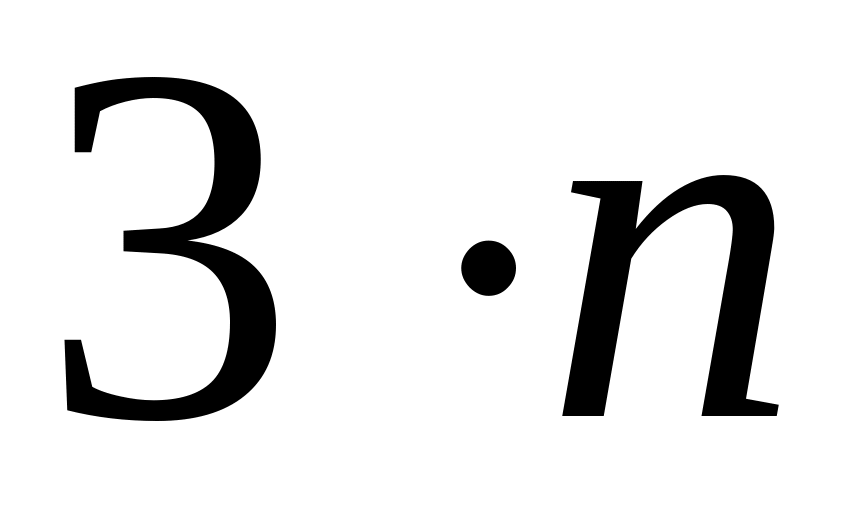бракованных. Наудачу выбирается ящик и из него наудачу извлекается деталь. Найти вероятность того, что вынутая деталь является годной.

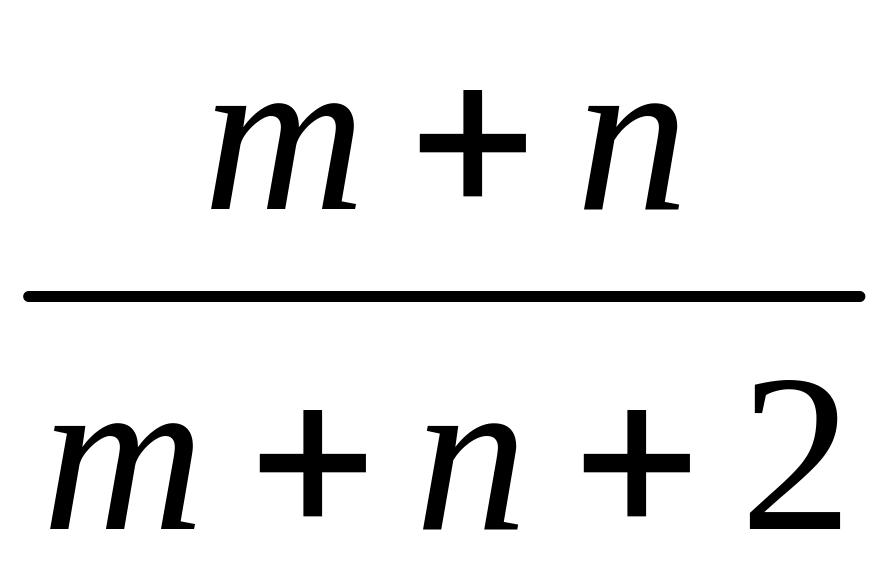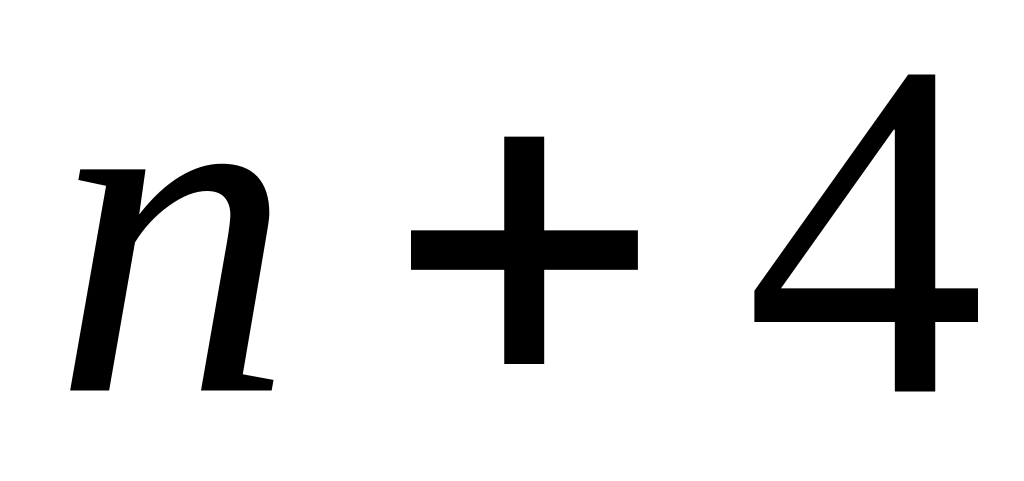3. Вероятность попадания стрелка в мишень при одном выстреле равна . Производится выстрела. Найти вероятность того, что он промахнется не более двух раз.

4. Ряд распределения дискретной случайной величины Х имеет вид:

			0
	0,2	0,1	0,2

Найти вероятности , если математическое ожидание . Построить многоугольник распределения. Найти функцию распределения и построить ее график. Вычислить дисперсию и среднее квадратическое отклонение.

5. Плотность распределения непрерывной случайной величины Х имеет вид:

.

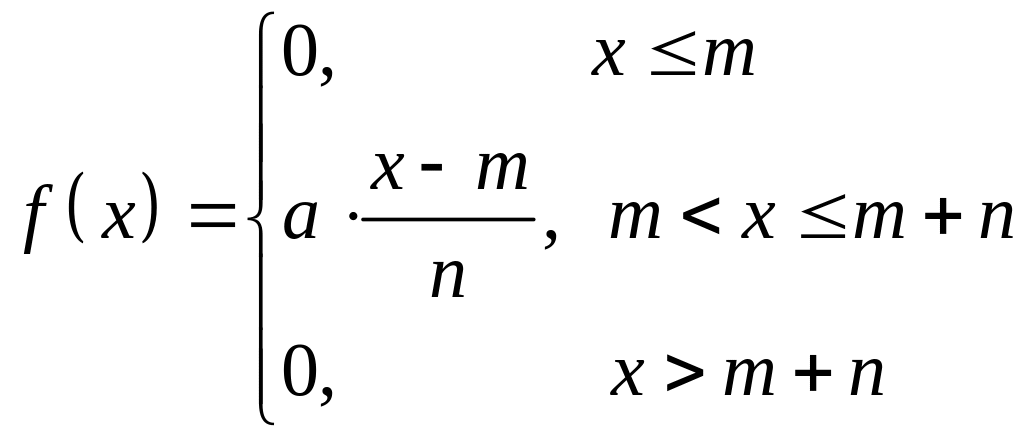Найти: а) параметр а;

б) функцию распределения ;

в) вероятность попадания случайной величины Х в интервал

;

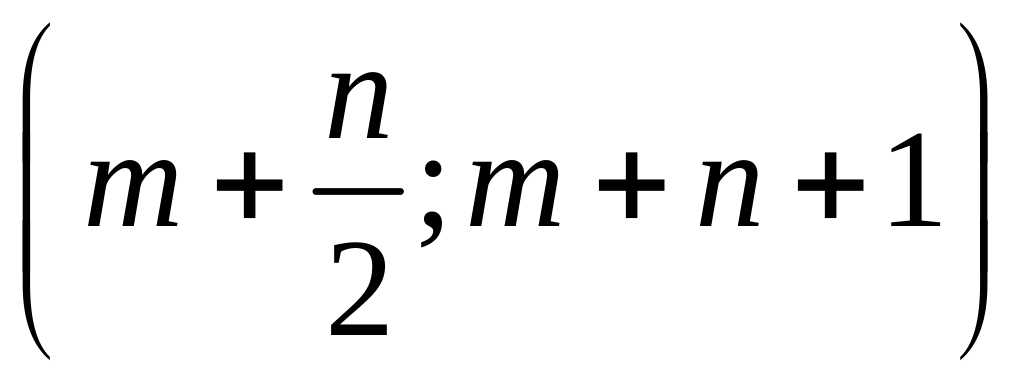г) математическое ожидание и дисперсию .

Краткие теоретические сведения для выполнения контрольной работы № 5 и решение типовых задач

5.1. Классическое определение вероятности

Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие.

Вероятность события А обозначается . В соответствии с определением

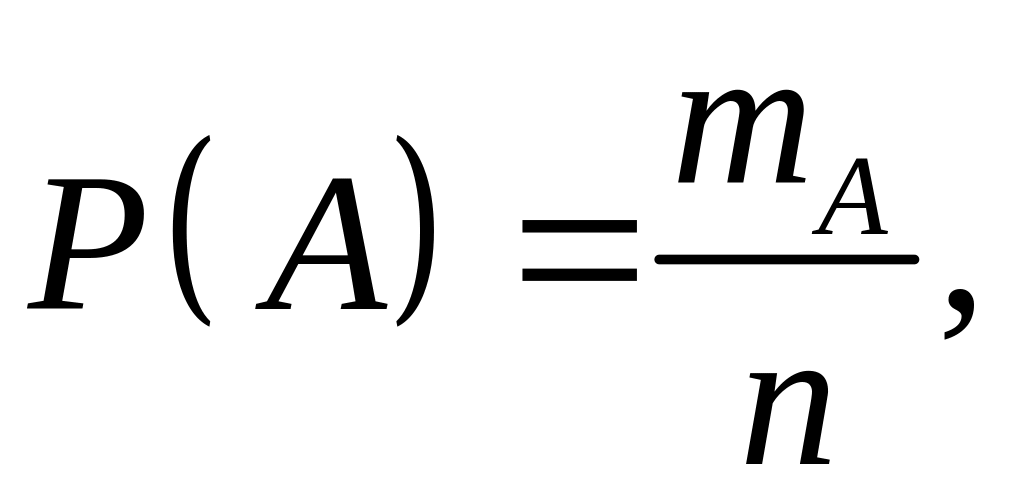
где – число элементарных исходов, благоприятствующих событию А, n – число всех равновозможных элементарных исходов опыта, образующих полную группу событий.

Это определение вероятности называют классическим. При вычислении вероятностей событий с использованием классического определения, могут быть использованы формулы комбинаторики.

Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов.

Число возможных перестановок из n элементов обозначают через , это число равно n!:

где по определению полагают, что

Размещениями называют множества, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.

Число всевозможных размещений определяется формулой

,

или

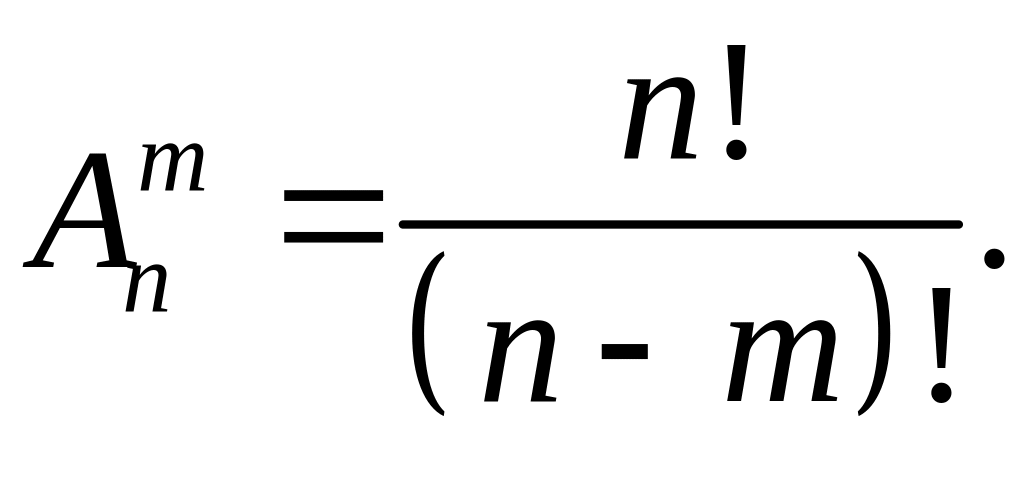
Сочетаниями из n различных элементов по m называются множества, содержащие m элементов из числа n заданных, и которые отличаются хотя бы одним элементом.

Число сочетаний из n элементов по m определяется формулой

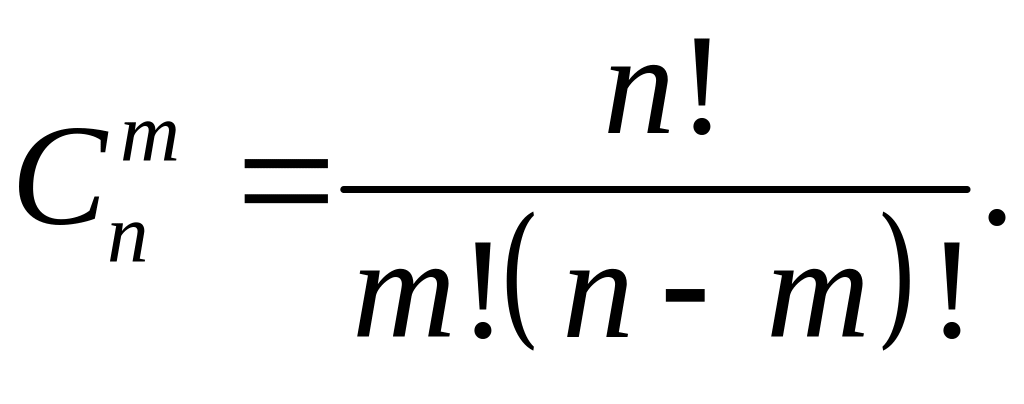
Число перестановок, размещений и сочетаний связаны равенством

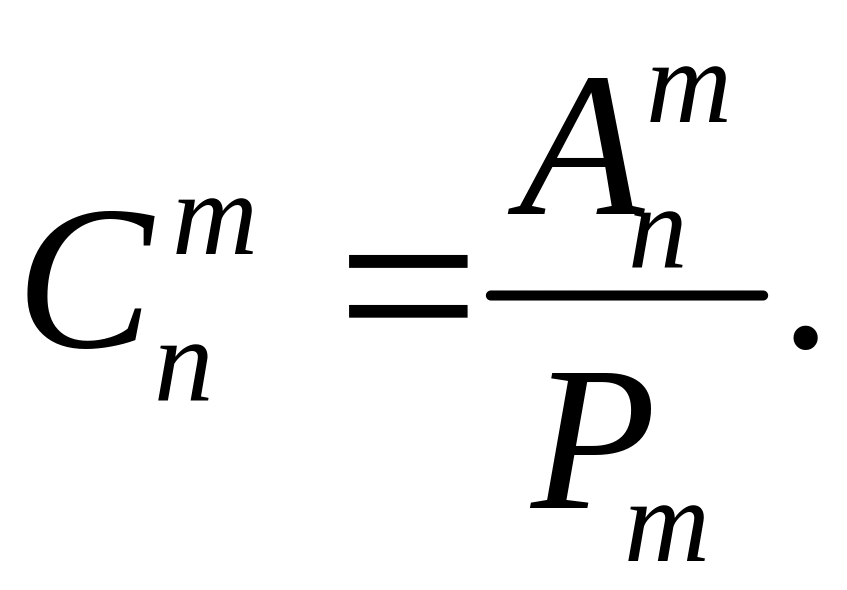
В приведенных формулах предполагалось, что все n элементов различны.

При решении задач комбинаторики используют следующие правила.

Правило суммы. Если некоторый объект А может быть выбран из множества объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно способами.

Правило произведения. Если объект А можно выбрать из множества объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана способами.

Пример 1

В ящике находятся 15 красных, 9 синих и 6 зеленых шаров. Наудачу выбирают 6 шаров. Какова вероятность того, что вынуты 1 зеленый, 2 синих и 3 красных шара (событие А)?

Решение

В ящике всего 30 шаров. При данном испытании число всех равновозможных элементарных исходов будет . Подсчитаем число элементарных исходов, благоприятствующих событию А. Три красных шара из 15 можно выбрать способами, два синих шара из 9 можно выбрать способами, один зеленый из 6 – способами. Следовательно (в силу принципа произведения в комбинаторике), число исходов, благоприятствующих событию А, будет .

По формуле 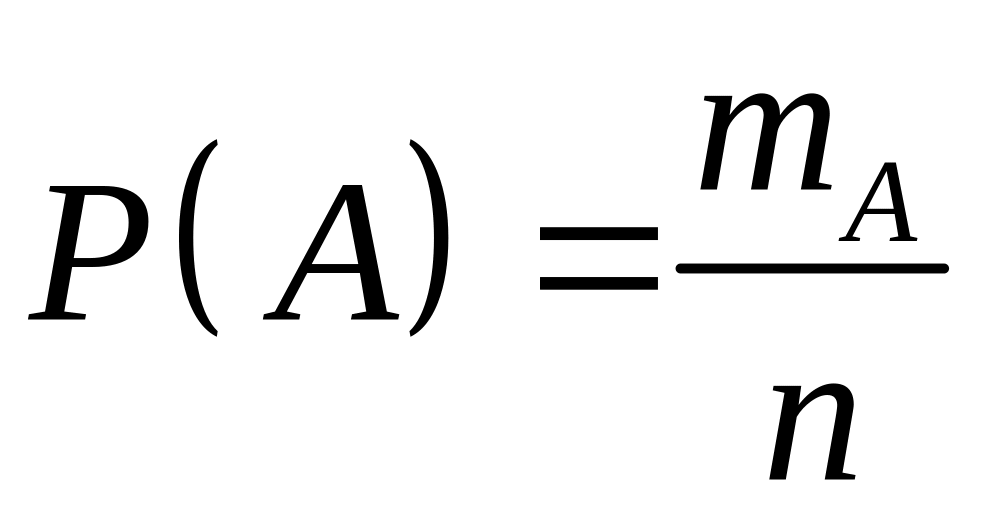находим искомую вероятность

.

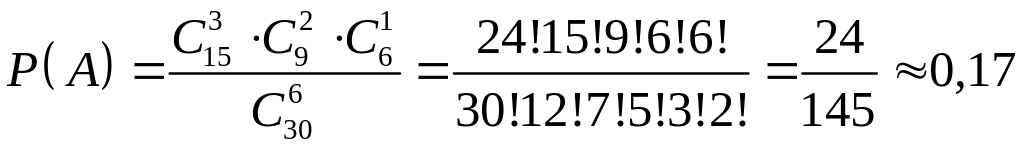Пример 2

На пяти одинаковых карточках написаны буквы И, К, М, Н, С. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность того, что получится слово МИНСК?

Решение

Из пяти различных элементов можно составить перестановок

.

Значит, всего равновозможных исходов будет 120, а благоприятствующих данному событию – только один. Следовательно,

.

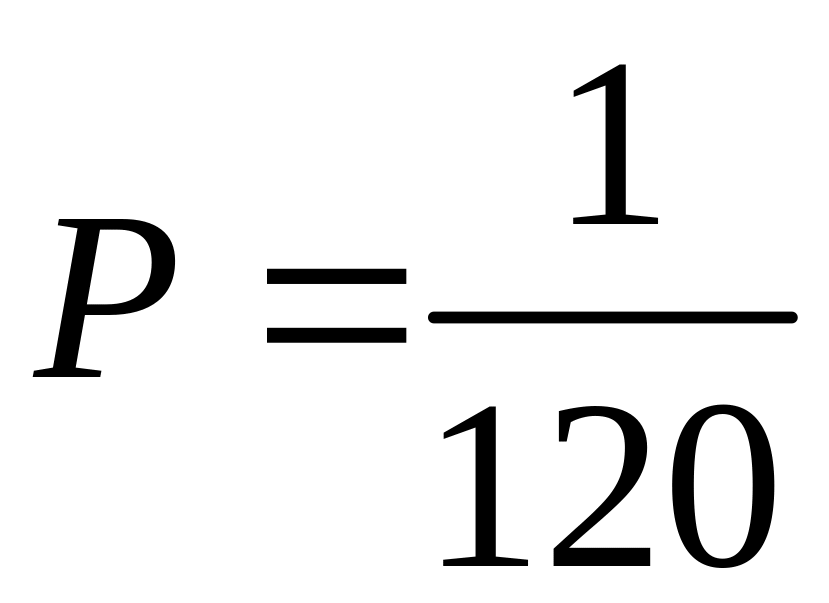Пример 3

Набирая номер телефона, абонент забыл последние три цифры и помнил лишь, что эти цифры различные. Найти вероятность того, что набраны нужные цифры.

Решение

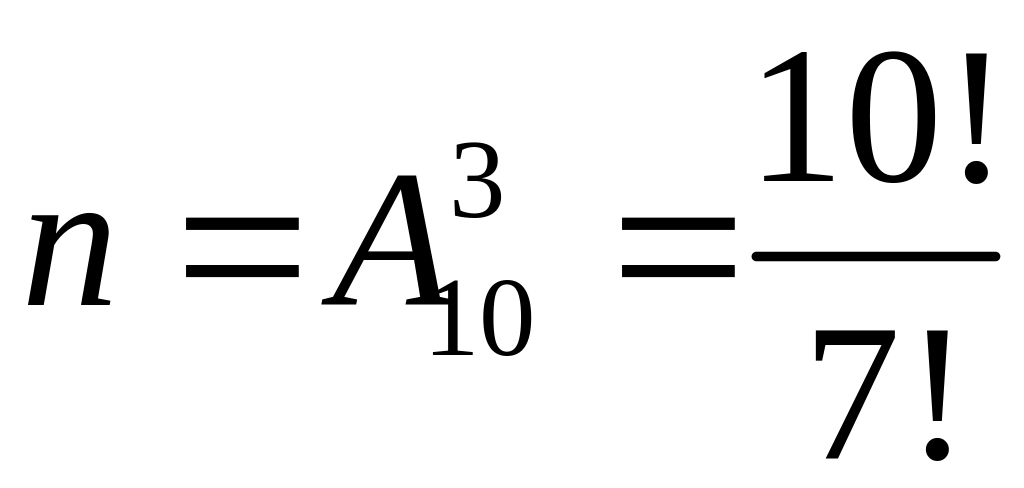Событие А – набраны три нужные цифры. Вероятность , – число исходов, благоприятствующих событию А, – число всех возможных вариантов набора, поэтому искомая вероятность

.
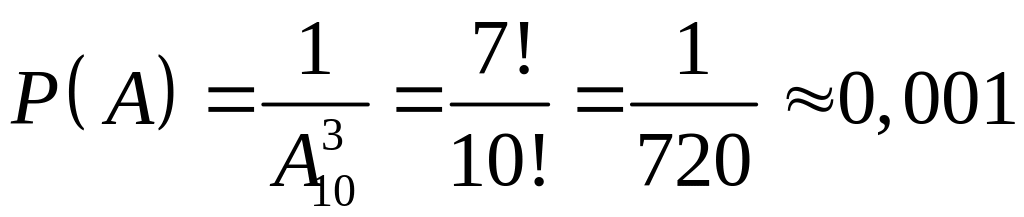